Важные примеры измеримых множеств.

Теорема 1. Если, тогда график функции- является измеримым множеством в, имеет площадь, равную нулю.

Доказательство:

Рассмотрим криволинейную трапецию, соответствующую этой функции на отрезке . Пусть у нас сначалана, тогда мы получаем криволинейную трапецию, а она измерима (было доказано в первом семестре), следовательно мера ее границы.

Аналогично, если функция знакопеременна, так как она непрерывна, то ограничена снизу некоторой константой , тогда мы опустим ось абсцисс до прямойи снова получим криволинейную трапецию.

Следствие 1.Если на плоскости задана непрерывная кривая, однозначно проецируемая на какую-либо прямую, то ее мера равна нулю.

Пусть у нас задана непрерывная кривая, однозначно проецируемая на некоторую прямую, тогда мы можем сделать так, чтобы эта кривая находилась по одну сторону от этой прямой. Тогда мы из этой прямой делаем ось абсцисс и восстанавливаем ось ординат, таким образом, мы попадаем в условие теоремы1.

Следствие 2.Если кривая на плоскости состоит из ограниченных участков, однозначно проектируемых на какие-либо прямые и их число конечно, то кривая имеет меру 0.

Следствие 3.Множество, ограниченное на плоскости кривыми из следствия 2 является измеримым.

Мы уже доказывали, что если мера границы множества равна нулю, то оно является измеримым.

Пример. ,- множество, ограниченное этими кривыми, измеримо.

Теорема 2. (Мера поверхности в ).

Пусть задана поверхность , с помощью уравнения, где- ограниченное, замкнутое, а, тогда

Доказательство:

Мы должны доказать, что это множество можно поместить в фигуру как угодно малого объема.

Поместим ограниченное множество в прямоугольник, разобьемначастей, то есть каждую его сторону разделим начастей, тогда

, где- некоторая константа.

Обозначим ,, тогда, так как функция, непрерывная на замкнутом ограниченном множестве, является равномерно непрерывной,

при.

То есть мы разбили на кусочки прямоугольник в плоскости . Это разбиение на плоскости порождает и разбиение поверхности

Далее пусть - участок поверхности над, то есть

.

Тогда

, следовательно.

Теорема 3. (Мера поверхности в ).

Пусть - поверхность в.

..

Тогда если - непрерывно дифференцируемы на, то

Доказательство:

Разобьем сторону начастей, тогда саммы разобьем начастей.

,

.

,

при.

Следствие 1.Если- непрерывно дифференцируемы на, где- замкнутое, ограниченное, тогда.

Следствие 2.Еслиимеет границу, состоящую из конечного числа поверхностей, удовлетворяющих условию следствия 1, то оно измеримо.

Кратные интегралы. Понятие функции, интегрируемой по Жордану.

Пусть задано множество , везде далее оно измеримо, задана также функцияна.

1. Введем разбиение на измеримые подмножества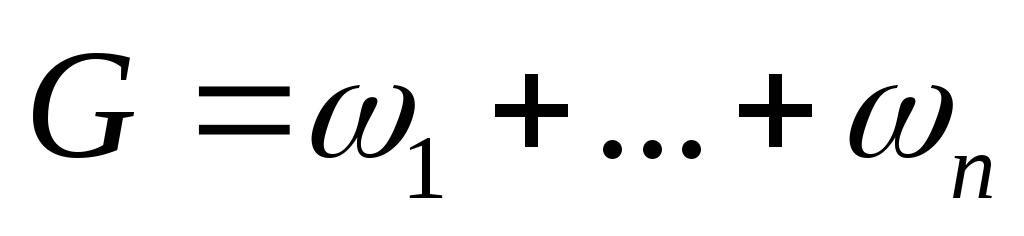.могут пересекаться разве только по границе.

2. 

3. Возьмем любую точку , составим интегральную сумму

4. Если существует , то этот предел называется кратным интегралом отпои обозначается

Следствие 1. Пусть задана- ограниченная на- измеримом множестве, тогда, если найдется последовательность разбиенийс мелкостьюприи существуетразбиения, тоинтегрируема на множествеи ее интеграл.

Это следствие отличается от определения интеграла по Гейне. В определении интеграла по Гейне у нас было для любой последовательности разбиений, с мелкостью , здесь последовательность только одна.

Доказательство:

Нам нужно доказать, что если у нас есть одна последовательность, то для любой будет выполняться все тоже самое. Раз это выполняется для одной последовательности, то , а раз нашлось одно такоеk, то по основной теоремебудет выполняться это же неравенство и функция будет интегрируема. Таким образом, можно говорить не о произвольных разбиениях, а о равномерных, например, проводить через каждыеh плоскости, только чтобы сторона полученногоn-мерного параллелепипеда стремилась к нулю.

Следствие 2.Если задано- измеримое множество, то, гдевключает в себя те, для которыхне пересекается с границей.

Доказательство.

Схема доказательства такая же, как и в основной теореме.

Раз множество измеримо, то .

Тогда мы можем ее поместить в некоторое множество как угодно маленькой меры.

Далее, отступим отна.

Построили фигуру.

.

Разбиваем нашу сумму на две . Так как у наси оно пересекается с границей, то. А, то есть мы можем сделатькак угодно малой (функция ограничена). Но тогда.

То есть, в интегральных суммах мы можем не считать области, примыкающие к границе.

Следствие доказано.