Лекция 10 Замена переменных в кратном интеграле. Преобразование элемента площади.

Лемма Бореля.

Из всякого открытого покрытия замкнутого ограниченного множества можно извлечь конечное подпокрытие.

Система множеств . Тогда найдутся, что.

Теорема. О преобразовании элемента площади.

- измеримое, замкнутое.

Преобразование .

,- непрерывно дифференцируемы на.

взаимнооднозначно, кроме, может быть, точек границ.

. Тогда какой бы кубизмы не взялиэто уже не куб. И

, где- произвольная точка, а- общий модуль непрерывности функций

Доказательство.

Возьмем произвольное . И рассмотрим квадрат.

Пусть .

, тогда по теореме о среднем

Рассмотрим преобразование

- оно уже будет линейным, так как мы зафиксировали производные в точке.

Аналогично для других точек.

- справедлива для произвольногоn.

Рассмотрим разность образов одной и той же точки при разных преобразованиях - расстояние между образами точек не превосходит вот этого.

Построим шары с центром в каждой точке границы радиусом . Обозначим через. Тогда.

Тогда мы получаем, что .

Из множества eпо лемме Бореля можно выделить конечное подпокрытие. А. Отсюда

Далее, - это, а в формулировке теоремывычислен в произвольной точке.

Их разница: . То есть, мы можем написать.

Подставим:

Пусть поверхность задана параметрически.

Функции ,,непрерывно дифференцируемы.

,.

- можно сказать, что частные производные одновременно не обращаются в нуль, тогда площадь

Эту формулу можно записать короче.

Рассмотрим

Обозначим ,

Пример.Площадь поверхности шара радиуса .

1. Сначала пусть шар задан в явном виде.

,

Тогда площадь всей сферы равна .

2. Сфера задана параметрически.

.

Лекция 11 Физические приложения.

1.Вычисление массы.

Пусть измеримое (тело) или(пластина).

И задана функция плотности - неотрицательна, непрерывна.

Будем считать, что масса сосредоточена в одной точке . Тогда.

При

2. Момент инерции.

Относительно начала координат. Точно также разбиваем, сосредотачиваем массу кусочка в одной точке, тогда общий момент инерции будет равен - сумме моментов инерции отдельных кусочков.

,.

- в случае, если функция плотности непрерывна.

, где- точка, прямая, плоскость.

2. Координаты центра масс.

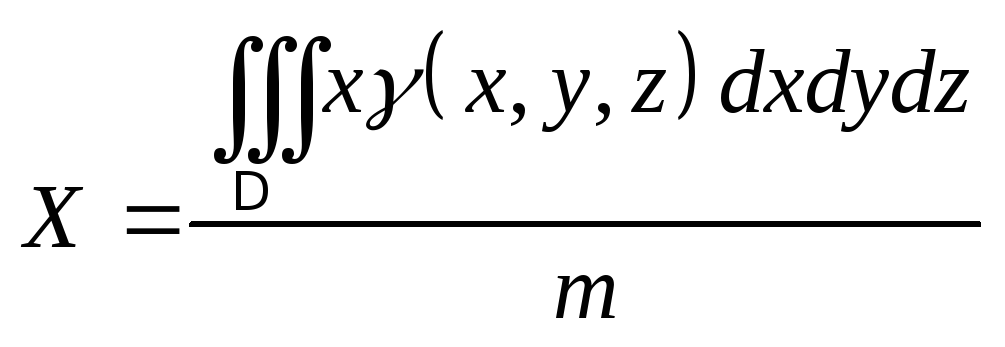, выражение, стоящее в числителе, называется статическим моментом.

Лекция 12 Несобственные интегралы кратные интегралы

Пусть - конечная область, рассмотрим точку, обозначим через, предположим, чтотакова, что- интегрируема, а в- неограничена.

Если - бесконечная область, тогда,,- интегрируема на.

Если существует- несобственный интеграл.

Обратим внимание на разность между этим определением и тем, что у нас уже было. Интеграл Римана можно рассматривать и как однократный интеграл. И для конечных областей понятия интеграла Римана и однократного кратного интеграла совпадают. Посмотрим, совпадают ли эти понятия для несобственных интегралов.

В смысле несобственных интеграла Римана: - расходится.

Всмысле этого определения мы точку, в которой у нас особенность мы окружаем шариком радиуса. Тогда рассматриваем предел. То есть, в смысле этого определения этот интеграл существует.

Свойства.

Критерий Коши.

или.

Вместо шаров можно рассматривать n-мерные кубы.

Все свойства несобственных интегралов сохраняются.