Криволинейные интегралы второго рода.

Определение.

Пусть дана гладкая ориентированная кривая, то есть зафиксируем у этой кривой непрерывное поле касательных. На кривой задано непрерывное поле. Пусть в каждой точке этой кривой задано векторное поле .

Точно так же разобьем эту кривую.

Возьмем произвольную точку , и рассмотрим скалярное произведение, где- единичный вектор касательной. То есть, фактически мы зафиксировали направление движение.

Тогда, если существует , и он не зависит от способа разбиения и выбора точек, то он называется криволинейным интегралом второго рода и обозначается.

Физический смысл.

Пусть в каждой точке кривой - сила, тогда интеграл даст работу этой силы по перемещению материальной точки по дуге.

Свойства.

1. Аддитивное свойство.

2. Однородные для сложения и умножения на скаляр:

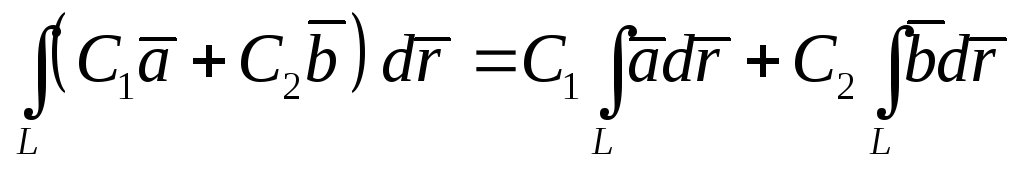
3) - так как направление касательных меняется на противоположную.

Вычисление и существование.

1й способ– через интеграл первого рода.

Если дана гладкая кривая ,,- возрастающие откисоответствует возрастанию параметра, тогдаи мы просто находим криволинейный интеграл первого рода..

2й способ.

Пример. Пусть задано векторное поле. Вычислим работу этого поля от (1;0) до

(-1;0)

1. по окружности: ,,.

2). По прямой.

,

Циркуляция векторного поля. Формула Грина.

- кусочно-гладкая, замкнутая.

Задано поле на этой кривой, зафиксируем ориентацию кривой соответственно внешней нормали.

- циркуляция вектора, иногда обозначается.

Область типа .

Область называется областью типа , если любая прямая, параллельная оси, проведенная через внутреннюю точку области, пересекает границу области ровно в двух точках.

Аналогично, область называется областью типа , если любая прямая, параллельная оси, проведенная через внутреннюю точку области, пересекает границу области ровно в двух точках.

Тогда область называется областью типа , если она типаи.

Теорема.Пусть- область типас гладкой границей, задано векторное полена, при этомнепрерывно и- непрерывные частные производные, тогда справедлива формула Грина

Доказательство.

Нашу область можно представить в виде ;. Рассмотрим:

.

Нашу область можно задать следующим образом:

.

, тогда

- знаки учитывают направление обхода. Вторую часть мы тоже доказали, теперь сложим эти два интеграла и получим формулу Грина.

Следствие: (обобщенная формула Грина).

Пусть- измеримая связная область, которую можно разбить на конечное число областей типа.- граница направленная в положительном направлении, назадано векторное поле, где

- непрерывны на., тогда справедлива формула Грина. Раз ее можно разбить на конечное число областей, давайте так и сделаем. (см. рис). Для каждой из этих областей формула Грина будет выполняться:. Внутренние границы входят в 2 участка, причем для одного участка она берется с плюсом, а для другого с минусом, то есть сумма криволинейных интегралов по внутренним участкам границы будет равна нулю.

Пример.

Вычислить по формуле Гринапо куску параболы.

Замкнем наш контур, тогда . Получаем:

Если , тогда. Из рисунка видно, что приращение радиус-вектора стремится к положению касательной.