Интегрируемость непрерывных функций.

Теорема.Функция, непрерывная на компактеинтегрируема на нем.

Доказательство.

- непрерывна, следовательно, она равномерно непрерывна на, то есть

при этом.

Рассмотрим разбиение ,, рассмотрим разность между верней и нижней суммами Дарбу.

- так как функция у нас непрерывна, то она достигает своего максимального и минимального значения.

,, тогда.

Из равномерной непрерывности получаем, что Умножим наи просуммируем.

.

Теорема доказана.

Следствие.Если- непрерывна на- компакте везде, за исключением множества меры 0,, но ограничена на, тоинтегрируема на.

Доказательство.

Здесь нужна теорема и следствие из предыдущего пункта. Мы сделаем как в следствии, мы можем говорить, что при каждом разбиении мы не учитываем множества, прилегающие к . Окружаем множество меры 0 фигурой маленькой площади и рассматриваем нашу функцию на оставшейся части. На оставшемся множестве функция будет интегрируема, а сумма по участкам, содержащимся внутри фигуры, будет стремиться к 0, потому как функция на этом множестве ограничена, а его мера стремится к нулю.

Значит все интегральные суммы, по всему будут стремиться к интегральным суммам без этих участков, а этот предел существует, потому что функция непрерывна.

Свойства кратных интегралов.

Теорема 1. Аддитивное свойство.

Если - интегрируема на- измеримом и- измеримые множества, которые пересекаются быть может только по границе, то- интегрируема наии.

И наоборот. (Доказательство в первом семестре).

Следствие.Пусть- интегрируема на, если,,ограничена на, тоинтегрируема наи.

Доказательство.

Следствие доказано.

Таким образом, понятие интеграла можно распространить на функции, определенные не на всем множестве, но везде, за исключением множества меры 0.

Теорема 2. Однородные свойства.

Если иинтегрируемы на, то

1)- интегрируема

2) - интегрируема.

3) - интегрируема

4) Если , то- интегрируема.

При этом выполняются равенства:

Теорема 3. Неравенства и теорема о среднем.

Пусть иинтегрируемы на- измеримом и- интегрируема на,,, тогда по теореме 2

Если ограничена на, то есть, то

.

Доказательство самостоятельно или пока я не соберусь…

Следствие:- связное измеримое замкнутое, ограниченное множество,- непрерывна на, следовательно интегрируема, тогда.

Доказательство.

Впредыдущей теореме возьмем в качестве, тогда. Надо теперь доказать, что этодостигается.

Можем рассмотреть функцию одной переменной

, а так как функцияу нас непрерывная (множество связное), то она принимает все промежуточные значения междуи, значит..

Доказано.

Упражнение.Доказать все, что не было доказано.

Вычисление кратных интегралов.

Рассмотрим ,,.

Пусть наша функция задана на некотором . Его можно представить как прямое произведение,,.

Теорема.Предположим- интегрируема наи.интегрируема на, то есть, тогдаинтегрируема понаи.

Интеграл слева – повторный интеграл, справа – кратный.

Доказательство.

В

ведем разбиениена, по следствию к основной теореме мы можем разбить просто на квадратики, тогда рассмотрим интегральные суммы.

Введем разбиение на.

.

У нас получилось разбиение всего на.

, умножим все наи просуммируем.

Следствие.Пусть- интегрируема на- ограниченном множестве, тогда рассмотриммножество- сечение плоскостью.

Если интегрируема понаи,интегрируема пои, где.

Мы доказали теорему в случае, когда область прямоугольная. Докажем теперь справедливость равенства для произвольной области.

Доказательство.

ограниченное, принадлежащее.,интегрируема на.

содержится в некотором. Чтобы применить на нем теорему, доопределим- по аддитивным свойствам она интегрируема.

Доказано.

Пример 1. Сведение двойного интеграла к повторному.

Область- непрерывные.

- интегрируема на. Сведем к повторному:

,

.

Пример 2. Тройной интеграл.

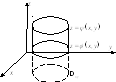
- измеримое.

- непрерывны на.

Если интегрируема, то

Пример 3.- ограниченная,.