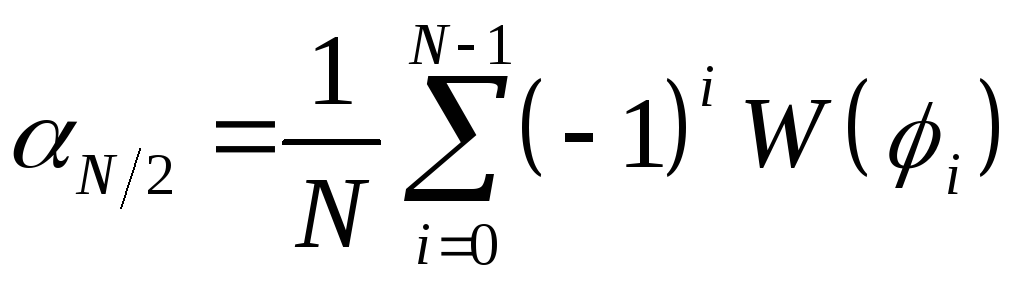- •Автоматизация оптических измерений
- •2013, С неопубл. Испр. 2017
- •Ббк сгау 34.9
- •Сведения об авторе
- •Содержание
- •Определения, обозначения и сокращения
- •Предисловие
- •Введение
- •Двумерный лазерный триангулятор
- •1.1 Сбор данных
- •1.2 Обработка данных
- •1.3 Программное обеспечение
- •1.3.1 Программа сбора данных
- •1.3.2 Программа обработки данных
- •1.3.3 Программа статистической обработки результатов измерений
- •1.3.4 Результаты работы программы статистической обработки измерений
- •1.4 Требования к качеству контролируемой детали по отклонениям геометрической формы поверхности вращения
- •1.5 Требование к погрешности измерительного канала автоматизированной системы
- •1.5.1 Требования к производственному контролю
- •1.5.2 Требования к погрешности измерений
- •1.7 Сравнительный анализ кругломеров различного типа
- •2 Характеристики измерительного канала двумерного лазерного триангулятора
- •2.1 Проектирование источника излучения
- •2.2 Влияние шумов на характеристики измерительного канала
- •2.3 Возможные пути увеличения чувствительности и уменьшения погрешности автоматизированной системы
- •2.4 Оценка влияния шумов измерительного канала
- •3 Измерения геометрических величин двумерным лазерным триангулятором при больших отклонениях от круглости
- •4 Пример информационного расчета автоматизированной системы
- •5 Комплекс технических средств
- •5.1 Современное состояние
- •5.2 Перспективы
- •Заключение
- •Список использованных источников
- •Приложение а Обработка данных в двумерном лазерном триангуляторе
- •Приложение б Преобразование пучка света в оптической системе в приближении геометрической оптики
- •Приложение в Описание сфокусированного пучка света лазера
- •Приложение г Листинг программы численного расчета изменения величин информативных параметров двумерного лазерного триангулятора под влиянием электронных шумов
- •Приложение д Обработка данных в двумерном лазерном триангуляторе при больших отклонениях от круглости
- •Приложение е Примеры приложений к техническому заданию на дипломное проектирование
- •Назначение системы
- •2 Характеристики объекта автоматизации
- •Требования к информационному обеспечению
- •2 Характеристика объекта автоматизации
- •3 Требования к информационному обеспечению:
- •4 Требования к техническому обеспечению:
- •5 Требования к программному обеспечению:
- •6 Общие требования к ас:
- •7 Требования к методическому обеспечению
- •8 Технические требования к ас:
- •1 Назначение системы:
- •4 Условия работы системы
- •5 Требования к техническим характеристикам системы
- •6 Общие требования к проектируемой системе
- •Приложение ж
- •Приложение и Листинг программы обработки данных «2009Mmod»
- •Приложение к Файл данных от детали с гранностью
- •Заякин Олег Александрович автоматизация оптических измерений
- •443086 Самара, Московское шоссе, 34.
- •443086 Самара, Московское шоссе, 34.
Приложение а Обработка данных в двумерном лазерном триангуляторе
Формулы для обработки данных рассматриваемой АС подробно описаны в [5]. Для численного восстановления контролируемые поверхности представим формулой следующего вида:
|
|
|
(А.1) |
где
![]() ,
,![]() ,
,![]() ‑
цилиндрические координаты,
‑
цилиндрические координаты,![]() ‑
функция номинального профиля,
‑
функция номинального профиля,![]() ‑
функция отклонения от номинальной
формы. Величины
‑
функция отклонения от номинальной
формы. Величины![]() и
и![]() отсчитываются в направлении
отсчитываются в направлении![]() .
.![]() Система
координат
Система
координат![]()
![]() ,
,![]() ,
,![]()
![]() ,
жестко связана с контролируемой
поверхностью.
,
жестко связана с контролируемой
поверхностью.
Вычисление искомых координат контролируемой поверхности производится из формул для определения координат освещенной точки контролируемой поверхности на каждом шаге сканирования. Они выражают собой законы геометрической оптики для отражения света: первый ‑ прямолинейность распространения световых лучей, второй ‑ равенство угла падения углу отражения и третий ‑ то, что падающий луч, отраженный луч и нормаль к поверхности в точке падения луча лежат в одной плоскости:
|
|
|
(А.2) |
где, только в пределах этих двух формул, квадратными скобками обозначено векторное произведение, круглыми скобками – скалярное произведение; в знаменателе обозначен модуль векторов, то есть, их длина.
Из системы уравнений (А.2) получаем дифференциальное уравнение:
|
|
|
(А.3) |
где ![]() является функцией переменных:
является функцией переменных:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]() ‑
смещение источника излучения в направлении
осиOZ;
‑
смещение источника излучения в направлении
осиOZ;
![]() ‑
поворот контролируемой детали вокруг
осиOZ.
‑
поворот контролируемой детали вокруг
осиOZ.
Функция в правой части уравнения имеет вид:
|
|
|
(А.4) |
где
|
|
|
(А.5) |
![]() ,
,![]() и
и![]() ‑
координаты освещенной точки контролируемой
поверхности в цилиндрической системе
координат, жестко связанной
с оптико-механическим блоком (XYZна рисунке 2).
‑
координаты освещенной точки контролируемой
поверхности в цилиндрической системе
координат, жестко связанной
с оптико-механическим блоком (XYZна рисунке 2).
При этом уравнения связи между двумя названными системами координат имеют вид:
|
|
|
(А.6) |
Отметим,
что
![]() .
Величины
.
Величины![]() и
и![]() ,
а также тесно связанная с последней
,
а также тесно связанная с последней![]() ‑
это измеряемые параметры. Они ‑
функции переменных
‑
это измеряемые параметры. Они ‑
функции переменных![]() и
и![]() ,
задаваемые дискретными отсчетами в
процессе сканирования, а также неизвестной
переменной
,
задаваемые дискретными отсчетами в
процессе сканирования, а также неизвестной
переменной![]() .
Величины
.
Величины![]() и
и![]() назовем «параметрами настройки» [18],
они задаются оператором вручную и в
цикле измерения остаются постоянными.
назовем «параметрами настройки» [18],
они задаются оператором вручную и в
цикле измерения остаются постоянными.
Функция
вида
![]() является частным решением уравнения
(А.3) при каком-нибудь постоянномz и
при граничном условии
является частным решением уравнения
(А.3) при каком-нибудь постоянномz и
при граничном условии
|
|
|
(А.7) |
где
![]() обозначает конкретный радиальный
профиль, на котором рассматриваются
эти условия. Из сетки таких профилей
можно получить изображение всей
контролируемой поверхности. Важно
отметить, что при получении радиального
профиля используются данные, собранные
только с него самого.
обозначает конкретный радиальный
профиль, на котором рассматриваются
эти условия. Из сетки таких профилей
можно получить изображение всей
контролируемой поверхности. Важно
отметить, что при получении радиального
профиля используются данные, собранные
только с него самого.
Граничное
условие (А.7), при малых отклонениях
![]() от своей средней величины вдоль
восстанавливаемого профиля поверхности,
позволяет получить аналитическое
решение при замене нелинейного
дифференциального уравнения (А.3)
упрощенным дифференциальным уравнением,
полученным путем его линеаризации в
окрестности средних интегральных, по
этому профилю, величин
от своей средней величины вдоль
восстанавливаемого профиля поверхности,
позволяет получить аналитическое
решение при замене нелинейного
дифференциального уравнения (А.3)
упрощенным дифференциальным уравнением,
полученным путем его линеаризации в
окрестности средних интегральных, по
этому профилю, величин![]() ,
,![]() и
и![]() .
.
Из (А.3) получаем дифференциальное уравнение следующего вида:
|
|
(А.8) |
где
 ,
,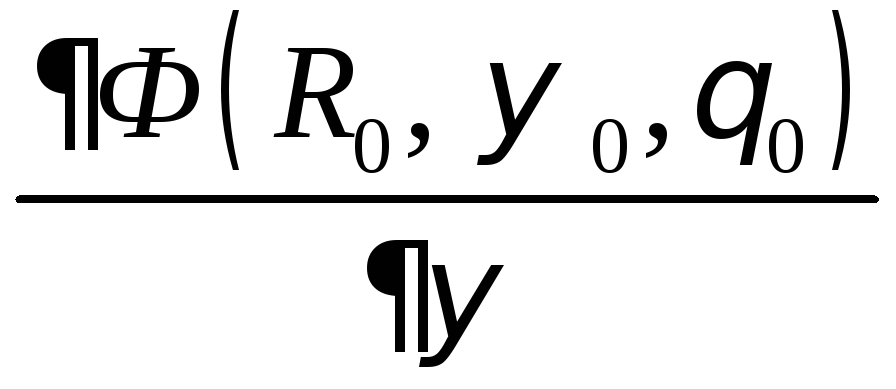 и
и
![]() означают частные производные функции
означают частные производные функции![]() ,
взятые при
,
взятые при![]() ,
,![]() и
и![]() ;
;
![]() ,
,![]() и
и![]() ‑
средние интегральные величины
‑
средние интегральные величины![]() ,
,![]() и
и![]() по радиальному профилю. Точнее, в рамках
используемой модели, это величины,
которые бы имели место при идеальной
круглости контролируемой детали. В
расчетах мы их заменяем на средние
интегральные величины. Они должны быть
рассчитаны по тому радиальному профилю,
по которому решается (А.8).
по радиальному профилю. Точнее, в рамках
используемой модели, это величины,
которые бы имели место при идеальной
круглости контролируемой детали. В
расчетах мы их заменяем на средние
интегральные величины. Они должны быть
рассчитаны по тому радиальному профилю,
по которому решается (А.8).
Считаем,
что в (А.8) приращения переменных
![]() ,
,![]() и
и![]() независимы, а также, что зависимостью
независимы, а также, что зависимостью![]() от других переменных можно пренебречь.
Приращение
от других переменных можно пренебречь.
Приращение![]() равно нулю для заданного радиального
профиля. Поэтому производные в ряде
Тейлора в (А.8) записаны как частные, а
два последних слагаемых отсутствуют.
равно нулю для заданного радиального
профиля. Поэтому производные в ряде
Тейлора в (А.8) записаны как частные, а
два последних слагаемых отсутствуют.
Еще
одно упрощение, сделанное при переходе
от (А.3) к (А.8) – это замена сомножителя
![]() в правой части (А.3) на
в правой части (А.3) на![]() .
Для заданного радиального профиля, по
которому решается (А.8), это величина
постоянная. Она записана в левой
части (А.8) для удобства дальнейших
преобразований этого уравнения.
.
Для заданного радиального профиля, по
которому решается (А.8), это величина
постоянная. Она записана в левой
части (А.8) для удобства дальнейших
преобразований этого уравнения.
Подставим
в уравнение (А.3) вместо
![]() и
и![]() значения
значения![]() и
и![]() и приравняем нулю его правую часть.
Тогда для нахождения
и приравняем нулю его правую часть.
Тогда для нахождения![]() ,
нужного нам для дальнейших расчетов,
получим уравнение:
,
нужного нам для дальнейших расчетов,
получим уравнение:
|
|
|
(А.9) |
Это уравнение имеет аналитическое решение, однако оно довольно громоздко, и в программе оно решается численно.
Запишем (А.8) в виде:
|
|
|
(А.10) |
где
|
|
|
|
|
|
|
|
Уравнение (А.10) решается при граничном условии
|
|
|
(А.11) |
где
![]() обозначает конкретный радиальный
профиль.
обозначает конкретный радиальный
профиль.
Для
каждого
![]() имеется свое уравнение (А.10), отличающееся
только значениями коэффициентов
имеется свое уравнение (А.10), отличающееся
только значениями коэффициентов![]() ,
,![]() ,
,![]() .
.
С целью аппроксимации, либо фильтрации измерительной информации функцию
|
|
|
(А.12) |
удобно представить в виде разложения в ряд Фурье. В этом случае решение дифференциального уравнения (А.10) можно получить в общей форме через соответствующие коэффициенты разложения. Для данных в цифровой форме при этом наиболее подходит дискретное преобразование Фурье [7]. Напишем, как выглядит решение уравнения (А.10), полученное с помощью этого преобразования. В пределах обсуждения этого преобразования индексы при переменных показывают номер гармоники спектра, или порядковый номер отсчета точек профиля.
Пусть
функция
![]() задана своими дискретными отсчетами
задана своими дискретными отсчетами![]() с равномерным шагом по радиальному
профилю;
с равномерным шагом по радиальному
профилю;![]() ;
;![]() ;
;![]() .
Тогда она однозначно представима в виде
конечного ряда Фурье в виде:
.
Тогда она однозначно представима в виде
конечного ряда Фурье в виде:
|
|
|
(А.13) |
где
![]() ,
,![]() ‑
целая часть. Коэффициенты этого ряда
Фурье вычисляются по формулам:
‑
целая часть. Коэффициенты этого ряда
Фурье вычисляются по формулам:
|
|
(А.14) |
где
![]() .
.
Тогда искомый радиальный
профиль представлен дискретными
отсчетами высоты
![]() в
в![]() точках при тех же значениях
точках при тех же значениях![]() ,
что и
,
что и![]() :
:
|
|
(А.15) |
где
![]() .
.
Таким образом, найдена алгебраическая связь между параметрами гармоники Фурье-спектра функций (А.12) и соответствующей гармоники (то есть, с тем же числом волн на оборот поверхности) Фурье-спектра профиля высот контролируемой поверхности.
Выражения (А.4) – (А.6), (А.9), (А.10), (А.12) – (А.15) представляют собой функцию преобразования автоматизированной системы.

 ,
, ,
, ,
, ,
, ,
,
 ,
,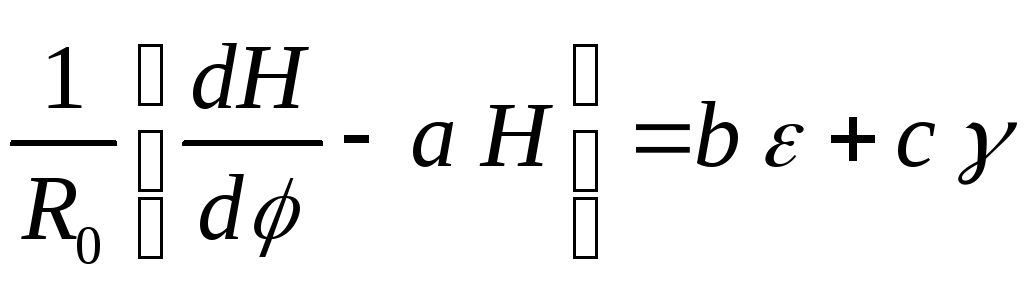 ,
,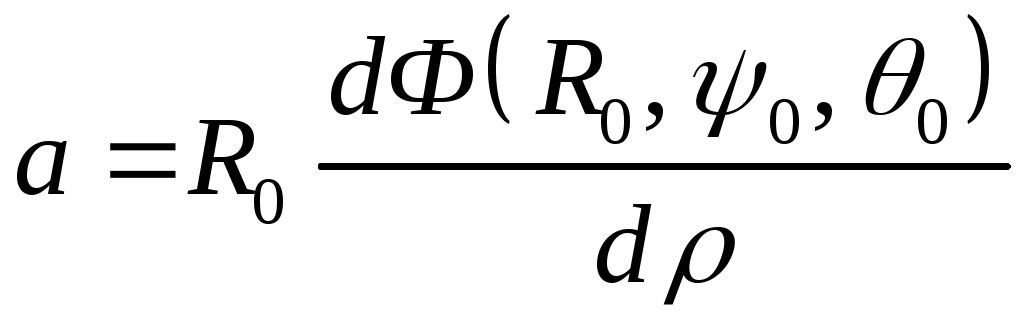 ,
, ,
, ,
, ,
, ,
, ,
,