ALL

ТРЕХМЕРНЫЕ СДВИГИ

•Недиагональные элементы в верхней левой 3 х 3-подматрице обобщенной матрицы преобразования размером 4x4 задают сдвиги в трех измерениях, т. е.

			1	b	c	0
	X T x y z	1 d 1 f				0	x dy gz	bx y iz			cx fy z	s
		g		i	1	0
			0	0	0
						s					0,85 0,25		0
	Пример - Применим преобразование сдвигов									1
								T		0,75	1	0,7	0
	к единичному кубу
										0,5	1	1
													0
	•									0	0	0	1

• получим сдвиг куба без масштабирования																	A *
													0,5	1	1	1
		0	0	1	1
																1 B *
													1,5	0,15	1,25				y*
		1	0	1
					1			0,85								C *
	1		1	1	1		1		0,25	0			0,75	0,25	1,95
X * X T																1				C*
												0,25
	0		1	1	1	0,75		1	0,7	0				2	1,7	1 D *
	0		0	0	1		0,5	1	1				0	0	0	E *			D* B*	G*
		1	0	0						0						1
					1		0	0	0	1			1	0,85	0,25	1 F *
	1		1	0	1								0,25	0,15	0,95				A*	F*
																1 G *
	0		1	0	1							0,75		1	0,7	1 H *
																				x
																			E*

z*

ПРОСТРАНСТВЕННЫЙ ПЕРЕНОС

•За переносы отвечает нижняя подматрица матрицы преобразования. Матрица пространственного переноса имеет вид:

1	0	0	0
T 0	1	0	0
0	0	1	0
l	m	n	1

•Перемещенные однородные координаты получаются с помощью

преобразования					1	0	0	0
	x/			h x
		y/	z /		y z 1 0 1		0	0
					0	0	1	0
						m	n
					l			1
	• == [(x + n)			(y + m)	(z+n) 1]

•Из этого следует, что преобразованные физические координаты равны

•х* =х + 1,

•у* =у + m,

•z* = z + n.

• Изменение масштаба

• вдоль оси ‘x’ в ‘a’-раз

a 0 0 0

0 1 0 00 0 1 00 0 0 1

•всей фигуры

a 0 0 0		1 0 0 0
0 a 0 0		0 1 0 0
		a
0 0 a 0		0 0 1 0
0 0 0 1		0 0 0 1 a

Примеры:

вдоль оси ‘y’ в ‘е’-раз		вдоль оси ‘z’ в ‘k’-раз
1 0 0 0		1 0 0 0
0 e 0 0		0 1 0 0
0 0 1 0		0 0 k 0
0 0 0 1		0 0 0 1

Параллельный перенос объекта вдоль оси

1 0 0 0		1 0 0 0		1 0 0 0
0 1 0 0		0 1 0 0		0 1 0	0
0 0 1 0		0 0 1 0		0 0 1	0
l 0 0 1		0 m 0 1		0 0	n 1

l– параллельный перенос объектов вдоль оси x, m– параллельный перенос объектов вдоль оси y, n– параллельный перенос объектов вдоль оси z,

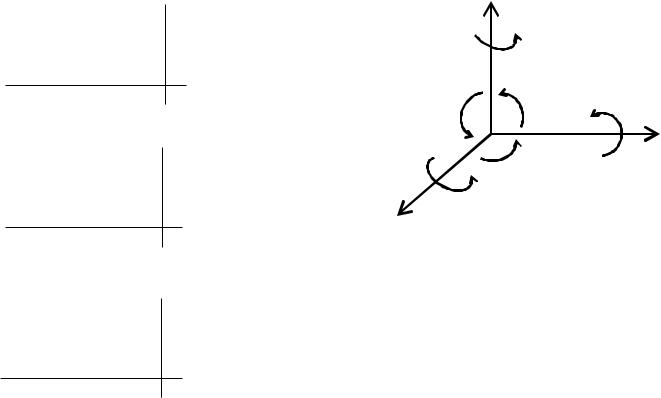
Поворот тела вокруг оси на произвольный угол:

Поворот фигуры вокруг оси ‘z’

cos		sin		0	0			y
sin		cos		0	0
Tz	0		0	1	0
	0		0	0	1
Поворот фигуры вокруг оси ‘х‘								x
1	0		0		0
0	cos		sin		0		z	α
Tx 0	sin		cos		0
	0		0
0					1
Поворот фигуры вокруг оси ‘y’
cos		0	sin		0		• Правосторонняя система
	0	1	0		0
Ty sin		0	cos		0			координат. Поворот против
	0	0	0					часовой стрелки, если смотреть
					1

из конца оси в начало координат.

При переходе от ‘z’ к ‘х’ (‘х’ к ‘у’) вся таблица смещается на один элемент вправо и вниз не выходя за границы матрицы 3х3

Композиции преобразований

•Последовательные преобразования могут быть скомбинированы или объединены в одно 4 х 4-преобразование, дающее тот же самый результат.

•Так как перемножение матриц является некоммутативной операцией, то важен порядок ее выполнения (в общем случае [А] [В] [В] [А]).

•Правильный порядок определяется положением конкретной матрицы преобразования относительно матрицы координатного вектора. Матрица, ближайшая к матрице координатного вектора, задает первое преобразование, а последняя — последнее преобразование. Математически это можно записать следующим образом:

•[Х][Т]= [Х][Т1][Т2][Т3][Т4]...,

•где

•[Т]= [Т1][Т2][Т3][Т4]...

•и [Ti] являются произвольной комбинацией матриц масштабирования, сдвига, вращения, отражения, переноса, перспективного преобразования и проецирования.

•Так как перспективные преобразования искажают геометрические объекты, а преобразования проецирования приводят к потере информации, то в случае наличия этих матриц они должны быть расположены соответственно предпоследней и последней по порядку.

ПОВОРОТ ВОКРУГ ОСИ, ПАРАЛЛЕЛЬНОЙ КООРДИНАТНОЙ

Часто необходимо вращать объект вокруг оси, не совпадающей с х, у и z. Рассмотрим частный случай для оси, параллельной одной из координатных осей х, у или z.

•На рис. 5 изображено тело в локальной системе осей x'y'z', параллельных фиксированной глобальной системе xyz. Процедура

–переместить тело так, чтобы локальная ось совпала с координатной;

–повернуть вокруг указанной оси;

–переместить преобразованное

тело в исходное положение. •

	• Математически это можно записать•
		так:	•
			•
	•	[X*] = [X][T ][R ][T ]-1
		r x r	•
	•	где

рис. 5

[X*] – преобразованное тело, [X] – исходное тело,

[Tr] – матрица перемещения,

[Rx] – соответствующая матрица поворота,

[Tr]-1 – матрица, обратная к матрице перемещения.

ПОВОРОТ ВОКРУГ ПРОИЗВОЛЬНОЙ ОСИ В ПРОСТРАНСТВЕ

•Обобщенный случай поворота вокруг произвольной оси в пространстве выполняется с помощью переноса и простых поворотов вокруг координатных осей. Так как метод поворота вокруг координатной оси известен, то основная идея заключается в том, чтобы совместить произвольную ось вращения с одной из координатных осей.

•Предположим, что произвольная ось в пространстве проходит через точку

(x0,y0,z0) с направляющим вектором (cx,cy,cz). Поворот вокруг этой оси на некоторый угол выполняется по следующему правилу:

1.выполнить перенос так, чтобы точка (x0,y0,z0) находилась в начале системы координат;

2.выполнить соответствующие повороты так, чтобы ось вращения совпала с осью z;

3.выполнить поворот на угол вокруг оси z;

4.выполнить преобразование, обратное тому, что позволило совместить ось вращения с осью x;

5.выполнить обратный перенос.

ПОВОРОТ ВОКРУГ ПРОИЗВОЛЬНОЙ ОСИ В ПРОСТРАНСТВЕ

•В общем случае для того, чтобы произвольная ось, проходящая через начало координат, совпала с одной из координатных осей, необходимо сделать два последовательных поворота вокруг двух других координатных осей.

•Для совмещения произвольной оси вращения с осью z сначала выполним поворот вокруг оси х, а затем вокруг оси у.

•Чтобы определить угол поворота вокруг оси х, используемый для перевода произвольной оси в плоскость xz, спроецируем сначала на плоскость yz направляющий единичный вектор этой оси (рис. 7 а). Компоненты у и z

спроецированного вектора равны cу- и cx-компонентам единичного направляющего вектора оси вращения. Выбор координатной оси (в данном случае z) произволен. Из рисунка определим

d cy2 cx2

cos cdx

sin cy d

рис. 7 Повороты, необходимые для совмещения с осью z единичного вектора OP. (а) Поворот вокруг x; (b) поворот вокруг у.

ПОВОРОТ ВОКРУГ ПРОИЗВОЛЬНОЙ ОСИ В ПРОСТРАНСТВЕ

•После перевода в плоскость xz с помощью поворота вокруг оси х,

•z-компонента единичного вектора равна d,

•а x-компонента равна cx, т.е. x-компоненте направляющего вектора, как это показано на рис. 7 b.

•Длина единичного вектора равна 1.

•Таким образом, угол поворота вокруг оси у, необходимый для совмещения произвольной оси с осью z, равен

•cos = d, sin = cx.

•Тогда полное преобразование можно представить в виде

•	[М] = [Т] [R	] [R ] [R ] [R ]-1			[R	] -1	[Т]-1,		1	0		0		0
	x	y		y	x
•	где матрица переноса равна						T		0	1		0		0
									0	0		1		0
•								x		y	0	z	0	1
									0

•Матрица преобразования поворота вокруг оси x

•
							1			0				0	0
									cx					cy
		1	0	0	0		0								0
R		0	cos	sin	0					d				d
	x
		0	sin	cos	0		0				cy			cx	0
		0	0	0	1
											d			d
										0				0
							0								1

ПОВОРОТ ВОКРУГ ПРОИЗВОЛЬНОЙ ОСИ В ПРОСТРАНСТВЕ

• и вокруг оси у	cos		0	sin	0		d		0	cx	0
•		0	1	0	0		0		1	0	0
	Ry sin		0	cos	0	c		x	0	d	0
•
		0	0	0			0		0	0
					1						1

•Вращение вокруг произвольной оси задается матрицей поворота вокруг оси z

•	cos		0	sin	0
Rz		sin	1	cos	0
		0	0	1	0
		0	0	0
					1

•На практике углы и не вычисляются явным образом. Элементы матриц

поворотов [Rx] и [Ry] получаются за счет выполнения двух операций деления и извлечения квадратного корня.

•Если компоненты направляющего вектора произвольной оси неизвестны, то,

зная вторую точку (xi,yi,zi) на оси, их можно определить, нормализовав вектор, соединяющий первую и вторую точки. Более точно вектор оси из (x0,y0,z0) в

(xi,yi,zi) равен [V] = [(xi - х0) (yi – y0) (zi - z0)].

•Нормализация дает компоненты направляющего вектора:

•	cx	cy	cz	xi x0		yi y0	zi z0
								1
				2		2	2
								2
				xi x0	yi y0		zi z0