§6. степенные функции с рациональными показателями

В этом параграфе рассматривается степень с дробным показателем. Ýто позволяет ввести и исследовать степенные функции с произвольными рациональными показателями, имеющие широкое применение.

1. Степень с рациональным показателем и ее свойства

						Из определения арифметического корня вытекает,
						что если m	— целое число,	п — натуральное и m
						делится на	п, то при а > 0 справедливо равенство:
			m
							(	)
	n am	= a n . Например 5 335
							= 37 , так как 37	5 = 335. С другой сторо-
	ны,	37	= 3	35			35
				5	. Итак, 5 335 = 3 5 .

m

Вполнеестественнымявляетсяжеланиеформулу a n = n am принять в качестве определения степени с рациональным показателем, то есть для произвольных целых m и натуральных п > 1.

Степенью положительного числа а с рациональным показателем mn , где m — целое число, п — натураль-

ное, большее 1, называется число n am .

Обозначение степени положительного числа а с рациональ-

					m	По определению,			m	Так,
ным показателем обычное: a n .									a n = n am .
1		= 2; 27−	2		1			1 .
83	= 3 8		3	= 3 27−2 = 3			=
					272
								9

!Условие а > 0 вызвано тем, что степени с рациональными показателями определены с помощью операции извлечения корня, которая не всегда выполняется для отрицательных чисел.

100 Функции, их свойства и графики

Степень с основанием, равным нулю, определяется лишь для

положительного дробного показателя. По определению,		m	,
		0 n = 0
2	= 00,5 = 0 .
где m, n N: 03

Степени с рациональными показателями обладают теми же свойствами, что и степени с целыми показателями.

Если р и q — рациональные числа и а — положительное число, то справедливы соотношения:

ap aq = ap+q (свойство 1); ap :aq = ap−q (свойство 2);

(ap )q = apq (свойство 3).

Если р — рациональное число, а и b — положительные числа, то справедливы соотношения:

(ab)p = ap bp (свойство 4);

a p		ap		(свойство 5).
	=	b	p
b

Из свойства 1 вытекает, что для а > 0 и p Q выполняется равенство:

a−p = a1p .

Действительно, ap a−p = ap+(−p) = a0 =1.

Из свойства 3 вытекает, что для а > 0, p Q, n N, n > 1 выполняется равенство:

p

nap = an .

Спомощью указанных свойств преобразовывают выражения, содержащие степени с рациональными показателями, и вычисляют их значения.

		3	4	3		4	1		= (34 )−	1		1	1		1
	Например,	814	:815	= 814	−	5 =	81−				= 3−	5 =		=		.
								20		20
													1
													35	5 3
Пример 1.		Вычислить:
						1	1
1)	4 250 54 :2−	4 ;								3) 1+ 20,5				2 −21,5 .
				2) 123			63 ;
	1	3								(			)
						1
						93
	 1) Воспользуемся определением степени с дробным показа-
телем и свойствами (1) и (2):

Степенные функции с рациональными показателями

101

1			3	1		−3			2	1	5	3	5	1	1			3	3	+1
		−								4		4		4		−
	:2				:2										= 24		−
4 250 54			4 = 4 2	53 54		4		=				3						4	54	4 = 21 51 =10.
											2−4
2) Согласно свойствам 4 и 5 степени с дробным показателем,
имеем:				1	1
							12 6					1
				123	63							3			1
				1		=			9				= 8		3 = 2.
				93
3)Воспользовавшисьформулойквадратасуммыдвухвыражений
и свойствами 1 и 3 степени с дробным показателем, получим:
(	)						(		)
1+ 20,5 2 − 21,5 =				1+ 2 20,5		+		20,5		2 −		21,5 =1+ 21+0,5 + 22 0,5 − 21,5 =

=1+ 21,5 + 2− 21,5 = 3.

Ответ. 1) 10; 2) 2; 3) 3.

Вычисление степеней с рациональными показателями удобно выполнять с помощью калькулятора.

Пример 2. Население города насчитывает 225 тысяч человек и растет ежегодно на 3% в сравнении с

предыдущим годом. Каким станет население города через 5 лет?

Население города ежегодно увеличивается в 1,03 раза, и через год оно будет насчитывать 225·1,03 тысяч человек. За следующий год оно опять увеличится в 1,03 раза и составит 225 · 1,03 · 1,03 = = 225 · (1,03)2 тысяч человек. Рассуждая аналогично, получим, что население города через 5 лет увеличится до 225·(1,03)5 ≈ 261 тысячи человек. Для вычислений мы воспользовались калькулятором.

Ответ. ≈ 261 тыс.

Пример 3. Скорость проникновения воды в почву вычисляется по экспериментально установленной формуле:

v15 5t−1 ,

=+ 2

где v	— скорость проникновения воды в почву, мм/ч; t — время, ч.
Найдите значение v при t = 0,1; 0,2; 0,5; 1,0; 2,0; 5,0.
	Для вычислений можно воспользоваться калькулятором. В
результате получим:
	t	0,1	0,2	0,5	1,0	2,0	5,0
	v	30,8	26,2	22,1	20,0	18,5	17,3	

102	Функции, их свойства и графики

9 Контрольне вопросы

1.Как представить степень с дробным показателем в виде корня:

3	;	7	3	;	4−	2	;	30,5; 10−0,2; б)	2	;	b−	5	;	c0,8 ;	d−1,4;	m1	2	?
а) 54			2			3			a3			2					5

2.Как записать в виде степени с рациональным показателем выражение:

а) 4 73 ;	б) 6 32 ;	в)	3 0,1 ;	г)	7 a3 ,a ≥ 0 ; д) 4 a−3 ?
3°. Какие из выражений не имеют смысла:						1
а) 03;	б) 30;	в)	(−3)0 ;	г)				д) 4 a−3 ?
					(	−3)5	;

4°. Как представить в виде степени выражение:

1 1

2

3

2

3

1 1

а)

;

б)

;

в)

−

5

;

г)

?

a6 a3

a3

: a4

a

3

a3 b3

5.При каких значениях х имеет смысл выражение:

а) 3 x;	б) x;	в)	1	;	г)	x−	1	;	д) x−3 ;	е) 4 x−3 ?
			x3				3

1

6. Как вычислить значение 1574 на калькуляторе, выполняющем только четыре арифметических действия и извлечение

квадратного корня?

2. Свойства и графики степенных функций с

рациональными показателями

Свойства и графики степенных функций у = хα, где α — некоторое рациональное число, зависят от зна- чений показателя степени α. В § 5 рассматривались свойства и графики степенных функций с натуральными показателями. Рассмотрим теперь степенные функции с целыми отрицательными показателями, то есть функции вида у = х–1, у = х–2, у = х –3, у = х –4 и т. д. Сначала исследуем функции с нечётными отрицательными показателями у = х–1, у = х–3, у = х–5, … .

Функция у = х–1 или y = 1x уже рассматривалась ранее (см. § 3).

Она определена для всех х, кроме 0, является нечётной, убывает на каждомизпромежутков(–∞;0)и(0;+∞).Еёграфикомявляетсягипер- бола (рис. 67). Функции у = х–3, у = х–5, … имеют аналогичные свойс-

тва, их графики имеют вид, подобный графику функции y = 1x .

Степенные функции с рациональными показателями

103

Теперь рассмотрим степенные функции с чётными отрицательнымипоказателями,тоестьфункциивидау= х–2,у= х–4 ....Функция

у = х–2, или	1					определена для всех х, кроме 0. Она чётна, так
	y =
		x2
как y(−x) =	1			=			1	= y(x). Функция принимает положитель-
	(−x)2						x2

ные значения, то есть ее график лежит в верхней полуплоскости. График функции не пересекает ось ординат, так как при х = 0 функция не определена. Если аргумент принимает положительные значения и растет, то знаменатель дроби

x12 увеличивается, а сама дробь уменьшает-

ся. Следовательно, функция у = х-2 убывает на промежутке (0; +∞). Поскольку эта функция чётна, то она возрастает на промежутке (–∞; 0). Ее график изображен на рис. 96. Фун-

кции у = х–4, у = х–6 , … обладают подобными свойствами и имеют похожие графики.

Пример 4. Дана функция f(x) = (x − 2)−2 .

1)	Указать ее область определения.
2)	Построить ее график.			1
3)	Проходит ли график этой функции через точку		5;			?
		A		9

4)Найти точки пересечения графика функции с осями координат.

5)Сколько корней имеет уравнение f(x) = 7?

	 1) Функция y = (x − 2)−2 =	1	определена при всех дейс-
		(x − 2)2

твительных значениях х, кроме х = 2, то есть ее областью определения является

множество (−∞;2) (2;+∞).

2) График функции можно получить из графика функции y = x12 параллель-

ным переносом последнего на 2 единицы в положительном направлении оси абсцисс (рис. 97).

	104			Функции, их свойства и графики
	3) Чтобы проверить, проходит ли график функции через точку
		1		, найдём значение функции в точке х = 5: f(5) = (5	− 2)	−2	=
	A 5;	9
	= 3−2	=	1	. Следовательно, график функции проходит через точку А.
			9		1
	4) Ось абсцисс график не пересекает, поскольку дробь
					(x − 2)2

не равна нулю ни при одном значении х. Чтобы найти точку пере-

сечения графика с осью

у, найдем значение функции при х = 0:

f(0) = (0 − 2)−2

= (−2)−2 =

1

. Следовательно, график функции пере-

секает ось у

в точке

4

координатами

с

0;

1

4

.

6) Для ответа на вопрос нужно выяс-

нить, в скольких точках функция при-

нимает значение 7. Прямая у = 7 пере-

секает график функции в двух точках

(рис. 98). Следовательно, в двух точках

функция принимает значение 7. Урав-

нение имеет два корня.

Выше уже отмечалось, что с помощью степенных функций описываются различные процессы и явления. В некоторых случаях показатель степени не является целым числом. Например, период Т коле-

бания математического маятника пропорционален длине маят-

	1		l		1
ника l в степени					2
	2	, а именно: T = 2π				, где g – ускорение сво-
		g

бодного падения. Если газ расширяется или сжимается без теплообмена с окружающей средой, то его давление Р и объем V

связаны формулой: V = PCα , где С — некоторая постоянная. В

частности, для воздуха эта формула приобретает вид: V = PC−1,4 .

Поэтому полезно знать свойства степенных функций y = xα , когда показатель степени α не является целым числом.

Степенные функции с рациональными показателями

105

!В зависимости от свойств функции выделяют три слу-

чая: 0 < α < 1, α > 1 и α < 0.

Пусть 0 < α < 1. В частности, это может быть и функция	1
	у = x2 .
1
По определению степени, x2 = x . Свойства и график функции
1	и x
y = x рассматривались ранее. Поскольку выражения x2

определены при одних и тех же значениях х, а именно при х ≥ 0,
и принимают при одинаковых значениях	х одинаковые значения,
1	и y = x	равны. Поэто-
то можно утверждать, что функции у = x2
1		что и функция
му функция у = x2 обладает теми же свойствами,

y = x , а именно, она:

1) определена на промежутке [0; + ∞);

2) принимает любые неотрицательные значения;

3) имеет единственный нуль х = 0;

4) возрастает;

5) непрерывна.

Ее график проходит через точки с координатами (0; 0) и (1; 1) и представлен на

рис. 99. Функции y = xα с произвольным

показателем 0 < α < 1 имеют аналогичные свойства и похожий график.

Пусть α > 1 и α не является целым чис- лом. Рассмотрим, например, функцию

3

y = x2 . Согласно определению степени, она

задана на промежутке [0; + ∞). Рассматривая таблицу значений функции, можно заметить, что большему значению аргумента соответствует большее значение функции. Можно предположить, что функция возрастает. Это в действительности так, хотя доказательство мы не приводим в связи с его сложностью.

	х	0	1	1	1	4	9
			9	4
	у	0	1	1	1	8	27
			27	8

График функции проходит через точки с координатами (0; 0) и (1; 1) и показан на рис. 100. Такие же свойства и подобный график

106 Функции, их свойства и графики

имеют все степенные функции с нецелым показате-

лем, большим 1. И, наконец, типичный

график степенной функции с отрицательным нецелым показателем изображен на

рис. 101. Опишите по гра- фику основные свойства

этих функций.

Пример 5. Дана функция у = (х – 2)1,4.

1)Указать ее область определения.

2)Построить ее график.

3)Определить количество корней уравнения (х – 2)1,4 = х–0,4.

1) Область определения функции находится из неравенства

х– 2 ≥ 0, то есть D(y) = [2; +∞).

2)График данной функции можно получить параллельным

переносом графика функции y = x1,4 на 2 единицы в положительном направлении оси х (рис. 102).

3)Построим на одном рисунке графики функций у = (х – 2)1,4 и у = х-0,4 (рис. 103). Графики имеет одну общую точку, то есть уравнение имеет один корень.

Пример 6. Зависимость максимальной интенсивности осадков от их длительности в некоторой местности описывается формулой:

I =13,1 t−0,56 ,

где I — максимальная интенсивность осадков, мм/ч; t — длительность осадков, ч. Найти:

1) максимальную интенсивность осадков при их длительности:

0,5 ч; 1 ч; 2 ч;

Степенные функции с рациональными показателями

107

2)при какой длительности осадков максимальная интенсивность будет равняться 3,6 мм/ч;

3)при какой длительности осадков максимальная интенсивность выше: при t1 = 32 ч или при t2 = 43 ч.

 1) I(0,5) =13,1 0,5−0,56 ≈19,3; I(1) =13,1 1−0,56 =13,1;

I(2) =13,1 2−0,56 ≈ 8,89.

2) Запишем уравнение, которое необходимо решить для ответа на вопрос: 13,1t –0,56 = 3,6. Найдем значение выражения, стоящего

	в левой части и содержащего неизвестную величину:								13,1		= 3,6;
									t0,56
						25
	t0,56	=	13,1	14	14	14	14 25	= t, обе час-
				≈ 3,64; t25 ≈ 3,64. Поскольку t25			= t25 14
			3,6
						25		25
	типоследнегоравенствавозведёмвстепень					14	: t ≈ (3,64)14 ≈10,0.
	Следовательно,длительностьосадковсоставляетпримерно10часов.
								2			3
	3) Так как функция у = хр				убывающая при р < 0 и 3 <						4 , то
	2			3
	I		> I	.
	3			4	2) ≈ 10 ч; 3) при t = 2
	Ответ. 1) ≈19,3;13,1; ≈ 8,89;							ч интенсив-
	ность более высокая.						3

9 Контрольные вопросы

1°. Какие из приведенных функций не определены при х = 0 и являются чётными:

а) y = x−3 ; б) y = x2; в) y = x−2; г) y = x; д) y = x ?

2°. Какие из приведенных функций возрастают на промежутке

(0; +∞):

а)	y = x−5; б) y = x−4;	в) y = x3 ; г) y = x2; д) y = −	1	?
3°. На каком из рис. 104, а)–г) изображен график функции:			x
а)	y = (x +1)−3 ;	б) y = x−6 +1?

108

Функции, их свойства и графики

4.На рис. 105 изображены графики функ-

ций f(x) = x2,1 и g(x) = x−2,1. Сколько корней имеет уравнение f(x) = g(x)?

5°. Какое из чисел больше:
а) (– 15)-4 или (– 12)-4;
	5	−3		6		−3
б)	6		или			;
				5
	5	3	6		3	?
в)	6		или
			5

6. Пересекает ли график функции	3	прямая:
	y = x4
а) у = 0; б) у = 1; в) у = –1; г) х = 0;		д) х = 1; е) х = –1?

7.Пересекает ли график функции y = x−32 прямая:

а) у = 0; б) у = 1; в) у = –1; г) х = 0; д) х = 1; е) х = –1?

8. Какие из следующих значений может принимать функция

3

y = x5 : 0; 100; –2?

9.Какое из чисел больше:

7		2,5	7		2,5			2 −2,5			3 −2,5
а)	8		или	9		;	б)	5		или	5		;

	в) (0,292)−0,5 или (0,293)−0,5 ?
10.	Является ли функция у = хр возрастающей или убывающей,
	если: а) р = 1,6; б) р = 0,9;		в) р = 0,7?
11.	Сколько решений имеет уравнение:
	5	3	2	7
	а) x3 = x−	4 ;	б) x3 = x−	5 ?
12.	Каково множество значений функции:					7
	5	3	2	г)	y = x−		?
	а) y = x3 ;	б) y = x−4 ;	в) y = x3 ;			5

Степенные функции с рациональными показателями

109

Задачи

103°. Вычислите без использования вычислительных средств:

	1)					3	;														3	;										3) 160,25 0,125−3 ;
		814																	2) 325
	4) 5			−	3		:5−0,25 ;														−1				1	2
					4														5) 2			2	−22			.
104.	Представьте в виде степени:																																1
							2		3																				−11			−
	1°)								4		;					2°)		y−0,2 :		y0,4;					3°)								4		;								15
		a3																									x			3						4°) (5 a3 ) ;
																							5
						− 3			5				7					5			2												(6 b5			)				1
	5)							9							;	6)				−			8		7)							0					−3
		b				4					b12							a6	: a		3			;			(11 b6 )											b2 .
105.	Упростите выражение:
						1				−1					3
			a2				a					2 − a2																	3			3
	1°)																;								2°)																1;
																											x2			−1					x2	+1				+
									1 − a
	3°)				4a				−b					;											4)		1		−2					−1 2				2		−1			;
																											a3b			3		a			3b3	+ a3b					3
					1				1
			2a2						−b2																									3
	5)			a −b								;													6)			−3			−0.4					2			0,2		.
																											c	7 y						c7 y
				1					1
		a3 −b3
106. Вычислите с помощью калькулятора:
	1) 30,082 ;										2)							3	;	3) 0,671,83 ;									4)						1				5)			3 8,345 .
																21,97																15,75 ;
107.																																2			через точку с коор-
	Проходит ли график функции f(x) = x3
	динатами:																								3) (2				2; 2);							4) (2; 2							2)?
	1) (8; 4);															2) (4; 8);

108.Найдите точки пересечения графика функции у = f(x) с осями координат, если:

1°) у = (х + 2)–1;			2°) у = х–5 – 1;			3)	4	;
							f(x) = (x −1)3
4) f(x) = (x + 2)	4	;	5) f(x) = (x +1)−	4	;	6)	f(x) = (x −2)−	4
	3			3				3 .

110 Функции, их свойства и графики

109. Найдите область определения функции:

1°) у = (х – 3)5;			2°) у = (х – 3)–5;				3)	y = (x	1
									+3)5 ;
1	;		5)			1	6)	y = (5	7
4) y = (x +3)−5				y = (3 − x)−4 ;					− x)5 .
110. Дана функция			1
			y = x3 .					= 27, x2 = (0,5)−3 .
1) Найдите значение функции в точках x1
								8	A(16;23 2);
2) Проходит ли график функции через точку
(	)	; точку		(	)	?
точку B 5−3 ;5				C 5−3 ;5−1

3)Принимает ли функция значения 2; –2; 0?

4)Постройтеграфикфункцииипонемуопишитеееосновные свойства. Укажите область определения и множество значений. Является ли функция монотонной, чётной, нечётной, непрерывной?

5)Сколькокорнейимеетуравнениеx1/3 =–1;x1/3 = 3; x1/3 =2–x?

6)Сравните числа 3 0,5 и 3 43 .

7)Укажите наибольшее значение функции на промежутке

[8; 27].

111.Постройте схематически график функции:

1°)у=(х+1)–2; 2°) у = х–3 + 1; 3°)у=2х–1 +2; 4) у = х–4 – 2;

5°)			3	;		6°)		3	;	7°)	y = x0,1 ;							8) y = (x			5	;
		y = x2					y = x−2														+1)3
9)			3	−2;						2	;				11)		y = x−		7	+1.
	y = x−4							10) y = (x −2)3											5
112. Расположите по возрастанию числа:													1				1
		1 0,6		1	0,6	2	0,6				3	−			7
1)													7	,		−7		,1.
			,			,		;		2)	7
		3		5		5									3
113. Сколько корней имеет уравнение:																		1	5
1)	x2 +1 = x−0,2;							2) x3		1	;				3*)					= 2x +3		?
									= (x +1)2								x6 x−		6

1

114. Найдите степенную функцию y = ax5 , если ее график проходит через точку А(32; 1). На одном рисунке изобразите

1

график найденной функции и график функции y = x5 .

Степенные функции с рациональными показателями

111

115.Дана функция y = 3 x.

1)Укажите ее область определения.

2)Исследуйте ее на четность и нечётность.

1

3) Постройте ее график, используя график функции y = x3 . 116. Скорость резания и прочность резца связаны зависимостью:

v = T3500,2 , где v — скорость резания, м/мин; Т — прочность

резца (время между двумя переточками), мин. 1) Найдите скорость резания при Т = 40 мин.

2) Какова прочность резца при скорости резания 400 м/мин? 3*)Найдитезависимостьпрочностирезцаотскоростирезания. 4*) Существует ли оптимальная скорость резания, то есть скорость, для которой прочность резца наибольшая?

117. Объем куба равен V. Пользуясь степенью с дробным показателем, выразите через объем V:

1) длину ребра куба;

2*) площадь S грани куба;

3*) площадь поверхности Р куба.

Итог

Основное понятие

Геометричес- Определение кая интерпреПрименение

тация, примеры

Степенью положительно-

1

= 3 8

= 2;

Обобщение

поня-

го числа а с рациональ-

83

тия степени

дает

ным показателем

m

−3

3

−2

возможность

рас-

n , где

ширить запас фун-

27

2

=

27 =

m — целое число, п — на-

кций для модели-

туральное, большее 1, на-

1

= 1 .

рования реальных

зывается число

n

a

m

.

= 3

процессов.

2

27

9

Основные утверждения

ap aq = ap+q , а > 0.

ap : aq = ap−q , а > 0.

(ap )q = apq , а > 0.

(ab)p = ap bp .

a p

=

ap

, а > 0, b > 0.

b

p

b

	1		готовимся к тематичес-
			кому оцениванию по
			теме «Функции, их свойс-
			тва и графики»
?	Задания для самоконтроля
1°.	Известно, что кривая проходит через точки А(1; 0) и В(1; 1).
	Может ли эта кривая быть графиком некоторой функции?
2.	Проходит ли график функции y = x			через точку с координа-
	тами (4; –2)?
3°.	Укажите точки пересечения графика функции y = x −1 с
	осями координат.			3x + 2
4.	Какова область определения функции:
	а°) y = x + 2	;	б°) y = x + 2 ;	в) y = x −1 + 2− x ?
5°.	x2 +1		x2 −1
	Какая из следующих функций является чётной (нечётной):
	а) у = х2 + х;	б)	у = х2 – 1; в) у = х3 + 1; г) у = х3 + х?
6.	На рис. 106 изображен график функции
	y = f(x).
	а°) Какова её область определения?
	б°) Является ли функция чётной; нечёт-
	ной?
	в°) Сколько нулей имеет функция?
	г°) При каких значениях х функция при-
	нимает положительные (отрицательные)
	значения?
	д) Чему равняется сумма длин всех промежутков убывания
	функции?
	е°) Каково множество значений функции?
	ё°) Чему равно наибольшее (наименьшее) значение функции?
	ж) Сколько корней имеет уравнение f(x)= 1?
	з*) Укажите все значения а, при которых уравнение f(x)= а
	имеет два корня?

Готовимся к тематическому оцениванию по теме

113

7. Чему равен угловой коэффициент прямой, изображённой на рис. 107?

8. Каково уравнение прямой, изображённой на:

а°) рис. 108, а); б°) рис. 108, б); в) рис. 108, в)?

9°. ВОЗрастает или убывает линейная функ-

ция у = – 2(1 – 3х)?

10°. Сколько нулей имеет функция:

в) у = 0,5х2

– 2х + 2?

а) у = 0,5х2 – х + 1;

б) у = 0,5х2 + х – 1;

11°. Каковы координаты вершины параболы:

а) у = –(х + 2)2;

б) у = х2 – 4х + 3?

12.

Каковнаибольшийпромежуток,накоторомвозрастаетфункция:

а) у = 2х2 – 3х + 4;

б) у = –х2 + 4х – 1?

– 8х + 1:

13.

Чему равно наименьшее значение функции у = 2х2

а) в ее области определения; б) на промежутке [0; 1]?

14.

Каково множество значений функции:

– 6х + 2?

а) у = 3х2 – 6х + 2;

б) у = –3х2

15°.На каком из рис. 109, а) – г), изображен график функции y = x + 2?

16°.На

каком из рис. 110, а)–г) изображен график функции

у =

х4 + 2?

114

Функции, их свойства и графики

17°.Сколько значений имеет корень четвертой степени из числа:

а) 3; б) –3?

18°.Сколько значений имеет корень пятой степени из числа: а) 3;

б) –3?

19°.Какое из выражений не имеет смысла:

а) 3 −2;

б) 4 −2;

в) 4 (−1)2 ?

20.Верно ли, что: а) 4 a4 = a; б) 3 a3 = a?

21.Чему равно значение выражения:

а°) (3 −2)3 ;

б) 3 (−2)3 ;

в°) 4 34 ;

г) 4 (−3)4 ;

4

1

5

3

128

д°) (4 3)

;

е°)

3 121 3 11;

ё°)

−25

;

ж)

?

4

3

2

22.

Какие из следующих чисел являются иррациональными:

а) 3 16;

б)

3 9;

в) 3 64;

г)

4 16;

д)

4 125;

е) 5 32?

23.

Какие из следующих функций убывают:

а) y = x−

5

б) y = x−

3

в)

5

;

3

?

3 ;

5 ;

y = x3

г) y = x5

24.

Верно ли неравенство:

> (0,2)-2,5;

в) (0,5)0,4 > (0,2)0,4?

а) (0,5)2,5

> (0,2)2,5;

б) (0,5)-2,5

1

3

1

25°.Вычислите:

36

−

3

3

.

2

8

26. Представьте в виде степени выражение:

а) (a4 )−	1			1		2		1
	2	;	б)	x3	: x−	3	;	в) (5 a2 )2 .

Готовимся к тематическому оцениванию по теме

115

Ответы к заданиям для самоконтроля

1.Нет. 2. Нет. 3. 0; − 1 ; (1;0). 4. а) R; б) (−∞; −1) (−1;1) (1;+∞). 5. Чётная:

2

б); нечётная: г). 6. а) [–2; 5]; б) ни чётной, ни нечётной; в) 3; г) f(x) > 0 при

х (–2; – 1) (3; 5); f(x) < 0 при х (– 1; 3); д) 4; е) [– 2; 1]; ё) 1 и – 2; ж) 2. 7. 3. 8. а) у = 3; б) у = 2х + 2; в) у = –х + 2. 9. Возрастает. 10. а) 0; б) 2; в) 1. 11. а) (–2; 0);

б) (2; –1). 12. а)	3			; б)	(−∞;2]. 13. а) –7; б) –5. 14. а) [−1; +∞); б)	(−∞;5].
		4	; +∞

15. Рис. 109, б). 16. Рис. 110, в). 17. а) 2; б) 0. 18. а) 1; б) 1. 19. б). 20. а) Нет; б) да. 21. а) –2; б) –2; в) 3; г) 3; д) 3; е) 11; ё) –8. 22. а), б), г), д). 23. а) и б).

	Образец контрольной работы № 1
1. На рис. 111 изображен график функции
	у = f(x). Найдите:
	1°) область определения функции;
	2°) промежутки ее возрастания и убыва-
	ния;
	3°) наибольшее и наименьшее значения
	функции;
	4°) множество ее значений;
	5°) количество корней уравнения f(x)= 0,5;
	6) нули функции у = f(2x).
2. Дана функция f(x) = (x – 1)3.
	1°) Найдите область определения функции.
	2°) Каково ее значение в точке x = 3 2 +1?
	3°) Найдите точки пересечения графика функции с осями ко-
	ординат.
	4°) Постройте ее график.
	5) Сколько корней имеет уравнение f(x) = x2?
3.	Вычислите:		1 7 +	2 6;
	1	2)			3)		16 6	16.
	1°) 8−3 23 ;					3
			9	27

116	Функции, их свойства и графики
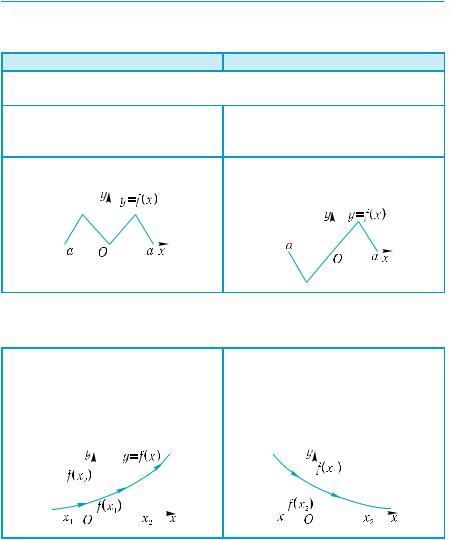
Чётные и нечётные функции
	Таблица 8
Чётные функции	Нечётные функции

Область определения функции симметрична относительно начала координат.

f(– x) = f(x) для произвольного х f(– x) = – f(x) для произвольного
из области определения функ-						х из области определения фун-
ции.						кции.
График функции симметричен						График функции симметричен
относительно оси у.						относительно начала коорди-
						нат.

	Таблица 9
Возрастающая функция:	Убывающая функция:
x2 > x1 f(x2) > f(x1)	x2 > x1 f(x2) < f(x1).
(большему значению аргумента (большему значению аргумента
Монотонные функции

из области определения функиз области определения функ-
ции соответствует большее зна-						ции соответствует меньшее зна-
чение функции).						чение функции).

Готовимся к тематическому оцениванию по теме

117

Чтение графика функции

Область определения функции — проекция графика на ось х.

Таблица 10

D(f) = [a; b]

Нули функции – абсциссы точек пересечения графика функции с осью х.

Промежутки

знакопостоянства функции —

промежутки, на которых функция принимает положительные или отрицательные значения.

Множество значений функ-

ции — проекция графика на ось у.

Промежутки монотонности функции — промежутки, на которых функция возрастает или убывает.

x1, x2, x3 – нули функции f(x) > 0 x [a; x1) (x2; x3) f(x) < 0 x (x1; x2) (x3; b]

E(f) = [m; M]

f(x) x [x1,x2 ]

f(x) x [a,x1 ],x [x2,b]

118					Функции, их свойства и графики
Определение степени с рациональным показателем
					Таблица 11
Степень с натуральным	n N,n >1 an = a a ... a. а1 = а.
показателем					n pаз
Степень с нулевым пока-	а0 = 1, а ≠ 0.
зателем
Степень с целым отрица-	a	−n	1		,a ≠ 0, n N .
тельным показателем			=
				an
Степень с дробным		m	= n am , а > 0, m Z, n N, n > 1.
показателем	a n

Свойства степени с рациональным показателем

Произведение степеней с одинаковыми основаниями

Частное от деления степеней с одинаковыми основаниями

Возведение степени в степень Степень произведения Степень частного

Таблица 12

ax ay = ax +y , x, y Q, a > 0.

ax : ay = ax −y , x, y Q, a > 0.

(ax )y = axy , x, y Q, a > 0. (ab)x = ax bx , x Q, a,b > 0.

a x			ax		, x Q, a,b > 0.
		=	b	x
b

Арифметический корень n-ой степени и его свойства

				Таблица 13
Определение	а≥0,n N,n > 1 n a ≥ 0,(n a )n = a.
Арифметический корень из	а ≥ 0, b ≥ 0 n ab = n a n b.
произведения
Арифметический корень из	a		n a
дроби	а ≥ 0, b > 0 n b	=		.
			n b
Арифметический корень из	а ≥ 0, n, k N, n, k > 1
арифметического корня	n k a = nk a.
Основное свойство арифме-	а ≥ 0, n, m, k N, n, m, k > 1
тического корня	nk amk = n am .

Параллельность

прямых и плоскостей

Мы начинаем изучение геометрии пространства, или стереометрии (от греческих «στερεοζ» — пространственный, «μετρeα» — измеряю). Возникнув из потребностей практики, постоянно развиваясь, геометрия является одной из важнейших математических наук для описания окружающего мира. Знание планиметрии, то есть геометрии плоскости, недостаточно для моделирования реальных объектов. Вместе с тем, при изучении стереометрии мы будем опираться на планиметрию, используя ее понятия, факты, методы. Так, метод построения стереометрии — аксиоматический — уже использовался

в планиметрии. Как и в планиметрии, основными объектами изучения будут геометрические фигуры — идеализированные образы реальных физических объектов. Некоторые из этих фигур (точка, прямая, треугольник и т. п.) уже изучались в геометрии, хотя раньше они рассматривались на плоскости. С другими «неплоскими» фигурами — такими, как куб, параллелепипед, шар, — мы встречались и в математике, и в других науках, и непосредственно в практической деятельности. Стереометрия изучает свойства пространственных фигур и отношения между ними.

В этом разделе мы рассмотрим варианты взаимного расположения прямых, прямой и плоскости, двух плоскостей. Особое внимание будет уделено отношению параллельности между прямыми и плоскостями, имеющему важное теоретическое и прикладное значение. Будут также рассмотрены основные правила и законы изображения фигур, дающие возможность распознать пространственную фигуру и выявить ее свойства по рисунку.

Готовимся к изучению

темы «Параллельность прямых и плоскостей»

Параллельность и перпендикулярность прямых на плоскости

Таблица 14

Две прямые называются перпендикулярными, если они пересекаются под прямым углом. Отрезки, лучи считаются перпендикулярными, если они принадлежат перпендикулярным прямым.

Две прямые на плоскости, не имеющие об-

щих точек, называются параллельными.

Соответственно и лучи, отрезки называются

параллельными, если они лежат на парал-

лельных прямых.

Признаки параллельности прямых

Две прямые, перпендикулярные третьей, параллельны между собой.

a b, a c b || с

Две прямые, параллельные третьей, параллельны между собой.

a || b, с || b a || с

Готовимся к изучению темы «Параллельность прямых и плоскостей»

121

Треугольник,его элементы и виды

Таблица 15

Треугольником называется часть плоскости, ограниченная тремя отрезками, соединяющими три точки плоскости, не лежащие на одной прямой.

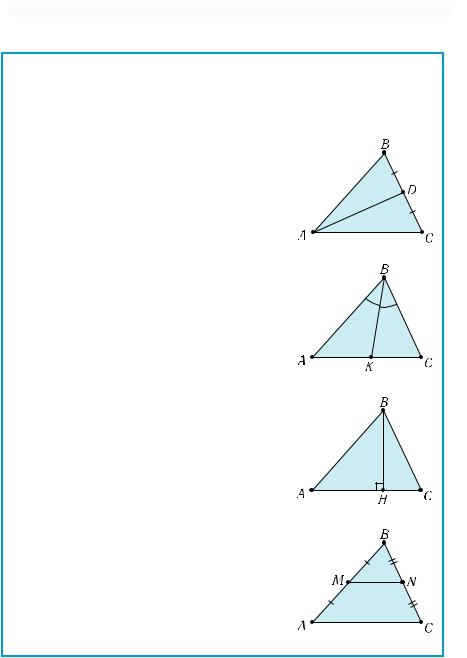
Важнейшие отрезки треугольника

Медиана треугольника — отрезок,

соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника — от-

резок биссектрисы угла (луча, выходящего из вершины угла и делящего его пополам) треугольника, соединяющий вершину треугольника с точкой на противоположной стороне треугольника.

Высота треугольника — перпенди-

куляр, проведенный из вершины треугольника на прямую, содержащую его противоположную сторону.

Средняя линия треугольника —

отрезок, соединяющий середины двух сторон треугольника.

AD — медиана

ВK — биссектриса

ВН — высота

MN — средняя линия

122	Параллельность прямых и плоскостей

Равенство треугольников

Таблица 16

Треугольникиназываютсяравнымимеждусобой,если

их можно совместить перемещением (движением).

Обозначается равенство треугольников АВС и А1В1С1 так:

∆АВС = ∆А1В1С1.

Признаки равенства треугольников

1. Если две стороны и угол, лежащий между ними, од-

ного треугольника равны соответственно двум сторонам и углу, лежащему между ними, второго треугольника, то такие треугольники равны.

АВ = А1В1, АС = А1С1, А = А1 ∆АВС = ∆А1В1С1

2. Если сторона и два прилежащих к ней угла одного

треугольника соответственно равны стороне и двум прилежащим к ней углам второго треугольника, то такие треугольники равны.

АВ = А1В1, А = А1, В = В1 ∆АВС = ∆А1В1С1

3. Если три стороны одного треугольника соответс-

твенно равны трем сторонам второго треугольника, то такие треугольники равны.

АВ = А1В1, ВС = В1С1, АС = А1С1 ∆АВС = ∆А1В1С1

Готовимся к изучению темы «Параллельность прямых и плоскостей»

123

Подобие треугольников

Таблица 17

Два треугольника называются подобными, если в них соответствующие углы равны, а соответствую-

щие стороны пропорциональны.

Обозначается подобие треугольников АВС и А1В1С1 так:

∆АВС " ∆А1В1С1.

Признаки подобия треугольников

1. Если два угла одного треугольника равны двум уг-

лам второго треугольника, то такие треугольники подобны.

А = А1, В = В1 ∆АВС " ∆А1В1С1

2. Если две стороны одного треугольника пропорци-

ональны двум сторонам второго и углы между ними равны, то такие треугольники подобны.

AB = AC , А = А1 ∆АВС " ∆А1В1С1

A1B1 A1C1

3. Если три стороны одного треугольника пропорцио-

нальны трем сторонам второго, то такие треугольники подобны.

AB	=	AC	=	BC	∆АВС " ∆А В		С	1
A1B1		A1C1		1		1
				B1C1

124	Параллельность прямых и плоскостей

Пропорциональные отрезки

Таблица 18

Теорема Фалеса.

Еслинаоднойиздвухпрямыхотложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекают на второй прямой равные между собой отрезки.

Теоремаопропорциональныхот-

резках. Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

BC || B1C1 AC1 = AB1 C1C B1B

Теорема, обратная теореме о пропорциональных отрезках.

Если прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки, то эти прямые — параллельны.

AC1 = AB1 BC || B1C1 C1C B1B

Средняя линия треугольника параллельна одной из его сторон, а ее длина равна половине длины этой стороны.

AE = 12 AB, CF = 12 BC

EF || AC, EF = 12 AC

Готовимся к изучению темы «Параллельность прямых и плоскостей»

125

Биссектриса внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилегающим сторонам, а ее точки равноудалены от сторон угла.

ABD = DBC

DM = DN, DCAD = BCAB

Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

АМ = MB, BN = NC,

CK = KA

PNAP = PKBP = PMCP = 12

Равнобедренный треугольник

Таблица 19

Треугольникназываетсяравнобедренным,еслионимеет две равные стороны. Эти стороны называются бо- ковыми,ихобщаявершина—вершинойравнобедренно- го треугольника, третья сторона — его основанием.

Свойства

1.Углы при основании равнобедренного треугольника равны между собой.

2.Медиана, биссектриса, высота, проведенные из вершины равнобедренного треугольника, совпадают.

3.Биссектрисы углов при основании равнобедренного треугольника равны между собой.

4.Медианы, проведенные к равным сторонам равнобедренного треугольника, равны между собой.

5.Высоты, проведенные к равным сторонам равнобедренного треугольника, равны между собой.

126	Параллельность прямых и плоскостей

Геометрия четырехугольников

Таблица 20

Определения

Параллелограммом называется четы-

рехугольник, противоположные стороны которого параллельны.

Если в параллелограмме равны смежные стороны, то он называется ромбом.

Параллелограмм с прямыми углами назы-

вается прямоугольником.

Прямоугольник с равными сторонами на-

зывается квадратом.

Трапецией называют четырехугольник, у которого только две стороны (основания) параллельны. Другие две стороны называют боковыми. Отрезок, соединяющий середины боковых сторон, называют средней линией трапеции.

Свойства

В параллелограмме противоположные стороны и углы равны между собой.

Диагонали параллелограмма точкой пересечения делятся пополам.

Диагонали прямоугольника равны между собой.

Диагонали ромба перпендикулярны. Они являются биссектрисами углов ромба.

тест для диагностики

готовности к изучению темы «Параллельность прямых и плоскостей»

1.	Углы треугольника относятся, как 2 : 3 : 5. Этот треугольник ...
	A.	может быть любым.				Б. остроугольный.
	B.	тупоугольный.				Г.	прямоугольный.
2.	Сторонытреугольникавыражаютсяразличнымицелымичис-
	лами; одна сторона равна 3 м, вторая — 2 м. Третья сторона
	может равняться ...					В. 5 м.		Г. 2 м.
	А.	1 м.			Б. 4 м.
3.	Из	одной			точки, расположенной вне прямой,					проведен к
	этой прямой перпендикуляр длиной 8 см и наклонная, проек-
	ция которой на прямую равна 6 см. Длина наклонной равна ...
	А.	28 см.			Б. 9 см.		В. 10 см.
	Г. величине, отличной от приведенных.
4.	В прямоугольном треугольнике один из углов равен 60°, а ги-
	потенуза — 20 см. Чему равен меньший катет?
	А. 10		3	см. Б. 8 3 см.		В. 10 см.		Г. 8 см.
5.	Точка		О	— середина отрезка AB,			FD ||AB. Срав-
	ните площади треугольников					ADC и FCB, рав-
	ные S		и S		соответственно.	В. S = S .
	А. S < S			. 1	Б. S > S .
			1		1		1
	Г. Сравнить невозможно.
6.	В равнобедренном треугольнике высота, проведенная к его
	основанию, и боковая сторона равны, соответственно, 12 см
	и 13 см. Основание равно ...						313 см.	Г. 2 см.
	А. 5 см.				Б. 10 см.	В.
7.	Тупой угол параллелограмма равен 140°. Угол между высота-
	ми параллелограмма равен ...					В. 40°.		Г. 160°.
	А.	80°.			Б. 20°.
8.	Площадь параллелограмма ABCD равна S,							M	— середина
	стороны BC. Чему равна площадь треугольника								АВМ?
	А.	2 S .			Б. 1 S .	В.	3 S .	Г.	1 S .
		3			2		4		4

128	Параллельность прямых и плоскостей

9.Биссектриса угла С в параллелограмме ABCD делит сторону АВ на отрезки 7 см и 14 см (считая от вершины В). Периметр параллелограмма равен ...

56 см. Б. 70 см. В. 42 см. Г. 35 см.

Два неравных отрезка точкой пересечения делятся пополам. Их концы последовательно соединены. Полученный четырехугольник является ...

параллелограммом. Б. ромбом. прямоугольником. Г. квадратом.

Сторона ромба равна 10 см, одна из диагоналей — 16 см. Вторая диагональ равна ...

	А. 6 см.	Б.	156 см.	В.	356 см.	Г. 12 см.
12.	Через точку данной окружности проведены диаметр и хорда,
	равная радиусу. Угол между ними равен ...					60°.
	А. 30°.		Б. 45°.		В.
	Г. величине, отличной от приведенных.
13.	Через точку, лежащую вне окружности, проведены к ней две
	взаимно перпендикулярные касательные. Длины отрезков
	касательных от данной точки до точек касания равны 8 см.
	Радиус окружности равен ...
	А. 4 2 см.		Б. 8 см.		В. 4 см.
	Г. величине, отличной от приведенных.
14.	Наибольшее и наименьшее расстояния от точки вне окруж-
	ности до точек этой окружности равны 8 см и 2 см. Радиус
	окружности равен ...			В. 10 см.		Г. 5 см.
	А. 3 см.	Б.	6 см.
15.	Геометрическое место точек, равноудаленных от вершин тре-
	угольника, является точкой пересечения ...
	A. высот треугольника.			Б.	медиан треугольника.
	B. биссектрис треугольника.
	Г. срединных перпендикуляров к сторонам треугольника.
16.	Внутренний диаметр трубы равен 80 мм, а толщина стенки —
	4 мм. Внешний диаметр ее равен ...					Г. 72 мм
	А. 84 мм.	Б.	88 мм.	В.	76 мм.
17.	Боковая сторона и основание равнобедренного треугольника
	не могут быть пропорциональными числам ...
	А. 3 и 5.	Б.	3 и 4.	В.	2 и 3.	Г. 1 и 2.