2298 ЭИ

BC

= 25, BA =

162 + 122 =

256 + 144 = 20 .

cos α =

=

16 7 + 12 24

=

400

BA

BA

= 0,8 .

BA

BC

20 25

500

α = аrcсos 0,8 = 36°50′ (если воспользоваться калькулятором или компьютером, то результат может быть записан в виде 36,87°).

7. Для нахождения координат середины отрезка АС воспользуемся формулой (5.10), где λ = 1. Имеем

xN =

3 + (−6)

= −

3

= −1,5; уN

=

1+ 13

=

14

= 7

N(−1,5; 7) .

2

2

2

2

8. Координаты точки М, найдем по формуле (5.10), где λ = 2 / 3:

3 +

2

(−13)

17

1+

2

(− 11)

19

xM =

3

= −

= −3,4 ; yM =

3

= −

= −3,8 .

1+

2

5

1+

2

5

3

3

Окончательно:

M (−3,4; − 3,8) .

прямой ВС:

Ответ:

BC

=

25;

уравнение

24x − 7 y + 235 = 0 ;

уравнение

прямой АD:

7x + 24 y − 45 = 0 ; АD = 12 ;

S = 150 (кв. ед.); α = 36°50′; N(−1,5; 7) ; M (−3,4; − 3,8) . v

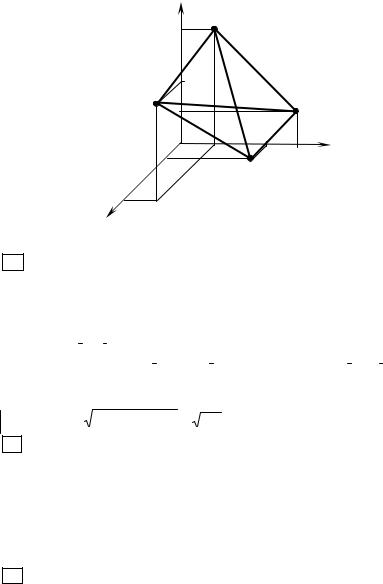
2 Задание 7 . По четырем заданным точкам А1(4, 2, 5), А2(0, 7, 2), А3(0, 2, 7), А4(1, 5, 0) построить пирамиду и средствами векторной алгебры найти: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) площадь грани А1А2А3; 4) объем пирамиды А1А2А3А4; 5) уравнение прямой А1А2; 6) уравнение

плоскости А1А2А3.

Чертеж пирамиды приведен на рисунке 6.2.

1. Найдем координаты и длину вектора A1A2 по формулам (5.1), (5.2)

A1 A2 = (0 − 4, 7 − 2, 2 − 5) = (− 4, 5, − 3),

A1 A2 = (− 4)2 + 52 + (− 3)2 = 16 + 25 + 9 = 50 = 5 2 .

2. Для определения угла ϕ, вычислим координаты и модули векторов, направленных по сторонам этого угла по формулам (5.1) и (5.2):

A1 A2 = (− 4, 5,−3), A1 A4 = (1− 4, 5 − 2, 0 − 5) = (−3, 3,−5) ;

A1 A4 = (− 3)2 + 32 + (− 5)2 = 9 + 9 + 25 = 43 .

Угол определим по формуле (5.4)

	cos ϕ =	A1 A2	A1 A4	=	(−4)(−3) + 5 3 + (−3)(−5)	=	42	≈ 0,91 .
		A1 A2	A1 A4		5 2 43		5 2 43
					41

	z	A3
	7
		5
A1	2	A2
	0

1	2	5	7	у
		A4
4
х	Р и с у н о к	6.2

По таблицам находим ϕ = 24°30′ .

3. Для вычисления площади грани А1А2А3 воспользуемся свойствами векторного произведения двух векторов, на которых построен треугольник А1А2А3, и формулой (5.5):

		S =		1		a ×			=	1								×					,							= (–4, 5,–3),							= (−4, 0, 2)	,
								b						A A					A A							A A									A A
				2						2				1		2				1		3				1	2					1				3
							i				j
														k			= i				5		− 3		− j				− 4		− 3			− 4		5
A A		×	A A			=	− 4 5							− 3
																																+ k					=10i + 20 j + 20k			,
1	2	1		3																	0		2						− 4		2			− 4		0
							− 4			0		2

A A		×	A A		= 102 + 202 + 202 = 900 = 30 S = 30 / 2 = 15 (кв. ед.).
1	2	1		3

4. Для вычисления объема воспользуемся формулой смешанного произведения (5.6):

				V =	1			(																	)			,
									A A								A A					A A
					6			1					2				1	3	1				4
V =	1		− 4	5	− 3								1											2
			− 4	0		2						=					− 70				= 11							(куб. ед.).
	6		− 3	3	− 5								6										3

5. Для определения уравнения прямой А1А2 воспользуемся уравнением

(5.9). Имеем

	x − 4	=	y − 2	=	z − 5	,
	0 − 4		7 − 2		2 − 5

окончательно получаем уравнение прямой А1А2

42

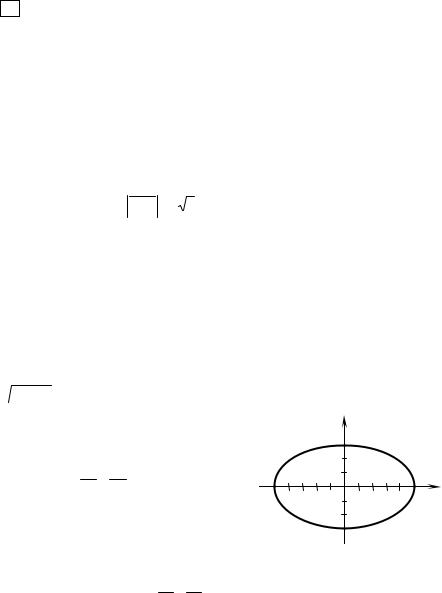
x − 4	=	y − 2	=	z − 5	.
− 4		5
				− 3

6. Уравнение плоскости А1А2А3 запишем в форме уравнения плоскости, проходящей через три точки по формуле (5.8)

	х− 4	y − 2 z − 5			= 0		x − 4 y − 2 z − 5				= 0
	0 − 4	7 − 2	2 − 5				− 4	5	− 3
	0 − 4	2 − 2	7 − 5				− 4	0	2

(x − 4)

5

− 3

− (y − 2)

− 4

− 3

+ (z − 5)

− 4

5

= 0

0

2

− 4

2

− 4

0

(x − 4)10 − (y

− 2) (−

20)+ (z −

5) 20 = 0

10x + 20 y + 20z − 180 = 0 .

Разделим обе части уравнения на 10, окончательно уравнение плоскости А1А2А3 примет вид x + 2y + 2z – 18 = 0.

Ответ: A A = 5		2 ; ϕ = 24°30′ ;					S	= 15 (кв. ед.); V = 11	2
1	2							3
(куб. ед.); уравнение прямой А1А2:		x − 4	=	y − 2	=	z − 5		; уравнение плоскости
		− 4		5
							− 3

А1А2А3: x + 2y + 2z – 18 = 0. v

2 З а д а н и е 8 . Составить канонические уравнения: а) эллипса, зная, что расстояние между фокусами равно 8, а малая полуось равна 3; б) гиперболы, если она проходит через точку (–5, 3) и имеет эксцентриситет ε =

2; в) найти координаты фокуса и уравнение директрисы параболы x2 = 8y .

Р е ш е н и е .

а). По условию 2с = 8 , т. е. с = 4, b = 3 . Воспользуемся формулой

c = a2 − b2 , откуда a2 = b2 + c2 :

a2 = 32 + 42 = 25 или a = 5.

Тогда каноническое уравнение эллипса примет вид (5.14)

x2 + y2 = 1 . 25 9

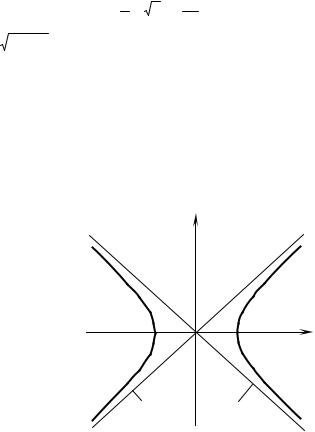
Выполним чертеж (рисунок 6.3).

б). Так как гипербола проходит через точку (–5, 3), то координаты этой точки удовлетворяют каноническому уравнению гиперболы (5.15), имеем

а252 − b92 = 1 .

			у		x	2	+	y	2	= 1
			3
				25				9
			2
–5	–4	–2	0	2			4	5		х
			–2
			–3
		Р и с у н о к		6.3

(6.1)

43

По условию

ε =

c

=

2

c2

= 2 .

Далее, используя формулу

a

a2

с = а2 + b2 , получаем

a2 + b2

= 2 1 +

b2

= 2

b2

= 1 a2 = b2 .

a2

a2

a2

Подставим последнее равенство в (6.1) и получим

25

−

9

= 1

16

= 1 a2 = 16 .

a2

a2

a2

Окончательно имеем: x2 − y2 = 16

x2

−

y2

= 1 .

16

16

Получили равностороннюю гиперболу. Выполним чертеж (рисунок 6.4).

y

x2

y2

−

= 1

16

16

4

x

–4

0

4

–4

у = – х

у = х

Р и с у н о к 6.4

в). Из канонического уравнения параболы (5.16) заключаем, что 2р = 8р = 4, р / 2 = 2. Таким образом, уравнение директрисы запишется в виде у = –2, фокусом является точка F(0, 2).

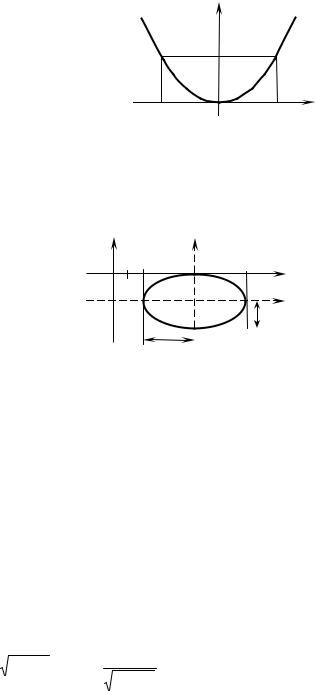
Выполним чертеж (рисунок 6.5). v

2 З а д а н и е 9 . Привести к каноническому виду уравнение кривой

второго порядка, определить тип линии и построить эту кривую

4х2 + 9у2 – 40х + 36у + 100 = 0.

Решение. Так как отсутствует член, содержащий произведение ху (В = 0), то поворота осей нет. Выделим полные квадраты. Для этого преобразуем уравнение

4(x2 − 10x) + 9( y2 + 4 y) = −100 ,

4(x2 −10x + 25) −100 + 9( y2 + 4y + 4) − 36 = −100 , 44

			y
				y = х2 / 8
4(x − 5)2 + 9( y + 2)2 = 36 .		4
Сделаем перенос начала координат
x′ = x − 5,
y′ = y + 2,
	–4		0		4	х
тогда начало новой системы координат будет в
		Р и с у н о к			6.5
точке O′(5, − 2) , а уравнение примет вид

4x′2 + 9 y′2 = 36 . Преобразуем полученное уравнение и получим уравнение эллипса с полуосями а = 3, b = 2:

x′2

+

y′2

= 1 .

9

4

Итак, в системе

координат x′O′y′

y

y′

уравнение кривой принимает канони-

O 1 2

3

4 5 6

7 8

ческий вид. Оси координат O′x′ и O′y′

x

параллельны осям координат Ох и Оу

–1

соответственно, а начало перенесено в

–2

O′

2 х′

точку O′(5, − 2) .

–4

Используя полученные в процессе

3

преобразования кривой данные, вы-

Р и с у н о к 6.6

полним построение кривой (рисунок

6.6). v

9

2 З а д а н и е

1 0 . Даны уравнения линии

r =

в полярной

5 + 4 cos ϕ

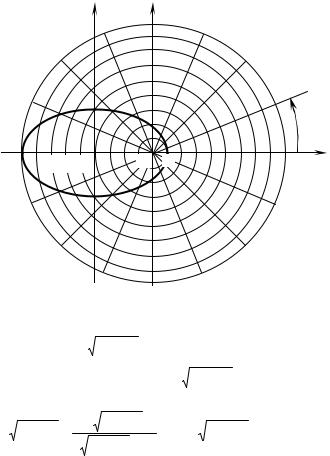
системе координат. Требуется: 1) построить линию по точкам на промежутке от ϕ = 0 до ϕ = 2π с шагом, равным π / 8; 2) найти уравнение линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) назвать линию, найти координаты центра и длины полуосей.

Р е ш е н и е . Составим таблицу 5 для вычисления значений r.

Таблица 5

ϕ	0	π / 8	π / 4	3π / 8	π / 2	5π / 8	3π / 4	7π / 8	π	…
c o s ϕ	1	0,92	0,71	0,38	0	–0,38	–0,71	–0,92	–1	…
r	1	1,04	1,15	1,38	1,80	2,59	4,14	6,90	9	…

Построим линию, учитывая, что cos(2π − ϕ) = cos ϕ (рисунок 6.7).

Для перехода в декартовую систему координат воспользуемся формулами

	r = x2 + y2 , cos ϕ =	x	.
		x2 + y2
	45

у ′

у

3

π / 8

–9

О′(–4, 0)

О 1 2 3 4 5 6 7 8 9 х, х′

–3

Р и с у н о к

6.7

Получим уравнение

9

x2 + y2

=

,

5 + 4

х

x2 + y2

которое после преобразований примет вид

x2 + y2 =

9 x2 + y2

5 x2 + y2 + 4x = 9

5 x2 + y2 + 4x

25(x2 + y2 ) = (9 − 4x)2 25x2 + 25 y2 = 81− 72x + 16x2

9x2 + 25y2 + 72x = 81 ,

9(x2 + 8x + 16) + 25y2 − 144 = 81

9(x + 4)2 + 25y2 = 225

(x +

4)

2

+

y2

= 1 .

25

9

Получили уравнение эллипса с центром в точке О′(–4; 0) и полуосями а = 5, b = 3 (рисунок 6.7).

Ответ: уравнение эллипса с центром в точке

О(–4; 0) и полуосями а = 5, b = 3. v

46

7 . З А Д А Н И Я Д Л Я К О Н Т Р О Л Ь Н О Й Р А Б О Т Ы № 3

З А Д А Н И Е № 1 1

Даны комплексные числа z1 и z2 (таблица 6).

а). Записать их в тригонометрической форме и отметить полученные числа на комплексной плоскости; б). Найти числа z1 + z2, z1 – z2, построить; в). Найти z1 z2, z1 / z2, записать в тригонометрической и алгебраической формах,

сравнить результаты; г). Найти z13 ; д). Найти 3 z2 , построить.

															Таблица 6
	№ варианта		z1				z2				№ варианта		z1				z2
	11.1.	2	3 + 2i					4			11.16.	− 3	3 + 9i				−4
							1	+ i									1− i
	11.2.	3 + 3i						8			11.17.	– 4 + 4i					−8
					1		+	3i							i		−	3
	11.3.	4 + 4		3i				4			11.18.	− 6 + 2		3i			−8
							3 + i										3	− i
	11.4.	−	3 + 3i					2			11.19.	−	3 −	3i			6
							1	− i									1+ i
	11.5.	– 2 + 2i						4			11.20.	3 – 3i					4
					1		−	3i							1		+	3i
	11.6.	− 3 +		3i				2			11.21.	− 4	3 − 4i				8
							3 − i										3	+ i
	11.7.	− 2	3 − 6i					8			11.22.	2	3 −	6i			6
					i		+ 3										1+ i
	11.8.	– 4 – 4i					12				11.23.	2 – 2i					8
							3i + 1								1		−	3i
	11.9.	−	3 − i					4			11.24.	3	3 −	3i			4
						2i		+ 2									3	− i
	11.10.	3	3 − 9i				−2				11.25.	4	3 +	4i			4
							1	− i								2 + 2i
	11.11.	1 – i					−4				11.26.	1 + i					12
							3 − i								1		+	3i
	11.12.		3 − i				−8				11.27.	3 + 3 3i					16
					1		−	3i									3	+ i

47

№ варианта

z1

z2

№ варианта

z1

z2

11.13.

3

3 +

3i

8

11.28.

−

12 + 6i

−6

i

+ 1

1− i

11.14.

2 + 2i

4

11.29.

– 5 + 5i

−8

3i + 1

3 − i

11.15.

2 + 2

3i

8

11.30.

6 + 2 3i

−

4

i

+

3

− 3

i

З А Д А Н И Е

№

1 2

Методом деформации и сдвигов построить графики функций.

12.1. а)

у = 2 cos(2x + 1) ;

b)

у = 2х−1 + 5 .

12.2. а)

у = 3sin(2x + 2) ;

b)

у = 3x+1 − 4 .

12.3. а)

у = −2 cos(3x − π / 6) ;

b)

у = 5x+ 2 − 3 .

12.4. а)

у = −3sin(2x + π / 6) ;

b)

у = ex−2 + 1 .

12.5. а)

у = 4 cos(2x + π / 6) ;

b)

у = ex−3 + 2 .

12.6. а)

у = 3sin(3x − π / 4);

b)

у = ex+3 − 4 .

12.7. а)

у = 2 cos(3x − π / 3) ;

b)

у = (1/ 2)x−1 + 3 .

12.8. а)

у = 3sin(2x − π / 3);

b)

у = (1/ 3)x+1 − 2 .

12.9. а)

у = −2sin(2x − π / 4) ;

b)

у = (1/ 4)x−2 + 1.

12.10. а)

у = −3cos(2x + π / 4);

b)

у = (1/ 5)х+ 2 − 3 .

12.11. а)

у = 4 cos(x / 2 − π / 3);

b)

у = е2− х + 1 .

12.12. а)

у = 3sin(x / 2 − 2π / 3);

b)

у = e3− x + 2 .

12.13. а)

у = −2 cos(3x − 3π / 4);

b)

у = 1− ех+1 .

12.14. а)

у = − sin(x / 2 + 5π / 6) ;

b)

у = 2 − ех−1 .

12.15. а)

у = 3cos(3x + π / 2) ;

b)

у = 3 − ех+ 2 .

12.16. а)

у = 4sin(2x − π / 6);

b)

у = 4 − ех−2 .

12.17. а)

у = 5cos(3x − 2π / 3);

b)

у = 2х+ 2 − 3 .

12.18. а)

у = −5sin(2x − π / 2) ;

b)

у = 3x−3 + 1 .

12.19. а)

у = 4 cos(1,5x − 2) ;

b)

у = 42− x + 2 .

12.20. а)

у = 3cos(1,5x + 1) ;

b)

у = 53− x −1 .

48

12.21.а) у = 2sin(1,5x − 1) ;

12.22.а) у = 3sin(1,5x + π / 3) ;

12.23.а) у = 4 cos(2x − 7π / 6);

12.24.а) у = 3sin(3x − π / 6);

12.25.а) у = 2 cos(2x − 3π / 4) ;

12.26.а) у = −2sin(2x − π / 4) ;

12.27.а) у = 5cos(2x − 1) ;

12.28.а) у = 3sin(3x − 2) ;

12.29.а) у = 4 cos(4x − π / 6) ;

12.30.а) у = 0,5sin(2x − π / 3) ;

b) у = е5− x + 2 .

b) у = (1/ 2)x−4 + 1. b) у = (1/ 3)x+1 + 4 . b) у = 2 x+ 2 − 3 .

b) у = ln(x + 4)−1 . b) у = ln(x − 2)+ 2 . b) у = 2 − ln(x −1) . b) у = 3 − ln(x + 2). b) у = 5 − ln(x − 3) . b) у = 1− ln(x − 4) .

З А Д А Н И Е № 1 3

Построить кривую, заданную параметрическими уравнениями по точкам, придавая t значения от t = 0 до t = 2π c шагом π / 10.

Преобразовать уравнения к уравнениям линии в декартовой системе координат. Определить вид и параметры кривой.

x = 2sin t,

y = cost −1.x = cos2 t − 2,

y = 3sin t.

x = 2sin t + 1,

13.3.y = 2 cost − 3.

x = 3sin t,

13.4.y = cost + 2.x = cos2 t + 3,

y = 2sin t.

x = 3sin t − 2,

13.6.y = 3cost + 4.

x = cos t,

13.7.y = 2 + sin t.x = 3 + sin 2 t,

y = 2 cos t.

x = 2 + 4sin t,

13.9.y = 3 + 4 cos t.

x = 4 cost + 1,

13.10.y = 2sin t.

x = sin 2 t + 1,

y = cost − 3.

x = 5sin t −1,

13.12.y = 3 + 5sin t.

x = 4 cos t − 2,

13.13.y = 3sin t.

x = 2 − sin 2 t,

y = cos t + 1.

x = 4sin t −1,

13.15.y = 4 cost + 3.

x = 3cost,

13.16.y = sin t + 2.

49

x = sin 2 t − 4,

13.17.

y = 2 cos t.

13.18.	x = 2sin t + 3,
	y = 2 cost.
13.19.	x = 3sin t + 1,
	y = 2 cost − 4.
	x = sin t + 1,
13.20.
	y = cos2 t + 3.
13.21.	x = 1− 3sin t,
	y = 2 + 3cos t.
13.22.	x = sin t	+ 1,
		− 3.
	y = cost
	x = 2 + cost,
13.23.
	y = sin 2 t + 1.

x = 1,5cost + 4,

13.24.y = 1,5sin t − 1.

x = 2 cost + 1,

13.25.y = 3sin t − 2.x = 1+ cost,

y = 2 + sin 2 t.

x =

13.27.y =

x =

13.28.y =x =

y =

x =

13.30.y =

1− 5sin t,

5cost + 3.

4 cost + 2, 3sin t −1. 1− cost, 2sin 2 t. cost − 3, 2sin t + 2.

З А Д А Н И Е № 1 4

Найти пределы функций.

	14.1. а)		lim	x2 − 6x + 8
				x2 − 8x + 12
			x→ x0
б)	lim	x2	− 3x + 2		;			в)
		5 − x −		x +
	x→2				1
	14.2. а)		lim	x2 − 5x + 6
				x2 − 9
			x→ x0
б)	lim	3x2 + 4x + 1				;		в)
				5 + 3x
	x→−1 x + 3 −
	14.3. а)		lim	3x2 − 2x − 8
				x2 + 3x − 10
			x→ x0
б)	lim	2x2 − 9x + 4			;			в)
		5 − x −		x −
	x→4				3
	14.4. а)		lim	6x2 + 13x + 7
				3x2 + 8x + 5
			x→ x0

при x0 = 3 ,								x0
x + 3						3x−5
lim						;
x→∞ x − 2
при x0 = 5 ,								x0
x − 4						2x+6
lim						;
x→∞ x + 4
при x0 = 6 ,								x0
4 x + 1 2 x								;
lim
			4 x
x → ∞
при x0 = 4 ,								x0

= 2 , x0 → ∞ ;
г) lim			1− cos x	.
x→0			5x2
= 3 , x0 → ∞ ;
г) lim		1− cos 3x			.
x→0			x2
= 2 , x0 → ∞ ;
г) lim	cos x − cos5 x					.
			x2
x→0

= −1 , x0 → ∞ ;

50