
- •Кафедра электротехники и электрических машин Лекция № 34 по дисциплине «Теоретические основы электротехники»
- •13.03.02 «Электроэнергетика и электротехника»
- •1.Уравнения максвелла в комплексной форме записи
- •Теорема единственности решения уравнений максвелла
- •Запаздывающие или обобщенные электродинамические потенциалы
- •2. Наклонное падение плоской волны
- •Излучение электромагнитных волн
- •Плоские электромагнитные волны. Основные определения
- •Уравнение плоской волны
- •Исследование волн
- •Распромтанение плоской волны.
- •Распространение плоской волны в хорошо проводящей среде
- •Поляризация электромагнитных волн
- •3. Явление поверхностного эффекта
- •Поверхностный эффект в цилиндрическом проводнике
- •Активное сопротивление и внутренняя индуктивность цилиндрического провода с учетом поверхностного эффекта
- •Теорема умова — пойнтинга
Теорема единственности решения уравнений максвелла
Покажем, что если при решении уравнений Максвелла для определенных начальных и граничных условий получены значения векторов поля Е и Н, то это решение единственное.
Предположим, что электромагнитное поле исследуется в определенной области пространства V, которая ограничена замкнутой поверхностью S. Параметры ε, µ и γ постоянны. Начальные и граничные условия заданы следующим образом. В момент t = 0 значения векторов Е и Н заданы во всех точках области V. На поверхности S известны касательные составляющие одного из векторов поля (предположим, Е) для всех моментов времени от 0 до t. Тогда уравнения Максвелла однозначно определяют векторы Е и Н в любой точке области V и в любой момент t.
Предположим противное, т. е. что существует другое решение уравнений Максвелла, причем значения векторов поля E1 и Н1 удовлетворяют перечисленным выше начальным и граничным условиям. Рассмотрим два новых вектора Е2 = Е -El , Н2 = Н –Н1. Очевидно, что Е2 и Н2 также являются решением уравнений Максвелла, но начальные и граничные условия для них будут несколько иными. При t = 0 во всех точках области V, E2 и Н2 должны равняться нулю, так как в этот момент Е = Е1 и Н = Н1. На поверхности S во все моменты времени от 0 до t касательная составляющая вектора Е2 также должна быть равна нулю. Следовательно, вектор Е2 может иметь на поверхности S только нормальную составляющую.
Применим к полю векторов Е2 и Н2 теорему Умова-Пойнтинга

На поверхности S произведение
[Е2Н2] dS = 0,
так как в любой точке граничной поверхности S направление Е2 совпадает с нормалью. Теорема Умова — Пойнтинга примет вид:

Первое слагаемое
этого выражения, равное мощности тепловых
потерь, может быть только величиной
положительной или равной нулю. Тогда
![]() должна быть или отрицательной величиной
(если
должна быть или отрицательной величиной
(если![]() убывает), или равной нулю (если
убывает), или равной нулю (если![]() =
const). Согласно начальным условиям в
момент t = 0 во всех точках рассматриваемой
области векторы поля равны нулю Е2 =0, Н2
= 0; следовательно, и
=
const). Согласно начальным условиям в
момент t = 0 во всех точках рассматриваемой
области векторы поля равны нулю Е2 =0, Н2
= 0; следовательно, и
![]()
Энергия не может принимать отрицательных значений, поэтому она должна оставаться равной нулю. Следовательно, векторы Е2 и Н2 равны нулю в любой момент t и в любой точке области V. Это значит, что Е –E1 =0, Н - Ht = 0, т. е. Е1 = Е и Н1 = Н и, следовательно, второе решение совпадает с первым.
Запаздывающие или обобщенные электродинамические потенциалы
Для определения
векторов Е и Н по заданныv
![]() и р необходимо решить полную систему
уравнений Мaксвелла
и р необходимо решить полную систему
уравнений Мaксвелла

Будем считать, что
параметры среды ε, µ, γ постоянны и
заданы. Искомые векторы Е и Н и заданные
величины
![]() и р зависят от трех пространственных
координат и времени.
и р зависят от трех пространственных
координат и времени.
Непосредственное решение уравнений Максвелла обычно связано с большими трудностями. Задачу можно упростить, если ввести вспомогательные функции φ и А пространственных координат и времени. Их называют обобщенными электродинамическими потенциалами.
Зависимости между Е и Н, а также между А и φ устанавливаются таким образом, чтобы основные уравнения поля приняли наиболее удобный для решения вид.
Положим
rot А = µаН = В,
что возможно, так как В соленоидальный вектор:
div В = 0.
Для однозначного определения вектора А надо задать еще и его дивергенцию, но подберем ее позже так, чтобы упростить полученные выражения.
Вектор А будем называть обобщенным векторным потенциалом.
Выразим напряженность магнитного поля через векторный потенциал
Н =
![]() rot А.
rot А.
П одставим
значение Н во второе уравнение Максвелла
одставим
значение Н во второе уравнение Максвелла
Заменив
последовательность дифференцирования
и сократив на![]() ,
,
получим:

Следовательно,
вектор
![]() потенциальный
и можно
потенциальный
и можно
найти такую скалярную функцию φ, для которой он служит градиентом:
![]()
Величину φ назовем обобщенным скалярным потенциалом. Мы связали уравнениями

векторы поля Е и Н с обобщенными потенциалами А и φ.
Для определения А и φ используем остальные уравнения электромагнитного поля.
Первое уравнение Максвелла можно записать следующим образом:
или

Обозначим
![]() Отметим, что величина
Отметим, что величина![]() имеет размерность скорости. Развернем
выражение ротора от ротора:
имеет размерность скорости. Развернем
выражение ротора от ротора:
![]()
или
![]()
Можно выбрать div А так, чтобы уравнение упростилось, положив
![]()
Тогда векторный потенциал определяется из уравнения
![]()
Е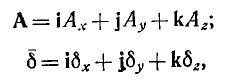 сли
записать это векторное уравнение в
прямоугольной декартовой системе
координат, то, считая, что
сли
записать это векторное уравнение в
прямоугольной декартовой системе
координат, то, считая, что
П олучим
три принципа Даламбера :
олучим
три принципа Даламбера :
Если в уравнение
div Е =
![]() подставить значение Е, то получим:
подставить значение Е, то получим:
![]()
или, так как div grad
φ =![]() , то
, то
![]()
Подставив выражение div А, получим:

Для определения скалярного потенциала также надо решить уравнение Даламбера.
Введя обобщенные потенциалы А и φ, мы свели уравнения Максвелла к четырем однотипным уравнениям Даламбера и этим значительно упростили задачу расчета электромагнитного поля.
Р ешения
уравнений Даламбера можно записать в
виде интегралов
ешения
уравнений Даламбера можно записать в
виде интегралов
Чтобы найти
скалярный потенциал в точке N в момент
t , надо разбить объем V на элементы dV,
определить величину заряда в этом
элементарном объеме
![]() в
момент
в
момент![]() (где R — расстояние от элемента объема
dV до точки N, a
(где R — расстояние от элемента объема
dV до точки N, a —
скорость распространения электромагнитной
энергии в диэлектрике с проницаемостью
εа и μa). Разделив этот заряд на 4πεаR и
проинтегрировав по всем элементарным
объемам в которых имеется заряд с
плотностью ρ, мы получим скалярный
потенциал в данной точке в момент t.
—
скорость распространения электромагнитной
энергии в диэлектрике с проницаемостью
εа и μa). Разделив этот заряд на 4πεаR и
проинтегрировав по всем элементарным
объемам в которых имеется заряд с
плотностью ρ, мы получим скалярный
потенциал в данной точке в момент t.
Аналогично определяются и проекции векторного потенциала. Важно отметить, что изменения свободных объемных зарядов и токов проводимости сказываются в различных точках поля не мгновенно, а спустя некоторое время R/υ, необходимое для того, чтобы электромагнитная волна прошла расстояние R. Поэтому потенциалы А и φ называются запаздывающими.
Для вакуума υ равно скорости света

В диэлектрике с проницаемостью ε при μ=1 величина скорости распространения электромагнитной энергии
![]()

Так как величина υ большая, то запаздывание скажется только при достаточно большом удалении точки от места расположения зарядов и токов и тем сильнее, чем больше это удаление.
В областях поля, не имеющих объемных зарядов и токов проводимости, уравнения, определяющие обобщенные потенциалы, примут вид:

Эти соотношения называются волновыми уравнениями.
При решении уравнений Даламбера и волновых уравнений должны быть учтены для каждой конкретной задачи начальные и граничные условия. Если область V, в которой исследуется поле, состоит из нескольких однородных сред, то на границах этих сред должны соблюдаться следующие соотношения:

В этих соотношениях:
σ — поверхностная плотность свободных зарядов на границе двух сред; η — плотность поверхностного тока на граничной поверхности.
