Перпендикулярность прямой и плоскости
Определение 3.3. 
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.
Теорема 3.1. Признак
перпендикулярности прямой и плоскости.
Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.
Сформулируем некоторые теоремы, устанавливающие связь между параллельностью и перпендикулярностью в пространстве.
Теорема 3.2. 
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой.
Теорема 3.3. 
Две прямые, перпендикулярные одной плоскости, параллельны между собой.
Теорема 3.4. 
Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой.
Теорема 3.5. 
Две плоскости, перпендикулярные одной прямой, параллельны между собой.
Докажите
эти теоремы самостоятельно, используя
такое свойство: если векторы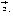 
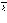коллинеарные
и 
то 
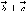
Определение 3.4. 
Перпендикуляром, проведенным из данной точки на данную плоскость, называется отрезок прямой, перпендикулярной данной плоскости, который соединяет данную точку с точкой плоскости.
|
|
|
Чертеж 3.2.4. |
Пусть AO – перпендикуляр к плоскости α (чертеж 3.2.4), O – основание перпендикуляра. Длина этого перпендикуляра AOназывается расстоянием от точки A до плоскости α. Отрезок, соединяющий точку A с любой точкой плоскости, отличной от O, называется наклонной (AB – наклонная, B – основание наклонной, BO – проекция наклонной на плоскость α, то естьBO = ПрαAB).
Теорема 3.6. 
Если из одной точки вне плоскости проведены к ней перпендикуляр и наклонные, то
-
длина перпендикуляра меньше длины любой наклонной;
-
наклонные с равными проекциями равны;
-
из двух наклонных большую длину имеет та, у которой больше проекция.
Теорема 3.7. О
трех перпендикулярах.
Для того, чтобы прямая на плоскости была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна ортогональной проекции наклонной на плоскость.
Перпендикулярность двух плоскостей
|
|
|
Чертеж 3.3.1. |
Определение 3.5. 
Пусть
прямая a является
линией пересечения плоскостей α и β (чертеж 3.3.1).
Пусть плоскость γ, перпендикулярная
прямой a,
пересекает плоскости α и β по
прямым m и n,
которые взаимно перпендикулярны, то
есть γ 
α = m, γ 
β = n и m 
n.
Такие плоскости α и β называются взаимно
перпендикулярными.
Это определение не зависит от плоскости γ. Действительно, если провести другую плоскость δ, перпендикулярную прямой a, то δ || γ.
Пусть δ 
α = m', δ 
β = n'.
По теореме о следах m' || m и n' || n.
Угол, образованный прямыми m' и n',
и угол, образованный прямыми m и n,
равны как углы с соответственно
параллельными и одинаково направленными
сторонами.
Теорема 3.8. Признак
перпендикулярности двух плоскостей.
Пусть a 
α, a 
β,
тогда β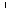 
α.
То есть, если плоскость β содержит
прямую a,
перпендикулярную плоскости α, то
плоскости α и β перпендикулярны.
Теорема 3.9. 
Пусть α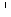 
β, α 
β = a, b 
a, b 
β,
тогда b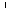 
α.
То есть прямая b,
лежащая в одной из взаимно перпендикулярных
плоскостей β и перпендикулярная
линии пересечения a этих
плоскостей, перпендикулярна и другой
плоскости α.
Теорема 3.10. 
Если плоскости α и β взаимно перпендикулярны, и к плоскости α проведен перпендикуляр, имеющий общую точку с плоскостью β, то этот перпендикуляр лежит в плоскости β.
Теорема 3.11. 
Пусть
плоскости α и β перпендикулярны
плоскости γ и пересекаются по
прямой a,
тогда a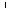 
γ.
Основные понятия
Определение 4.1. 
Многогранником в трехмерном пространстве называется совокупность конечного числа плоских многоугольников такая, что
-
каждая сторона любого из многоугольников есть одновременно сторона другого (но только одного), называемого смежным с первым по этой стороне;
-
от любого из многоугольников, составляющих многогранник, можно дойти до любого из них, переходя по очереди от одного многоугольника к другому, смежному с ним.
Многоугольники,
из которых состоят многогранники,
называются гранями,
их стороны – ребрами,
а их вершины –вершинами многогранника.
|
|
|
Рисунок 4.1.1. |
Определение 4.2. 
Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой его грани.
Из этого определения следует, что все грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Поверхность выпуклого многогранника состоит из граней, которые лежат в разных плоскостях. При этом ребрами многогранника являются стороны многоугольников, вершинами многогранника – вершины граней, плоскими углами многогранника – углы многоугольников-граней.