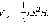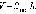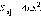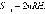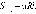- •Расстояние между точками
- •Уравнение прямой линии
- •Аксиомы стереометрии
- •Параллельность прямых
- •Параллельность прямой и плоскости
- •Параллельность двух плоскостей
- •Угол между двумя скрещивающимися прямыми
- •Перпендикулярность прямой и плоскости
- •Перпендикулярность двух плоскостей
- •Определение правильного многогранника
- •Параллелепипед
- •Пирамида
- •Цилиндр
- •Вписанные и описанные многогранники
- •Определение объема тела
- •Объем пирамиды
- •Объем цилиндра и конуса
- •Вычисление объемов тел вращения
- •Площади поверхности цилиндра, конуса, шара
Объем пирамиды
Лемма 6.1. 
Две пирамиды, имеющие равные высоты и равновеликие основания, имеют равные объемы.
Теорема 6.5. 
Объем
пирамиды равен
одной трети произведения площади
основания на высоту: 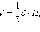 где S –
площадь основания, H –
высота пирамиды.
где S –
площадь основания, H –
высота пирамиды.
Теорема 6.6. 
Объем V усеченной
пирамиды может быть найден по
формуле 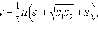 где H –
высота усеченной пирамиды, S1и S2 –
площади ее оснований.
где H –
высота усеченной пирамиды, S1и S2 –
площади ее оснований.
Объем цилиндра и конуса
Найдем объем цилиндра, конуса и усеченного конуса. Пусть H – высота, R – радиус цилиндра или конуса.
Теорема 7.1. 
Объемы цилиндра и конуса равны соответственно
|
|
|
|
Объем любого цилиндра можно найти по формуле
|
|
Объем любого конуса можно найти по формуле
|
|
Теорема 7.2. 
Объем
усеченного конуса равен 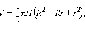 где R и r –
радиусы оснований усеченного конуса.
где R и r –
радиусы оснований усеченного конуса.
Вычисление объемов тел вращения
Укажем общий способ вычисления объемов тел вращения. В частности, вычислим объем шара и его частей.
|
|
|
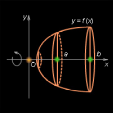
Рисунок 7.2.1. |
Пусть криволинейная трапеция, то есть фигура, ограниченная осью Ox, прямыми x = a, x = b и графиком непрерывной возрастающей неотрицательной функции y = f (x), вращается вокруг оси Ox (рис. 7.2.1), вследствие чего образуется тело вращения. Сечение этого тела плоскостью, перпендикулярной оси Ox, есть круг или точка. На промежутке (a; b) выберем точку x. Сечение, проведенное через эту точку перпендикулярно оси Ox, есть круг площадью S (x) = πf 2 (x). Объем части тела вращения, ограниченной сечениями, проведенными через точки a и x, обозначим через V (x), а объем данного тела вращения – через V.
Теорема 7.3. 
Объем тела вращения равен
|
|
|
|
Теорема 7.4. 
Объем
шара равен  где R –
радиус шара.
где R –
радиус шара.
Площади поверхности цилиндра, конуса, шара
Пользуясь
формулой объема шара, можно получить
формулу площади поверхности шара, то
есть сферы. Рассмотрим произвольный
многогранник, описанный вокруг сферы,
имеющей радиус R.
Тогда объем многогранника можно найти
по формуле 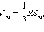 где
где  –
площадь поверхности многогранника.
Будем увеличивать число граней
многогранника так, что площадь каждой
грани неограниченно уменьшается.
Получим, что объем шара выражается
формулой
–
площадь поверхности многогранника.
Будем увеличивать число граней
многогранника так, что площадь каждой
грани неограниченно уменьшается.
Получим, что объем шара выражается
формулой 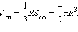 Таким
образом, площадь
сферы выражается
формулой
Таким
образом, площадь
сферы выражается
формулой
|
|
Площадь поверхности цилиндра
|
|
где R – радиус основания цилиндра, H – его высота.
Площадь поверхности конуса
|
|
где R – радиус основания конуса, l – длина его образующей.