Вписанные и описанные многогранники

Определение 5.11. 

Выпуклый многогранник называется вписанным, если все его вершины лежат на некоторой сфере. Эта сфера называется описанной для данного многогранника.

Определение 5.12. 

Выпуклый многогранник называется описанным, если все его грани касаются некоторой сферы. Эта сфера называется вписанной для данного многогранника.

При рассмотрении понятий вписанной и описанной сферы обнаруживается аналогия с понятием вписанной и описанной окружности. Однако, если в любой треугольник можно вписать окружность и около любого треугольника можно описать окружность, то не всякий многогранник является вписанным или описанным. Несмотря на это, оказывается, что пространственный аналог треугольника – треугольная пирамида, тем не менее, всегда имеет единственную вписанную и описанную сферу. Докажем это.

Теорема 5.6. Теорема об описанной сфере треугольной пирамиды.

Треугольная пирамида имеет единственную описанную сферу.

Теорема 5.7. Теорема о вписанной сфере треугольной пирамиды.

Треугольная пирамида имеет единственную вписанную сферу.

Теорема 5.8. 

Для того, чтобы пирамида была вписанной в сферу, необходимо и достаточно, чтобы ее основанием был вписанный в окружность многоугольник.

Следствие 5.9.1. 

Любая правильная пирамида является вписанной.

Теорема 5.9. 

Пусть центр сферы, описанной вокруг пирамиды, лежит на прямой, проходящей через высоту пирамиды. Тогда

1. b² = 2RH,

2. r² = H(2R – H),

где R – радиус описанной сферы, H и b – соответственно высота и боковое ребро пирамиды, а r – радиус окружности, описанной вокруг основания пирамиды.

Теорема 5.10. 

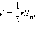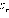Если сфера вписана в многогранник, то объем этого многогранника равен  где  – площадь полной поверхности многогранника, r – радиус вписанной сферы.

Поскольку центр вписанной сферы одинаково удален от всех граней многогранника, он лежит на пересечении биссекторных плоскостей всех двугранных углов многогранника.

Теорема 5.11. 

В правильную n-угольную пирамиду можно вписать сферу.

Определение объема тела

Понятие объема в пространстве вводится аналогично понятию площади для фигур на плоскости.

Определение 6.1. 

Тело называется простым, если его можно разбить на конечное число треугольных пирамид.

В частности, любой выпуклый многогранник является простым телом.

Определение 6.2. 

Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами:

• равные тела имеют равные объемы; при параллельном переносе тела его объем не изменяется;

• если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей;

• за единицу объема принят объем куба, ребро которого равно единице длины;

Определение 6.3. 

Тела с равными объемами называются равновеликими. Из свойства 2 следует, что если тело с объемом V₁ содержится внутри тела с объемом V₂, то V₁ < V₂.

Теорема 6.1. 

Объем прямоугольного параллелепипеда равен произведению его измерений: V = abc.

Теорема 6.2. 

Объем прямой призмы равен произведению площади основания на высоту: V = SH.

Теорема 6.3. 

Объем наклонной призмы равен площади перпендикулярного сечения на боковое ребро: V = S_пс · l.

Теорема 6.4. 

Объем наклонной призмы равен произведению площади основания на высоту: V = S · H.