
- •1. Задачи, приводящие к понятию определенного интеграла. Определение определенного интеграла.
- •2. Теорема существования определенного интеграла. Свойства определенного интеграла.
- •3. Теорема о связи определенного и неопределенного интегралов. Формула Ньютона-Лейбница.
- •4. Замена переменной в ои.
- •5. Интегрирование по частям в ои.
- •6. Несобственные интегралы по бесконечному промежутку интегрирования
- •7. Несобственные интегралы от ф-й, терпящих бесконечный разрыв
- •8. Применение определенных интегралов для выч. Площадей
- •9. Применение определенного интеграла для выч. Длин дуг
- •10. Применение определенного интеграла для выч. Объемов тел
- •11. Задачи приводящие к дифферинциальным уравнениям. Основныепонятия о дифференциальных уравнениях.
- •12. Дифференциальные уравнения первого порядка. Поле направлений. Изоклины. Задача Коши. Теорема Коши.
- •13. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка.
- •14. Линейные дифференциальные уравнения первого порядка и уравнения Бернулли. Общая схема решения дифференциальных уравнений первого порядка.
- •15. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
- •16.Линейные диф.Уравнения высших порядков. Теорема сущ.И единственности. Свойства решений.
- •17.Теорема о структуре общего решения линейного однородного дифференциального уравнения.
- •18. Линейные однородные диф уравнения 2 порядка с постоянным коэффициентом
- •19. Теорема о структуре общего решения линейного неоднородного уравнения
- •20. Нахождение частного решения для линейного диф уравнения 2 порядка с постоянным коэф и спец правой частью
- •24. Знакоположительные ряды. Первый и второй достаточный признаки сходимости рядов
- •25. Знакоположительные ряды. Признак Даламбера и интегральный признак Коши
- •26.Знакочередующиеся ряды.Признак Лейбница.Абсолютно и условно сходящиеся ряды.
- •27.Знакопеременные ряды. Достаточный признак сходимости. Абсолютно и условно сходящиеся ряды.
- •28.Функциональные ряды. Область сходимости ряда, достаточный признак сходимости.
- •29.Степенные ряды. Радиус сходимости степенного ряда
- •31. Ряд Тейлора.
- •32. Разложение основных эл-ных ф-й в ряд Тейлора.
- •33. Применение рядов к приближенным выч.М и решению дифференциальных уравнений.
- •34.Задачи приводящие к понятию двойного интеграла. Двойной интеграл и его выч..
- •35. Тройной интеграл и его выч..
- •36.Криволинейные интегралы первого и второго рода и их выч.
- •37. Основные понятия и определения теории вероятностей. Классическое определение вероятности.
- •38. Сумма событий. Теорема сложения вероятностей.
- •39. Произведение событий. Теорема умножения вероятностей.
- •40. Формула полной вероятности.
- •41. Схема Бернулли. Формула Бернулли.
- •42. Локальная и интегральная теоремы Лапласа. Формула Пуассона.
- •43. Дискретные случайные величины.
- •44. Числовые характеристики дискретных случайных величин.
- •45.Непрерывные случайные величины. Интегральная и дифференциальная ф-и распределения.
- •46.Числовые характеристики непрерывных случайных величин.
- •48. Нормальный з-н распределения.
- •49.Основные понятия математической статистики. Генеральная совокупность и выборка. Вариационный и интервальный статистические ряды. Полигон. Гистограмма. Эмпирическая ф-я распределения.
- •50.Точечные оценки параметров распределения. Их свойства и выч..
- •51. Интервальные оценки параметров распределения. Доверительный интервал для математического ожидания нормального з-на распределения при известном .
- •52.Интервальные оценки параметров распределения. Доверительный интервал для математического ожидания нормального з-на распределения при неизвестном .
- •53. Элементы корреляционного анализа. Двумерная случайная величина. Функциональная и корреляционная зависимость
42. Локальная и интегральная теоремы Лапласа. Формула Пуассона.
Формулой Бернулли удобно пользоваться в тех случ. когда число испыт. малое, но если число испыт. большое, то тогда возвед. в большие степени вызовет большие трудности; в этом случ. прибег. к формулам Лапласа или формуле Пуассона.
ТЕОРЕМА "Локальная теорема Лапласа"
Пусть
в схеме Бернулли число испыт. l(эль)
- велико и вероятность P
не близка к 0 и 1. В этом случ. вероятность
того, что в серии событий (серия из
n-испыт.)
произойдет ровно k-раз.
Вычисл. по формуле. Pn
(k)
=
 где
где
 – диффер. функ-ия Лапласа. Для этой
функ-ии имеется спец. табл. значений.
– диффер. функ-ия Лапласа. Для этой
функ-ии имеется спец. табл. значений.
ПРИМЕР:
Вероятность того что в рыбхозе карпового
пруду, карп будет зеркальный = 0,2. Найти
вероятность того, что среди поставл. в
продажу 400 карпов 80 будет зеркальными.
 P400
(8) =
P400
(8) =
 ;
(0) =
;
(0) =

ТЕОРЕМА "Интегральная теорема Лапласа"
Если
в схеме Бернулли число испыт. велико, а
вероятность не близка к 0 или 1, то
вероятность того, что событие появится
в серии от k1
до k2
раз =
P
(k,
k2)
= (x")
- (x'),
где x'=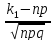 ,
x"=
,
x"=
 ;
(x)
=
;
(x)
=
 dt.
– интегральн. функ-ия Лапласа, для
котор. имеется спец. табл. знач.
dt.
– интегральн. функ-ия Лапласа, для
котор. имеется спец. табл. знач.
ЗАМЕЧАНИЕ ! k1 и k2 могут как входить (включ.) в этот промежуток, так и не вход. (включ.) - роли существ. не играет.
ОТМЕТИМ, что функ-ия (х) - нечетная. (-х) = -(х)
ПРИМЕР:
Вероятность того, что деталь не пройдет
проверку ОТК = 0,2. Найти вероятность
того, чт среди 400 случ. отобр. деталей
проверку ОТК не пройдет от 70 до 100 деталей.
n
= 400, k1
= 70, k2
= 100. P400
(70/100) =
(x")
- (x')
= (2,5)
- (1,25)
= (2,5)
+ (1,25)
= 0, 4938 + 0, 3944 = 0, 8882. x'
=
 .
.
43. Дискретные случайные величины.
Дискретной называют случайную величину которая может принимать только некоторые заранее определенные значения. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счетным мн-вом).
З-н распределения дискретной случ. величины предст. собой перечень всех ее возможных знач. и всех вероятностей. Сумма всех вероятностей pi = 1. з-н распределения может быть так же задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (x0, px).
Биномиальное
распределение.
Биномиальным назыв. з-н распред. дискр.
случ. величины Х - числа появлений события
n-испыт.
независимых, в кажд. из которых вероятность
наступления события постоянна. Вероятности
pi
вычисляют по формуле Бернулли. Для
биномиального распределения: математ.
ожидание М(Х) = np.
дисперсия D(X)
= npq,
коэффиц. асимметрии As
= (q
- p)/ ,
кэффиц. эксцесса Ex
= (1 - pq)/npq.
,
кэффиц. эксцесса Ex
= (1 - pq)/npq.
геометрическое распределение. Производится серия испытаний. Случ. величина - количество испытаний до появл. первого успеха (например, бросание мяча в корзину до первого попадания). Если кол-во испытаний не ограничено, т.е. если случ. величина может принять значен. 1, 2, 3, ..., +, то математ. ожидание и дисперсию геометрич. распредел. можно найти по формулам: М(Х) = 1/р, D(X) = q/p2.
Распределение Пуассона. Пусть имеется некоторая последовательность событий, наступ. в случ-ие моменты времени (будем называть это потоком событий).Интенсивность потока (среднее число событий, появляющихся в единицу времени) равна . Пусть этот поток событий - простейший (пуассоновский) , т.е. обладает тремя свойствами: 1) вероятность появл. k событий за опред. промежуток времени завис. только от длины этого промежутка, но не от точки отсчёта, др. словами, интенсивность потока есть пост. величина (свойство стационарности). 2) вероятность появл. k событ. в любом промеж. времени не завис. от того, появилось событие в прошлом или нет (свойство отсутствия последствия). 3) появление более одного события за малый промежут. времени практически невозможно (свойство ординарности).
