17.Теорема о структуре общего решения линейного однородного дифференциального уравнения.

Если (x), (x), -п-частных линейно независимых решений уравн. Z(y)=0, то его общее решение (с чертой) представляет их линейную комбинацию (с чертой)=C₁y₁(x)+ C₂y₂(x)+…+ C_ny_n(x). C_1,С_2,С_n-const.

18. Линейные однородные диф уравнения 2 порядка с постоянным коэффициентом

Такие уравнения имеют след. Вид: y’’+py’+qy=0 (1), pq-const

Частное решение этого уравнения будем искать в виде: y=l^kx, тогда y’=kl^kx , y’’=k²l^kx

k²l^kx+pkl^kx+ql^kx=0

(k²+pk+q)l^кx=0 , поскольку l^кx≠0, то решение будет тогда, когда ур-ние=0, это ур-ние обращается в 0 только при корнях.

Решим характеристич. уравнения

Возможны след. Случаи: 1. Корни диф уравнения действительные и различные, явл 2-мя линейно-независимыми решениями т.к. ==l^(k1-k2)x ≠const

Общее решение: ȳ=с₁l^k1x+c₂l^k2x

2. корни уравнения действительны и равны между собой

В этом случае: y₁=l_x^k1x y₂=xl^k1x

ȳ= с₁l^k1x+c₂xl^x1=(c₁+c₂x)e^k1x

3. Д<0 ур-ние имеет комплексные корни

К_1,2=α±iᵝ

4. Согласно 4-му свойству решений диф ур-ния решением этого уравнения будут ф-ции y₂=l^αxcosᵝx

y₃=l^αxsinᵝx

эти ф-ции линейно независимы

Общее решение: ȳ=l^αx(l₁cosᵝx+l₂sinᵝx)

Замечание: в частном случае, когда хар-ое ур-ние имеет чисто мнимые корни K_1,2=±ᵝi

ȳ=l₁cosᵝx+l₂sinᵝx

19. Теорема о структуре общего решения линейного неоднородного уравнения

Теорема: общее решение уравнения L(y)=f(x) равно сумме общего решения ȳ однородного уравнения L(y)=0 и любого частного решения y* уравнения у_общ=ȳ+у*

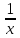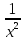y’’+y’+y=x (1)

y₁^k=x y₂= явл частным решением

y’’+y’+y=0

y*=x³ частное решение уравнения 1

тогда ȳ=c₁x+c₂

y_общ=ȳ+y*=c₁x+ c₂+x³

Как найти частное решение: для уравнения 2ого порядка его всегда можно найти методом вариации производ постоянных. Но этот метод сложный поэтому мы рассмотрим метод нахождения частных решений, когда правая часть имеет спец вид

20. Нахождение частного решения для линейного диф уравнения 2 порядка с постоянным коэф и спец правой частью

Такое ур-ние имеет вид: y’’+py’+qy=f(x) (1)

k²+pk+q=0 (2)

f(x)=P_n(n)l^2x P_n(x)=a₀+a₁x+…+a_nxⁿ

Возможны след варианты:

1. K₁≠α, k₂≠α

Α не совпадает ни с одним из корней уравнения. Тогда частное решение y* ищется в виде:

У*=Q_n(x)l^αx

2. K₁=α K₂≠α

y*=xQn(x)l^αx

3. K₁=K₂=α

y*=x²Qn(x)l^2x

В частном случае, когда f(x)=Dn(x), α=0 мы получаем:

k₁, k₂≠0 y*=Qn(x)

k₁=0, k₂≠0 y*=xQn(x)

k₁= k₂=0 y*=x²Qn(x)

Qn(x)- многочлен степени n с производ коэф наход из условия, что у* должно обращаться в тождество (1)

Замечание: этот метод называется методом неопредел коэф., и мы им пользуемся при разложении правильн рацион дробей на простейшие

Вывод: при нахождении частного решения у* мы первоначально записываем у* в таком же виде как у нас есть правая часть, только коэф не определ., затем смотрим совпадают ли корни, характер. ур-ния с корнем правой части. Если нет, то все оставшиеся без изменений . Если да, то домножаем на х в зависимости от количества совпад корней.

№21. Системы дифференциальных уравнений

На практике очень часто встреч процессы, кот описыв системой ДУ, т.е. совокупность ДУ относит нескольких зависимых и одной независ переменной. Простейшей явл линейная сист, кот запис так:

(1) зависим или искоя явл переменная x или y, t явл независ.

Решением этой сист явл совокупность ф-ий x(t) и y(t), кот, будучи подставл в уравн (1) превращ его в тождество. Нач условие для (1):

(2) Точно так же, как и для ДУ, для сист ДУ рассматр общее и частное решение. Общим решением для (1) наз совокупность ф-ий:

Зависим от независим переменн и произв постоянных с₁ и с₂ удовл след 2-м усл:

1. При любых знач произв пост с₁ и с₂ они образ систему в тождество.

2. Для люб нач условий найдутся такие нач произв пост с₁ и с₂, что ф-ии будут явл решением сист удовл задаваем нач усл.

Наиболее распр медоды реш явл метод сведения системы к лин ДУ 2-го порядка.

Пример: Найти общ реш и частное удовл усл:

1. Продиф 1-ое уравн от t 2) Подставл сюда из 2-го уравн: , 3) Из 1-го ур выразим y: (*), 4) Подставим в последнее: 5)

Мы нашли только 1 ф-ию. Ф-ию y(t) найдем из (*), подставим туда x(t) и x^’(t)

№22. Ряды. Основные понятия. Необходимый признак сходимости ряда.

Пусть дана бескон числ послед-ть u₁₁, u₂₁…u_n,…Числ рядом наз выраж:

Ряд наз заданным, если известен будущий член ряда как ф-ия u_n=f(n). Правило, по кот запис члены ряда.

Пример-1.

Пусть задан числ ряд (1). Сумма первых n-членов показыв n-ой численной суммой. S_n=u₁+u₂…+u

Рассмотр последоват-ть частичн сумм: S₁=u_1, S₂=u₁+u_2, S₃=u₁+u₂+u_3, S_n=u₁+u₂+u₃+…+u_n(5),

Если сущ конечный последоват (5) n-ых частичных сумм, то они наз суммой ряда: И ряд назыв сходящ. Если же не сущ или =, то – расходящимся.

Пример-2.

1. Пусть есть ряд (2)

Составим последовательность:

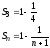
– ряд сходящийся

2. Задан ряд (3)

2+6+18+…+2*3^n-1+…

S₁=2=3-1 S₂=2+6=8=3²-1 S₃=2+6+18=26=3³-1 S_n=3_n-1

–ряд расходится

3. 1-1+1-1+…+(-1)ⁿ⁺¹+…

S₁=1 S₂=0 S₃=1 S₄=0

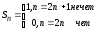
Предел не сущ, т.е. ря расходится.

Рассмотрим в кач-ве примера бесконечн геометр прогрессию.

a+aq+aq²+…+aqⁿ⁺¹+…

Cумма –первых n-слагаемых

1. Если |q|<1, то lim qⁿ=0

2. |q|=1

a+a+a+…+a+… тогда S_n=a*n

–расходится

4. q=-1

a-a+a-a+…+(-1)ⁿ⁺¹a+… (см. ряд (4))

Вывод: геометр прогрессия сходится при |q|<1 и расходится при |q|≥1.

Необходимый признак сходимости ряда

Если числовой ряд (1) сходится, то предел его общего члена =0. Lim u_n=0.

Док-во: поскольку числ ряд сходится, то это знач, что предел посл xck сумм = конечн числу S.

№23. Основные свойства рядов

• Если ряд u₁+u₂+u₃+…+u_n+…(1) сходится, то сходится и ряд: au₁+au₂+…+au_n+… (2) полученный почленным умножением на конечное число S=aS, где S-сумма(1).

• Если сходятся ряды v₁+v₂+…+v_n+…=δ, то сходится и (u₁+u₁)+(u₂+u₂)+…+(u_n+u_n)…=S+δ

• Если сходтся рад u₁+u₂+…+u_k+u_k+1+ u_k+2+…(3), то будет сходится и ряд, полученный отображением первых k-членов u_k+1+ u_k+2+… (2)

И наоборот, если сходится (4), то сходится и (3).

Отбрасывание или добавление конечного числа слагаемых на ходмость ряда не влияет, только влияет на их сумму.