10. Применение определенного интеграла для выч. Объемов тел

Пусть у нас имеется некое тело. Обозначим его за Т. Это тело заключено между 2мя плоскостями x=a, x=b. Обозначаем Vза объем. Дадим приращение dx и найдем насколько прирастем dV. Т.к. приращение dx достаточно малое, то V тела приблизительно равен V цилиндра:

Объем тела вращения: При сечении плоскостью Х=х в сечении получается круг, радиус, равный r=r(x), площадь которого равна , тогда объем тела равен:

11. Задачи приводящие к дифферинциальным уравнениям. Основныепонятия о дифференциальных уравнениях.

Задача о движении парашютиста. Пусть с парашютом сброшен нек. груз Р, нам нужно установить з-н движения парашюта как ф-ю пройденного пути в зависимости от времени.

Мы знаем, что по 2-му з-ну Ньютона f=ma.

С другой стороны, мы знаем, что кроме силы тяжести на парашют действует сила сопротивления воздуха, пропорциональная скорости, и эта сила направлена в противоположную сторону от силы тяжести. dv/dt=mg-kv²

Если мы обозначим через s(t) путь, пройденный парашютом за время е, то v=s’t, a=s’’t.

mg-ks’(t)=ms’’(t)

 s'=s''+k/ms'=g

Таким образом, для нахождения s в зависимости от t мы получим уравения, в кот. входят 1-ая и 2-ая производные искомой ф-и.

ДУ называется ур-ние, связывающее независимую переменную х с искомой ф-ей y и ее производной.

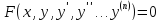
Порядком ДУ называется наивысший из порядков производных, существенно входящих в данное ур-ние.

Решением ДУ явл. ф-я, которая будучи подставленной в ур-ние, обращает его в тождество.

При нахождении решения ДУ приходится прибегать к операции интегрирования, поэтому решением ДУ называют интегрирование ДУ, а график решения ДУ - интегральной кривой. Если решение ДУ сущ., то их будет бесч. мн-во, а самому основному уравнению соответствует целое семейство интегральных кривых.

12. Дифференциальные уравнения первого порядка. Поле направлений. Изоклины. Задача Коши. Теорема Коши.

ДУ первого порядка . Если этого уравнения можно разрешить относительно производной, то оно имеет вид y’=f(x, y).

Мы знаем, что на плоскости данному ур-нию соответствует семейство интегральных кривых. Возьмем одну из кривых, которой соответствует решение y=Y(x). Мы знаем из геом. смысла производной, что она равна тангенсу угла наклона касательной, проведенной к точке. f(x,y)=y’=tgα, поэтому используя ур-ние к плоскости проведем мн-во отрезков с угловым коэффициентом равным правой части. Такое мн-во наз. полем направлений. Геометрически решить ДУ означает провести инт. кривую так, чтобы в каждой точке она совпала с полем напр. Для того чтобы строить поле направлений пользуются изоклинами. Изоклина – мн-во точек плоскости, где поле направлений имеет одно и то же напр. Мн-во этих точек задает кривую. Поле напр. определяет инт. кривые- концентрические окружности с центром в начале координат.

ДУ соответствует бесчисленное мн-во инт. кривых и решений. Для выделения конкретной инт. кривой можно задать точку, через которую она проходит. Решение ДУ при x = x₀ должно удовл. усл y=(x0)=y0, y’|x=x0 = y0, y’’|x=x0 = y’0 (3) - начальное усл. Коши. Задача, состоящая в нахождения решения ур-ния (2) удовл. начальному условию (3) наз. задача Коши для ДУ.

Теорема Коши. Если правая часть ур-ния y’=f(x, y) и ее частная производная f’_y(x,y) непр. в некоторой области G, то для любой точки m₀, принадлежащей этой области, ур-ние имеет решение, удовл. условию y’|x=x₀ = φ(x₀) = y₀

Геом. смысл состоит в том, что через каждую точку области мы можем провести единственную инт. кривую. Точки области, в которых нарушается единственность решения наз. особыми точками области.

Общее и частное решение ДУ первого порядка. Рассмотрим ДУ первого порядка, правая часть которого удовл. условиям теоремы Коши. Функция, зав. от аргумента и произ. постоянной наз. ОР области G, если она удовл. : 1) она обращает в тождество ур-ние (1) при любых значениях произв. постоянной C. 2) для любых начальных условий найдено найдется такое значение C₀, что y=y(x, c₀) будет явл. решением данного ур-ния, удовлетв. заданному начальному условию. Значение произвольной постоянной с0 мы можем найти φ=(x₀,c₀)=y_0. Всякое решение y0= φ(x, c0), полученное из общего решения, называется частным. Часто частное решение получается в неявном виде φ=(x, y, c)=y0 и наз. общим интегралом, φ=(x, y, c0)=y0 - частным интегралом.