Лекция №7 предел функции

4.1. Определения предела функции в точке.Теорема об эквивалентности определений. Односторонние пределы.

Впервые определение предела функции было дано О. Коши в 1821 г.

Пусть функция определена на некотором множестве . Рассмотрим последовательность точек , сходящуюся к точке , при этом может и не принадлежать множеству . Соответствующие значения функции в точках этой последовательности также образуют числовую последовательность .

Определение 1 (по Гейне). Число называется пределом функции в точке (при ), пишут , если для любой сходящейся к последовательности значений аргумента , отличных от , соответствующая последовательность значений функции сходится к числу .

Функция может иметь в точке только один предел, так как последовательность имеет только один предел.

Определение 2 (по Коши). Число называется пределом функции в точке (при ), пишут , если для любого числа существует такое число , что для всех (), удовлетворяющих неравенству , выполняется .

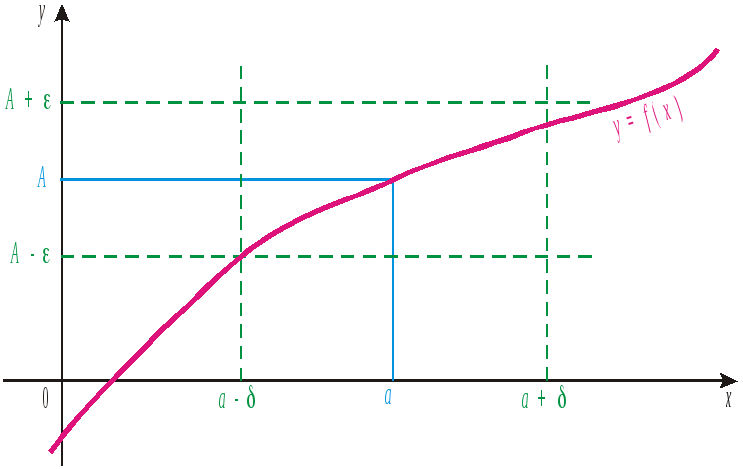
Рис. 1

Определение 3 (геометрическое определение предела функции). Число называется пределом функции , если для любой окрестности точки найдется такая окрестность точки , что для всех из этой окрестности соответствующие значения функции лежат в окрестности точки , т.е. точки графика функции лежат внутри полосы шириной , ограниченной прямыми , . Очевидно, что величина зависит от выбора (рис. 1).

Пример 1. Доказать, что .

Решение. Воспользуемся неравенством . Зададим произвольное и положим . Тогда, если , то . Это и означает (согласно определению предела функции по Коши), что .

Теорема 1. Определения предела функции по Коши и по Гейне эквивалентны.

Доказательство. Пусть b является пределом функции в точке а по Коши. Докажем, что это же число является пределом функции в точке а по Гейне. Пусть – любая сходящаяся к а последовательность значений аргумента, все элементы которой отличны от а. Требуется доказать, что соответствующая последовательность значений функции сходится к b.

Фиксируем произвольное положительное число ε и по нему положительное число δ, которое в силу определения предела функции по Коши гарантирует справедливость неравенства для всех значений х, для которых 0<|x–a|<δ. В силу сходимости последовательности к а для указанного числа δ найдётся такой номер N, что при всех nN справедливо неравенство . Поскольку для всех номеров n, то при всех справедливы неравенства 0< и, значит, в силу определения предела функции по Коши , но это и означает сходимость последовательности к числу b.

Пусть теперь число b является пределом функции в точке а по Гейне. Докажем, что это же число является пределом функции в точке а по Коши. Предположим, что это не так. Тогда для некоторого положительного числа ε и для любого сколь угодно малого положительного числа δ найдётся хотя бы одно значение аргумента х, такое, что , но . Таким образом, мы можем взять последовательность с натуральными n и утверждать, что для каждого ее элемента найдется хотя бы одно значение аргумента x_n такое, что , но . Левое из неравенств означает, что последовательность {x_n} сходится к числу а и состоит из чисел, отличных от а. Но в таком случае согласно определению предела по Гейне соответствующая последовательность значений функции обязана сходится к b, а этому противоречит правое из неравенств, справедливое для всех номеров n. Полученное противоречие доказывает теорему.

Пример 2. Доказать, что функция не имеет предела при .

Решение. Докажем, что эта функция не удовлетворяет определению предела функции при по Гейне. Для этого укажем такую бесконечно большую последовательность , что последовательность расходится. Положим . Тогда , а последовательность расходится. Отсюда следует, что функция не имеет предела при .

В определении предела функции считается, что стремится к любым способом, оставаясь меньше или больше, чем . Если способ приближения аргумента к существенно влияет на значение предела, то рассматриваются односторонние пределы.

Определение 4. Число называется правым (левым) пределом функции в точке при , пишут (), если для любого числа существует такое число , что для всех , удовлетворяющих неравенству (), выполняется неравенство .

Теорема 2. Для того, чтобы функция имела в точке предел, необходимо и достаточно, чтобы в этой точке существовали левый и правый пределы и чтобы они были равны. В этом случае предел функции равен односторонним пределам

.

Доказательство. В самом деле, пусть . Тогда, согласно определению предела функции в точке a, это означает, что для любого числа ε>0 существует такое число δ>0, что для всех точек x, удовлетворяющих условию , , выполняется неравенство . Тем самым, как для точек x, таких, что , так и для таких, что , справедливо неравенство . А это, согласно определению и означает, что число А является как пределом функции справа, так и пределом функции слева: .

Обратно, пусть существуют оба предела и они равны. Согласно определению для всякого ε>0 существуют такие и , что для всех х, удовлетворяющих условию и для всех х, удовлетворяющих условию справедливо неравенство. Если обозначить через δ наибольшее из чисел δ₁ и δ₂, то очевидно, что для всех х, удовлетворяющих условию , , будет справедливо неравенство . Это и означает, что .

Пример 3. Пусть

и не определена при . Существует ли ?

Решение. Вычислим в точке односторонние пределы функции

;

.

Отсюда по теореме 2 следует, что существует и равен нулю.

Дадим определение предела функции при стремлении аргумента к бесконечности.

Определение 5. Число называется пределом функции при , пишут , если для любого числа существует такое число N, что для всех (), удовлетворяющих неравенству , выполняется .

Определение предела функции при графически иллюстрируется следующим образом:

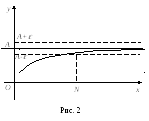
Для любой сколь угодно малой -окрестности около ординаты найдется такое значение , что для всех  график функции не будет выходить за пределы полосы шириной 2.