
1.6. Ограниченные числовые множества.Точные грани числовых множеств
Определение
1. Числовое множество
![]() называется ограниченным
сверху (снизу),
если существует число
называется ограниченным
сверху (снизу),
если существует число
![]() (
(![]() )
такое, что для всех
)
такое, что для всех
![]() выполняется неравенство
выполняется неравенство
![]() (
(![]() ).
).
Определение 2. Числовое множество, которое ограничено и сверху и снизу, называется ограниченным. Примерами ограниченных числовых множеств являются отрезок, интервал, полуоткрытый промежуток.
Число
![]() (
(![]() )
называется верхней
(нижней)
границей
множества
)
называется верхней
(нижней)
границей
множества
![]() .
.
Определение
3. Наименьшая из верхних
границ непустого ограниченного сверху
множества
![]() называется точной
верхней гранью этого
множества и обозначается
называется точной
верхней гранью этого
множества и обозначается
![]()
![]() (supremum).
(supremum).
Теорема 1. Непустое множество, ограниченное сверху, имеет точную верхнюю грань, притом единственную.
Теорема
2. Для того чтобы число
![]() было точной верхней гранью непустого
числового множества
было точной верхней гранью непустого
числового множества
![]() ,
необходимо и достаточно, чтобы:
,
необходимо и достаточно, чтобы:
1)
для всех
![]() выполнялось неравенство
выполнялось неравенство
![]() ;
;
2)
для любого действительного числа
![]() нашлось такое
нашлось такое
![]() ,
что
,
что
![]() .
.
Определение
4. Наибольшая из нижних
границ непустого ограниченного снизу
множества
![]() называется точной нижней
гранью этого множества
и обозначается
называется точной нижней
гранью этого множества
и обозначается
![]()
![]() (infimum).
(infimum).
Теорема 3. Непустое множество, ограниченное снизу, имеет точную нижнюю грань, притом единственную.
Теорема
4. Для того чтобы число
![]() было точной нижней гранью непустого
числового множества
было точной нижней гранью непустого
числового множества
![]() ,
необходимо и достаточно, чтобы:
,
необходимо и достаточно, чтобы:
1)
для всех
![]() выполнялось неравенство
выполнялось неравенство
![]() ;
;
2)
для любого действительного числа
![]() нашлось такое
нашлось такое
![]() ,
что
,
что
![]() .
.
Пример
1. Пусть
![]() ,
,
![]() и
и
![]() ,
тогда
,
тогда
![]() и
и
![]() .
.
Этот пример показывает, в частности, что нижняя и верхняя грани могут как принадлежать, так и не принадлежать самому множеству.
Пример
2. Пусть
![]() .
Докажем, что
.
Докажем, что
![]() ,
,
![]() .
.
Решение.
Для любого натурального
числа
![]() имеем
имеем
![]() ,
а потому 1 – одна из верхних граней для
,
а потому 1 – одна из верхних граней для
![]() .
Предположим теперь, что
.
Предположим теперь, что
![]() .
Тогда найдется такое
.
Тогда найдется такое
![]() ,
что
,
что
![]() .
С другой стороны,
.
С другой стороны,
![]() ,
а потому при
,
а потому при
![]() имеем
имеем
![]() .
Из этого неравенства следует, что
.
Из этого неравенства следует, что
![]() .
Мы нашли, таким образом, элемент
.
Мы нашли, таким образом, элемент
![]() ,
такой, что
,
такой, что
![]() .
Итак, для множества
.
Итак, для множества
![]() и числа 1 выполнены оба сформулированных
выше утверждения, и потому
и числа 1 выполнены оба сформулированных
выше утверждения, и потому
![]() .
Само число 1 не принадлежит
.
Само число 1 не принадлежит
![]() .
.
Далее,
имеем
![]() .
Отсюда видно, что при увеличении
.
Отсюда видно, что при увеличении
![]() разность
разность
![]() увеличивается. Значит, наименьшее
значение разности достигается при
увеличивается. Значит, наименьшее
значение разности достигается при
![]() ,
и это значение равно
,
и это значение равно
![]() .
Таким образом,
.
Таким образом,
![]() – наименьший элемент множества
– наименьший элемент множества
![]() ,
а потому
,
а потому
![]() .
.
1.7. Классификация точек множества. Теорема Больцано-Вейерштрасса
Определение
1. Для любого
![]()
![]() -окрестностью
точки
-окрестностью
точки
![]() называется множество
называется множество
![]() .
.
В
случае
![]()
![]() ,
а в случае
,
а в случае
![]()
![]() .
.
Определение
2. Проколотой
![]() -окрестностью
точки
-окрестностью
точки
![]() называется множество, получающееся
удалением точки
называется множество, получающееся
удалением точки
![]() из ее
из ее
![]() -окрестности:
-окрестности:
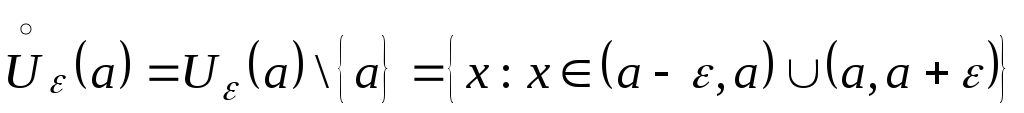 .
.
Определение
3. Точка
![]() называется внутренней
точкой множества
называется внутренней
точкой множества
![]() ,
если существует
,
если существует
![]() -окрестность
-окрестность
![]() ,
целиком принадлежащая
,
целиком принадлежащая
![]() .
.
Определение
4. Точка
![]() называется граничной
точкой множества
называется граничной
точкой множества
![]() ,
если в каждой ее окрестности существуют
точки как принадлежащие множеству
,
если в каждой ее окрестности существуют
точки как принадлежащие множеству
![]() ,
так и не принадлежащие множеству
,
так и не принадлежащие множеству
![]() .
.
Определение
5. Точка
![]() называется точкой
прикосновения множества
называется точкой
прикосновения множества
![]() ,
если в каждой ее окрестности существует
хотя бы одна точка, принадлежащая
множеству
,
если в каждой ее окрестности существует
хотя бы одна точка, принадлежащая
множеству
![]() .
.
Если
точка прикосновения является одной из
бесконечностей:
![]() ,
,
![]() или
или
![]() ,
то она называется бесконечно
удаленной точкой прикосновения.
,
то она называется бесконечно
удаленной точкой прикосновения.
Очевидно,
что все элементы числового множества
являются его точками прикосновения.
Точками самого множества не исчерпываются,
вообще говоря, все его точки прикосновения:
могут существовать точки прикосновения
и не принадлежащие ему. Например, точки
![]() и
и
![]() являются точками прикосновения интервала
являются точками прикосновения интервала
![]() и не содержатся в нем.
и не содержатся в нем.
Определение
6. Точка
![]() называется предельной
точкой множества
называется предельной
точкой множества
![]() ,
если в каждой ее проколотой окрестности
существует хотя бы одна точка, принадлежащая
множеству
,
если в каждой ее проколотой окрестности
существует хотя бы одна точка, принадлежащая
множеству
![]() .
.
Предельная точка всегда является точкой прикосновения, но не наоборот. Для множества рациональных чисел предельной является каждая точка R, так как в любом интервале вещественных чисел имеются рациональные числа.
Определение
7. Точка
![]() называется изолированной
точкой
множества
называется изолированной
точкой
множества
![]() ,
если у нее существует окрестность, не
содержащая других точек множества
,
если у нее существует окрестность, не
содержащая других точек множества
![]() ,
кроме самой точки
,
кроме самой точки
![]() .
.
Пример.
Рассмотрим множество
![]() .
Для этого множества:
.
Для этого множества:
0, 1, 5 – граничные точки;
![]() и
и
![]() – точки прикосновения;
– точки прикосновения;
![]() – предельные точки;
– предельные точки;
5 – изолированная точка.
Определение 8. Множество, содержащее все свои предельные точки, называется замкнутым.
Определение 9. Множество, у которого все точки являются внутренними, называется открытым.
Определение
10. Совокупность всех
точек прикосновения множества
![]() называется его замыканием
называется его замыканием
![]() .
.
Определение 11. Ограниченное замкнутое множество называется компактом.
Теорема (Больцано-Вейерштрасса). Всякое бесконечное ограниченное числовой множество имеет хотя бы одну предельную точку.
Доказательство. Пусть А – ограниченное множество, тогда существует такой отрезок [c, d], которому принадлежит А. Так как А – бесконечное множество, то хотя бы на одной из двух половин [c, (c+d)/2], [(c+d)/2, d] отрезка [c, d] имеется бесконечное подмножество множества А. Пользуясь этим очевидным предположением, отправляясь от отрезка [c, d] =∆1 с заданным на нем бесконечным множеством точек А, построим систему вложенных отрезков ∆n, где каждый последующий отрезок составляет половину предыдущего и несет на себе бесконечное подмножество множества А. По принципу Кантора у этой системы есть общая точка х0, докажем, что она является предельной для множества А. Возьмём любой интервал V с центром в точке х0 ,скажем, длины σ>0. Пусть n таково, что длины отрезка ∆n меньше σ/2. Включая в себя точку х0, он целиком содержится в интервале V. Вместе с отрезком ∆n в интервал V попадет бесконечное число точек множества А. Следовательно, х0 есть предельная точка множества А, что и требовалось доказать.
Эта теорема также выражает принцип полноты числовой прямой, как и леммы Коши-Кантора и Бореля-Лебега.
