Передаточная функция

В теории автоматического регулирования часто используют уравнение не для самих переменных, а для их изображений (других переменных), получаемых с помощью преобразования Лапласа.

Изображения для входных и выходных сигналов находится путем замены переменной t на комплексную переменную p по формуле:

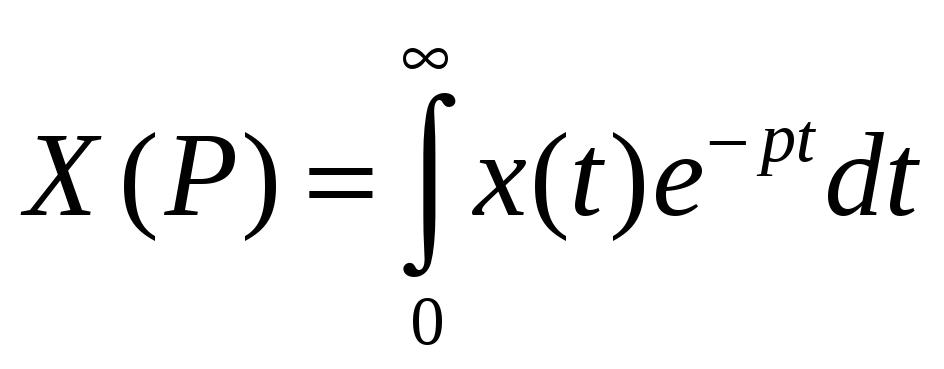; . (2.7)

где x(t), y(t) - входная и выходная величины;

X(t), Y(t) - изображение входной и выходной величин;

p - оператор Лапласа.

В результате использования преобразования Лапласа операция дифференцирования и интегрирования переменных x и у становится эквивалентной умножению и делению изображений этих переменных на р:

, , . (2.8)

Это в конечном итоге позволяет любое интегро-дифференциальное уравнение свести к алгебраическому. Так из уравнения (2.1) путем преобразования Лапласа получается алгебраическое уравнение в виде:

(2.9)

Из этого уравнения можно получить простой вид связи между изображениями входной и выходной величин:

(2.10)

или иначе:

. (2.11) (2.3)

Для формального перехода от уравнения (2.1) к уравнению (2.9) следует заменить x(t) на Х(р) и у(t) на Y(р), на p и на p².

Функция W(р), связывающая изображение выходного сигнала с изображением входного, называется передаточной функцией.

Итак, общий вид передаточной функции для типового динамического звена имеет вид:

. (2.12) (2.4)

Из выражения (9) и (10) получим:

; . (2.13)

Передаточная функция представляет собой оператор, который, будучи приложенным к изображению входной величины, дает изображение выходной.

Существует непосредственная связь между передаточной функцией и уравнением и простой переход от одного к другому. Передаточная функция, таким образом, является более удобной формой изображения дифференциального уравнения и так же полностью описывает свойство элемента или всей системы.

Выполнив формально преобразования Лапласа для уравнений типовых динамических звеньев (2.2-2.6) нетрудно получить для них соответствующие передаточные функции:

Пропорциональное звено W(p) = К.

Апериодическое звено .

Дифференцирующее звено .

Интегрирующее звено .

Колебательное звено .

Использование передаточных функций позволяет по известным свойствам элементов системы регулирования определить передаточную функцию системы вцелом и из нее получить уравнение, определяющее все ее свойства (устойчивость, качество регулирования, предельные эксплуатационные параметры и т.п.).

Преобразование структурных схем систем автоматического регулирования

Уравнение САР связывает входной (задающий) сигнал с выходным сигналом, например, значением регулируемого параметра.

Определение уравнения осуществляется путем преобразования структурной схемы, которое заключается в последовательной замене нескольких соединенных между собой звеньев на одно эквивалентное с эквивалентной передаточной функцией. Такая последовательная замена звеньев эквивалентными позволяет получить общую передаточную функцию автоматической системы. Затем из передаточной функции путем обратного преобразования Лапласа находят дифференциальное уравнение системы.

Типовые динамические звенья в структурной схеме автоматической системы могут соединяться между собой тремя способами: последовательно, параллельно и с обратной связью. Определим эквивалентную передаточную функцию для каждого вида соединений.

Последовательное соединение типовых динамических звеньев (рис. 2.2) характеризуется последовательным прохождением сигнала через каждое звено. Для определения эквивалентной передаточной функции W(P) необходимо найти связь между выходным сигналом Y и входным X.

Pиc. 2.2 Последовательное соединение звеньев

Поскольку ; ; .

.

Поэтому , (2.13)

Итак, передаточная функция последовательно соединенных звеньев равна произведению их передаточных функции.

Параллельное соединение звеньев показано на рис. 2.3. При этом соединении входной сигнал X поступает на вход каждого звена, а выходные сигналы от звеньев, суммируясь, формируют выходной сигнал Y. Y=y₁+y₂+y₃.

Поскольку y₁=W₁(P)Х; y₂=W₂(P)Х; y₃=W₃(P)Х;

то Y= W₁(P)Х+ W₂(P)Х+ W₃(P)Х=[W₁(P)+W₂(P)+W₃(P)]Х.

Учитывая, что Y= W(P)Х, поэтому

W(P) = W₁(P)+W₂(P)+W₃(P). (2.14)

Рис.2.3 Параллельное соединение звеньев

Итак, передаточная функция параллельно соединенных звеньев равна сумме их передаточных функций.

Соединение с обратной связью показано на рис. 2.4. Выходной сигнал Y звена с передаточной функцией W₁(P) по цепи обратной связи проходит через звено с передаточной функцией W₂(P) и складывается или вычитается с входным сигналом X, а результат является входным сигналом для звена W₁(P). Если ε = Х + Y, то обратная связь называется положительной, если ε = Х - Y, то обратная связь называется отрицательной. Изображение на структурной схеме отрицательной обратной связи показано на рис.2.4.

Рис.2.4 Соединение с обратной связью:

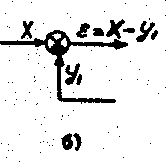
Для случая отрицательной обратной связи, обычно используемой в автоматике, можно найти эквивалентную передаточную функцию следующим образом:

, (2.15)

, (2.16)

Подставляя выражение (2.15) в (2.16), найдем связь между Y и X .

(2.17)

откуда находим, что передаточная функция звена, охваченного отрицательной обратной связью, равна:

, (2.18)

Аналогично можно найти передаточную функцию эвена, охваченного положительной обратной связью, которая имеет вид:

, (2.19)

Пример. Найдем дифференциальное уравнение системы автоматического регулирования температуры по заданной структурной схеме, приведенной на рис.2.4.

к₁=100, к₂=10, Т=0,5; к₃=1

Рис. 2.4 Структурная схема САР

В данной структурной схеме имеется два последовательно соединенных звена (пропорциональное и апериодическое), охваченные отрицательной обратной связью, в цепи которой стоит пропорциональное звено. В соответствии с уравнением 1 найдем передаточную функцию последовательно соединенных звеньев.

(2.20)

Затем по формуле (2.19) имеем:

(2.21)

Умножая в знаменателе скобку на скобку, получаем:

(2.22)

Подставим численные значения коэффициентов:

(2.23)

Дифференциальное уравнение находится из передаточной функции следующим образом. Учитывая, что передаточная функция связывает изображения входного и выходного сигнала, запишем:

или ; (2.24)

Освободимся от знаменателя и одновременно используем выражение:

, и получим дифференциальное уравнение для рассмотренной автоматической системы в виде:

(2.25)

Лекция 3

Устойчивость автоматических систем