Министерство образования Российской федерации
Петрозаводский государственный университет
Кольский филиал
«ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ»
Учебно-методическое пособие
Апатиты
2003
УДК 517.9
Обыкновенные дифференциальные уравнения высших порядков. /Учебно-методическое пособие для решения задач. //составил к.т.н. - Терещенко С.В./ –Апатиты.: Издание КФ ПетрГУ., 2003. –107 с.
Пособие охватывает такие следующие разделы темы: виды интегрируемых нелинейных уравнений п-го порядка; уравнения п-го порядка, допускающие понижения порядка; линейные уравнения высших порядков с постоянными и переменными коэффициентами; краевые задачи для уравнений п-го порядка.
В каждом параграфе приводятся необходимые теоретические сведения. Типовые задачи даются с подробными решениями. Имеются задачи для самостоятельной работы с ответами. Варианты контрольных работ, содержащиеся в пособии, могут быть использованы как для работы со студентами очного, так и заочного отделения.
Рецензенты:
кафедра высшей математики филиала Санкт-Петербургского инженерно-экономического университета в г. Апатиты, заведующий кафедрой высшей математики филиала, доктор физико-математических наук Мингалев В.С.;
кафедра информационных систем Кольского филиала Петрозаводского государственного университета, профессор, доктор технических наук Богатиков В.Н.
Печатается по решению редакционно-издательского совета Петрозаводского государственного университета в качестве учебно-методического пособия
© Издательство Петрозаводского
Государственного университета
Кольский филиал,2002
СОДЕРЖАНИЕ
1. Основные понятия 5
2. Виды интегрируемых нелинейных уравнений п-го порядка 6
2.1. Дифференциальное уравнение вида 6
2.2. Дифференциальное уравнение вида 11
2.3. Дифференциальные уравнения вида 13
2.4. Уравнения, левая часть которого есть точная производная 15
Задания для самостоятельной работы 19
3. Уравнения п-го порядка, допускающие понижения порядка. 19
3.1. Уравнения вида 19
3.2. Уравнение вида 20
3.3. Уравнение, однородное относительно искомой функции и ее производных 22
3.4. Обобщенно однородное дифференциальное уравнение вида 23
3.5. Уравнения, приводимые к виду 26
Задания для самостоятельной работы 27
4. Линейные уравнения высших порядков 28
4.1. Введение 28
4.1.1. Однородное уравнение 28
4.1.2. Неоднородное линейное уравнение 33
4.2. Линейные дифференциальные уравнения с постоянными коэффициентами 37
4.2.1. Однородное уравнение 37
4.2.2. Неоднородные линейные уравнения 42
Задания для самостоятельной работы 64
4.3. Линейные дифференциальные уравнения с переменными коэффициентами 66
4.3.1. Уравнения Эйлера 66
Задания для самостоятельной работы 71
4.4. Дифференциальные уравнения второго порядка 72
4.4.1. Приведение уравнения 2-го порядка к каноническому виду 72
4.4.2. Метод исключения из уравнения 2-го порядка слагаемого, содержащего первую производную искомой функции. Уравнение Чебышева 73
Задания для самостоятельной работы 75
4.4.3. Приведение уравнения 2-го порядка к самосопряженному виду 75
4.4.4. Краевая задача для уравнения 2-го порядка 77
Задачи для самостоятельной работы 84
4.4.5.Решение уравнений второго порядка с помощью рядов 84
Задачи для самостоятельной работы 95
4.4.6.Метод малого параметра. 96
Задания для самостоятельной работы 100
Контрольные работы 101
Ответы к заданиям для самостоятельной работы 103
Список использованных источников 110
1. Основные понятия
Дифференциальным уравнением n-го порядка называется уравнение вида:
.
(1)
Если это уравнение является уравнением, разрешенным относительно старшей производной, то может быть записано в виде:
(2)
Функция
называется
решением (1) или (2) в некотором интервале
[a,b],
если для всех значений х
из этого интервала выполняется тождество:
,
(3)
или
(4)
При этом
предполагается, что функция
имеет непрерывные производные до n-го
порядка включительно и что точка [
]
принадлежит области определения
функции
;
если речь идет об уравнении (2), то точка
принадлежит области определения функции
.
График решения
есть
интегральная кривая.
Задача Коши для уравнения n-го порядка состоит в том, чтобы найти решение уравнения, удовлетворяющее условиям:
при
,
(5)
где
- заданные числа, которые называются
начальными данными, или начальными
условиями.
Функция
называется общим решением уравнения
n-го
порядка, если при соответствующем выборе
произвольных постоянных С1,
С2,
С3,…,
Сn
эта функция является решением любой
задачи Коши, поставленной для данного
уравнения. Всякое решение, получаемое
из общего решения при конкретных
значениях постоянных С1,
С2,
С3,…,
Сn
, называется частным решением этого
уравнения.
Во многих случаях, интегрируя уравнение (2), получают соотношение вида:
(6)
Такое соотношение называется промежуточным интегралом k-го порядка уравнения (2).
Промежуточный интеграл вида:
(7)
называется первым интегралом.
Зная k независимых первых интегралов, можно понизить порядок уравнения на k единиц. Знание п независимых первых интегралов дает возможность путем исключения производных получить общий интеграл.
Интегрирование дифференциальных уравнений n-го порядка (в конечном виде) удается произвести только в некоторых случаях, которые мы далее рассмотрим.
2. Виды интегрируемых нелинейных уравнений п-го порядка
2.1. Дифференциальное уравнение вида
Дифференциальное
уравнение вида
может быть проинтегрировано, если
уравнение
можно разрешить или относительно
или же относительно
.
Действительно, в первом случае имеем
,
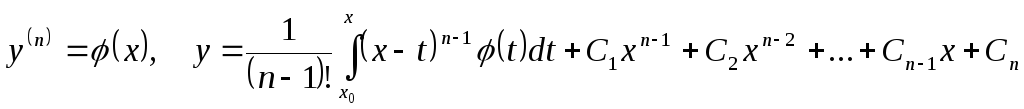(8)
где Cj
(
)
– произвольные постоянные.
Во втором случае
полагаем
.
Тогда
и
,
откуда
.
Аналогично находятся
,
где g и - известные функции.
Таким образом,
общее решение уравнения
находится в параметрической форме, а
именно:
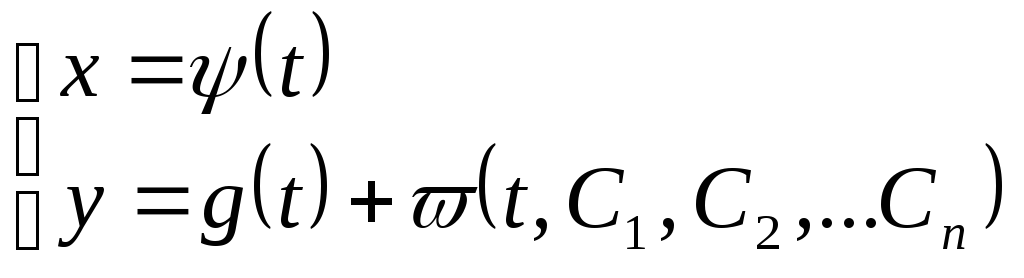(9)
Иногда уравнению
удовлетворяют параметрические уравнения:
,
т.е.
при t(t0,t1).
Тогда, действуя аналогично изложенному
выше, получаем параметрические уравнения
общего решения, имеющего вид (9).
Пример 1.
Найти общее решение уравнения:
и выделить решение, удовлетворяющее
начальным условиям:
при х = 0.
▲ Интегрируя последовательно исходное уравнение, получим
Найдем решения,
удовлетворяющие начальным условиям.
Подставим начальные данные
в полученную систему:
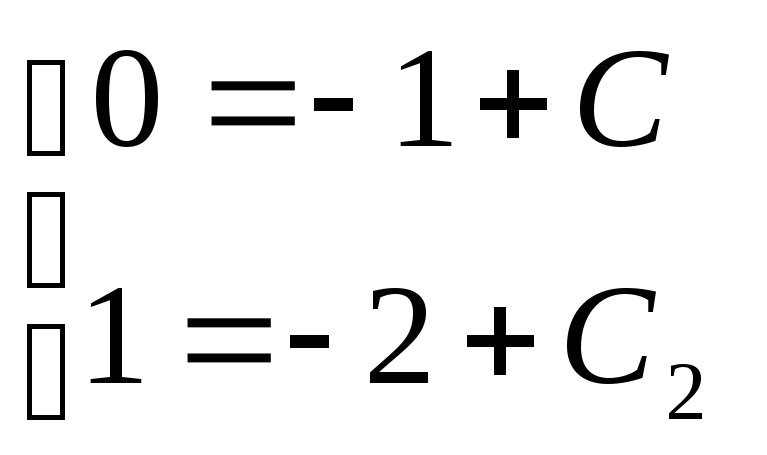
откуда найдем С1 = 1 и С2 = 3. Поэтому искомое решение будет иметь вид:
.▲
Пример 2.
Найти общее решение уравнения:
.
▲Так как интеграл от правой части не выражается в элементарных функциях, то вместо последовательного интегрирования можно воспользоваться формулой (8). Полагая в ней п = 2 и х0 = 0, получаем
.▲
Пример 3.
Найти общий интеграл уравнения:
.
▲ Это уравнение
разрешается относительно
:
и
.
Интегрируя эти уравнения, получим:
и
Совокупность этих общих решений образует общий интеграл исходного уравнения. Его можно записать в виде:
.▲
Пример 4.
Найти решения уравнения:
.
▲ Это уравнение
разрешается относительно
:
и
.
Для решения этих
уравнений введем параметр t,
положив, например,
.
Тогда получим:
и
.
Решим первое из этих двух уравнений. Используем равенства
,
а dx найдем из
,а
именно
,
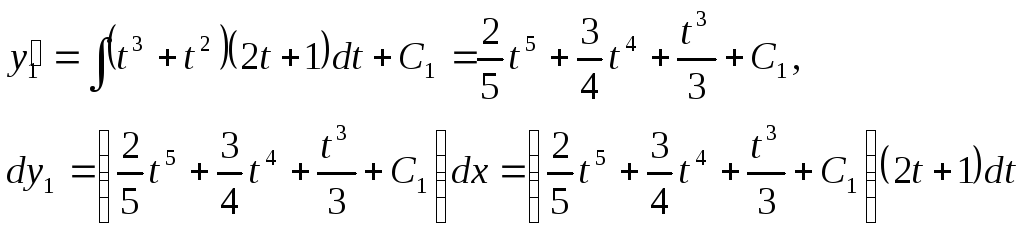
Интегрируя последнее выражение, находим:
.
Для того, чтобы найти у2 необходимо поступить аналогичным образом:
.▲
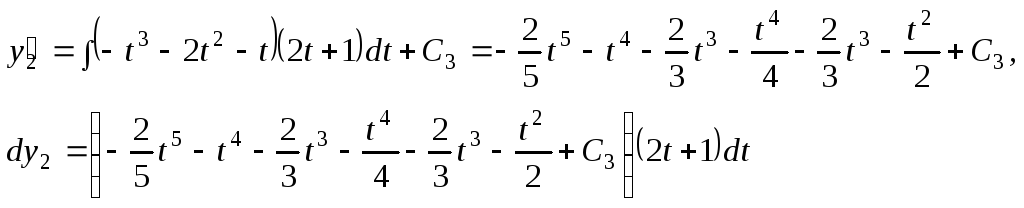
Пример 5. Найти решения уравнения:
.
▲ Это уравнение
неразрешимо относительно
.
Однако оно разрешимо относительно х:
и поэтому, если
принять
за t, то получим
параметрическое представление исходного
уравнения:
Из этого уравнения найдем выражение для dx:
,
которое, вместе с
подстановкой,
,
подставим в известное выражение:
,
а именно:
.
Далее из выражения
,
находим:
.▲
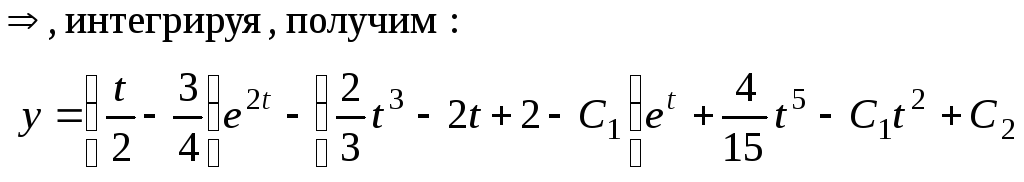Пример 6. Найти общее решение уравнения:
.
▲ Это уравнение
разрешимо относительно
:
.
Для решения этого
уравнения введем параметр t
по формуле
.
Тогда предыдущее уравнение можно
представить в виде:
.
Так как
,
то в силу параметрических представлений
производных
получим
уравнение:
,
интегрирование которого дает
.
Функцию у
найдем из уравнения
,
или
,
пользуясь предыдущим уравнением для
нахождения dx:
.
Таким образом, общее решение исходного уравнения имеет вид:
.▲