4.4.4. Краевая задача для уравнения 2-го порядка

Наряду с задачей Коши, являющейся основной задачей теории дифференциальных уравнений, большое значение имеет задача, в которой, в отличие от задачи Коши, дополнительные условия задаются не в одной точке, а на концах некоторого промежутка [a,b], внутри которого ищется решение. Такие условия называются граничными или краевыми, а сама задача нахождения решения уравнения, удовлетворяющего краевым условиям, называется краевой задачей.

Пример 46. Найти решение уравнения: , удовлетворяющее условиям: .

▲ Поскольку это однородное линейное уравнение с постоянными коэффициентами, то для него можно записать характеристическое уравнение , корни которого и определяют его общее решение:

.

Первое граничное условие удовлетворяется при , при этом .

Если , где n – целое число, то из второго граничного условия находим

.

Таким образом, в этом случае существует единственное решение краевой задачи

.

Если же и , то все кривые пучка являются графиками решений краевой задачи.

При и решений краевой задачи не существует, так как ни одна кривая пучка не проходит через точку , где , .▲

Рассмотрим вопрос о решении простейшей краевой задачи для линейного уравнения 2-го порядка (84)

. (91)

где и требуется найти решение этого уравнения, удовлетворяющее краевым условиям

(92)

Сделаем стандартизацию краевой задачи (91), (92), преобразовав уравнение (91) и краевые условия (92) к специальному виду.

Преобразуем уравнение (91), приведя соответствующее однородное уравнение к самосопряженному виду

(93)

Для этого умножим обе части уравнения (91) на функцию . В итоге получим

или

так что

>0, .

Заменим краевые условия (92) нулевыми краевыми условиями. Для этого сделаем замену искомой функции у по формуле

.

Получим

.

Таким образом, не умаляя общности, достаточно найти решение краевой задачи в стандартной форме

(94)

С этой целью введем в рассмотрение функцию , удовлетворяющую следующим условиям:

1. непрерывна по х при фиксированном s при .

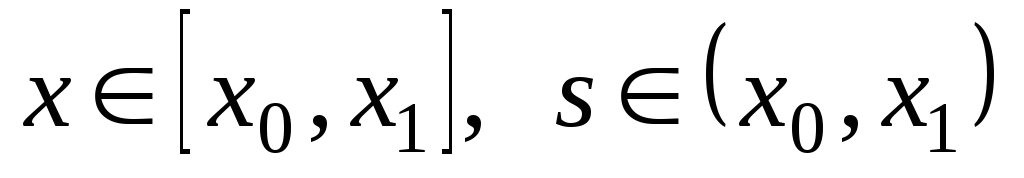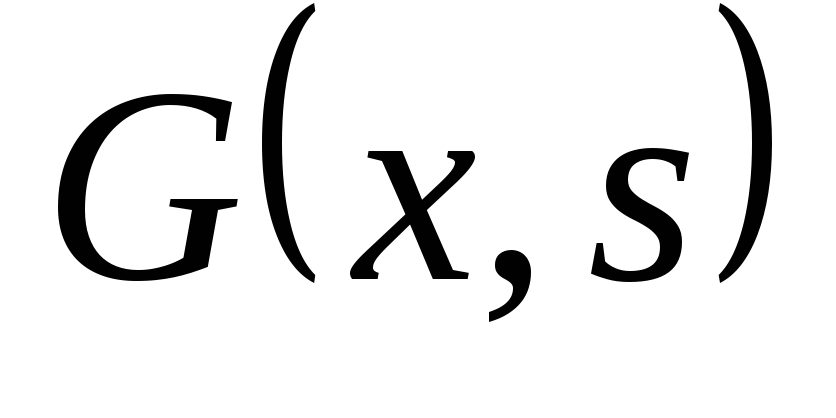2. является при 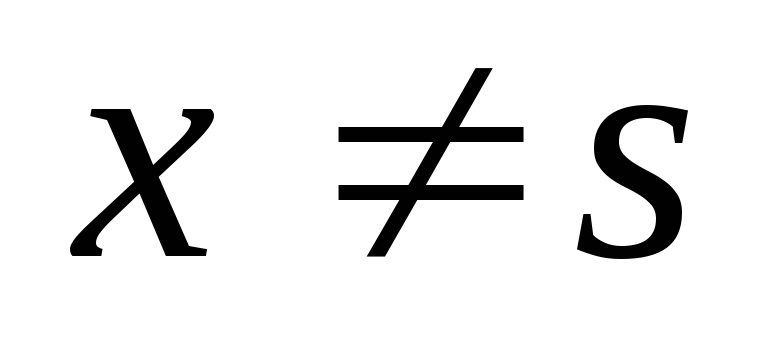решением соответствующего однородного уравнения:

. (95)

3. удовлетворяет нулевым краевым условиям: 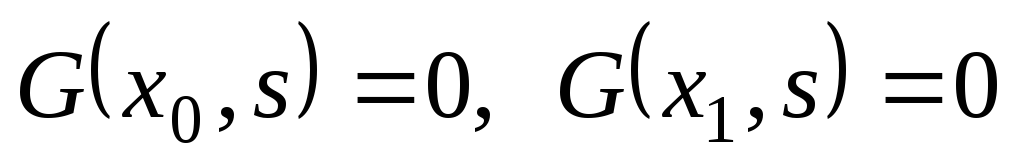. (96)

4. В точке x = s производная 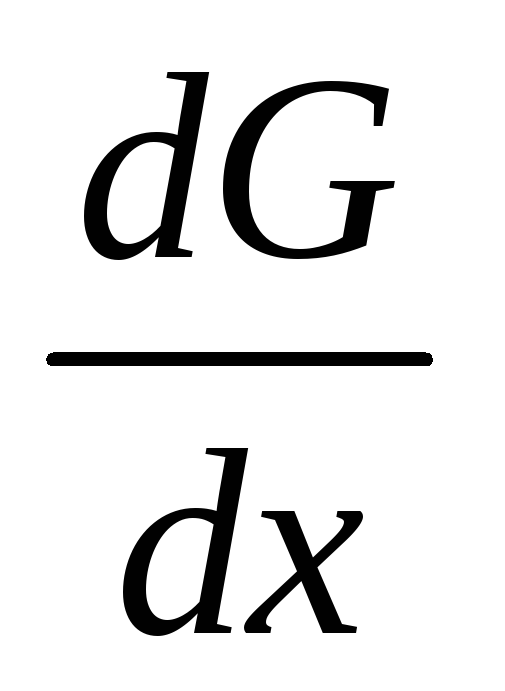имеет разрыв первого рода со скачком :

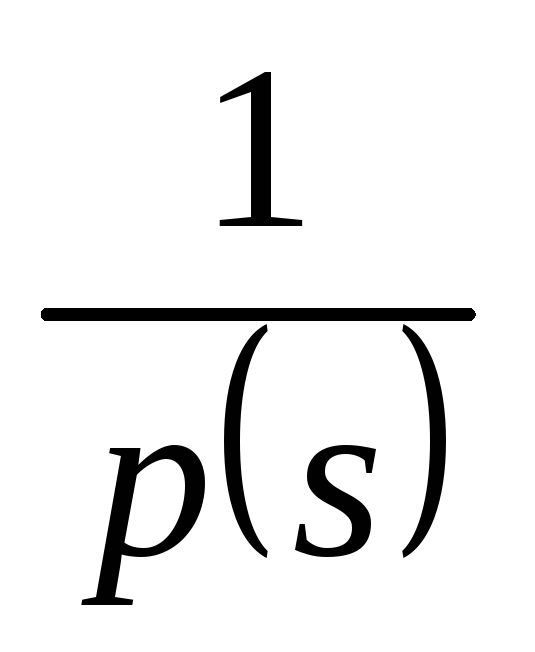. (97)

Функция , удовлетворяющая условиям 1.-4., называется функцией Грина краевой задачи (94). Если функция Грина существует, то решение краевой задачи (94) также существует и имеет вид

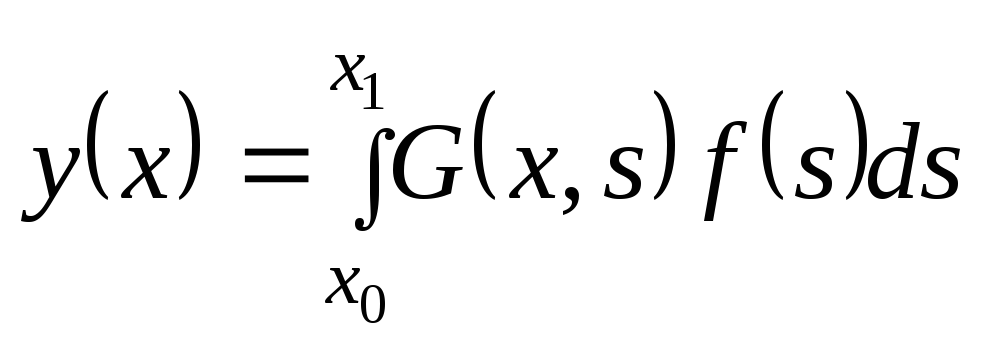. (98)

Функция Грина строится согласно формулы

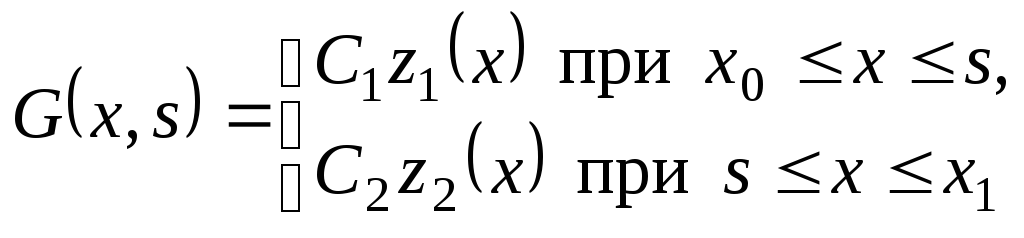
где z₁(x) – решение задачи Коши:

;

z₂(x) – решение задачи Коши:

;

;

W(z₁(s), z₂(s)) = W(s) – определитель Вронского.

Таким образом, формула для построения функции Грина имеет вид:

. (99)

Краевая задача для функции у может быть записана в общем виде так

где - заданные числа, а - непрерывные на интервале функции, причем .

Пример 47. Найти решение уравнения: , удовлетворяющее условиям: .

▲ Из краевых условий исходной задачи, для функции Грина имеем задачу: уравнение (95) принимает вид

краевые условия (96) будут выглядеть следующим образом

,

а условие (97)

.

Интегрируя уравнение один раз, находим

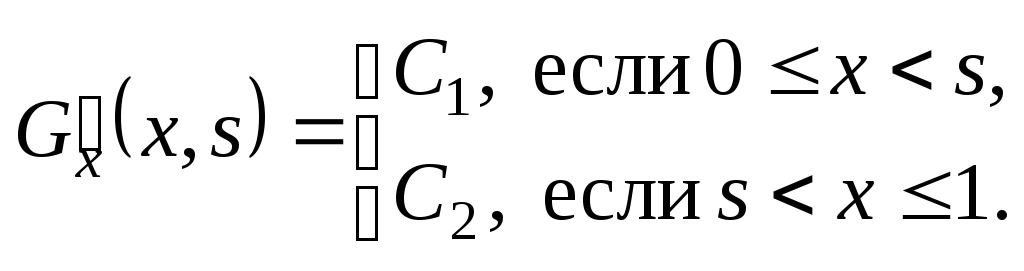
Здесь , так как по условию производная терпит разрыв при x = s. Далее, интегрируя , получаем

(*)

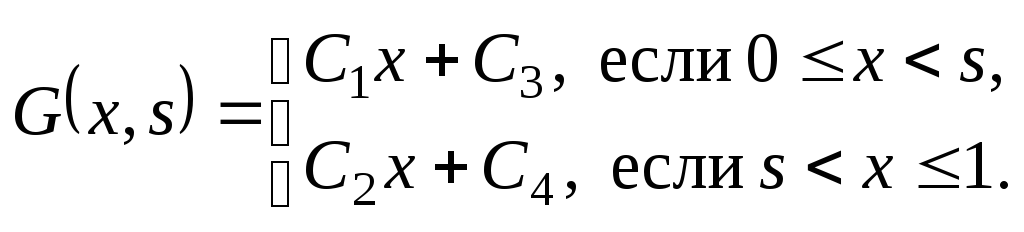Поскольку функция G непрерывная, то должно выполняться условие

. (**)

Из краевых условий для функции G следует, что

(***)

Условие скачка производной при x = s приобретает вид

. (****)

Решив систему уравнений (**) – (****) относительно постоянных , получим

Подставив в (*), закончим построение функции Грина для предложенной краевой задачи:

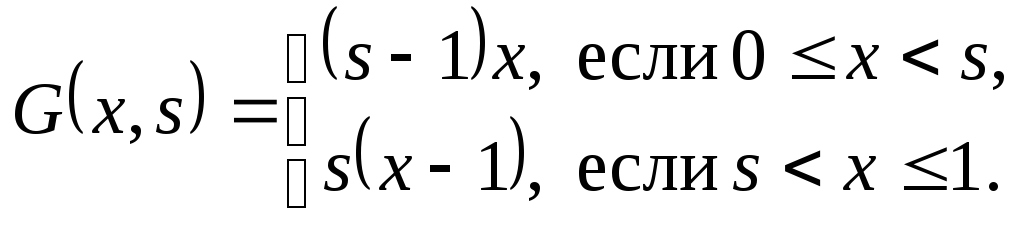
Решение поставленной краевой задачи будет иметь вид

.▲

Пример48. Найти функцию Грина для краевой задачи:

.

▲ Для функции Грина запишем дифференциальное уравнение

.

Используя подстановку , где , приведем это уравнение к виду:

.

Последовательно интегрируя его, получаем

.

Если ввести в рассмотрение функцию Ф как - , то функцию U можно представить также в виде . Следовательно,

(*)

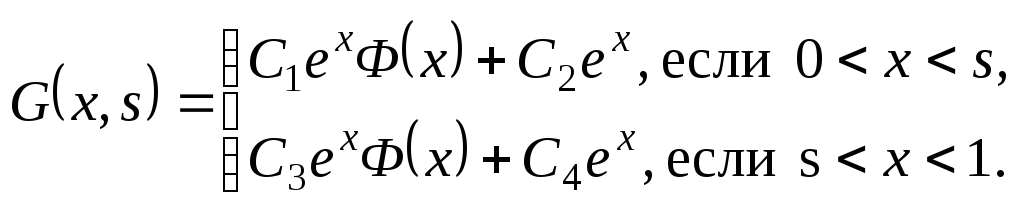Запишем теперь систему уравнений относительно C_i (i = 1,2,3,4):

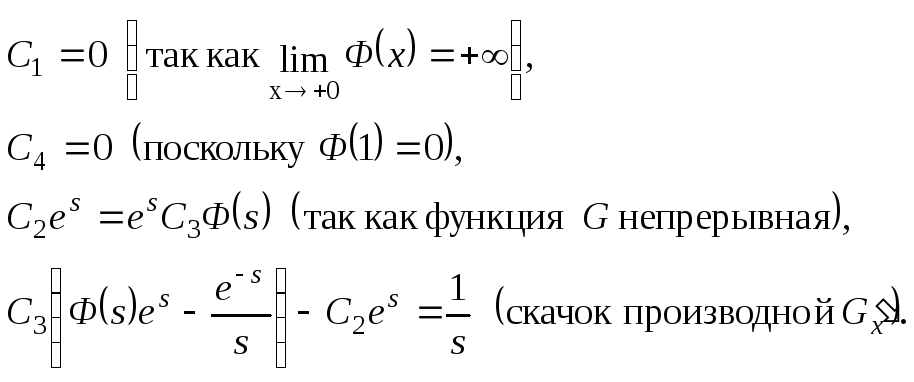
Решив систему и подставив значения C_i в (*), окончательно получим

▲