2.5.Оптимальные оценки ресурсов и методы их получения. Двойственная задача линейного программирования и ее связь с основной задачей

Рассмотрим модель производственной системы (2.7)-(2.9) с точки зрения ценности имеющихся у предприятия ресурсов. Будем иметь в виду, что ресурсы, которые в оптимальном плане не используются полностью, имеют для производственной системы низкую ценность в том смысле, что предприятие не будет согласно нести даже небольшие расходы на увеличение запасов этих ресурсов. Так, дорогое оборудование, не используемое в технологическом процессе, имеет для предприятия нулевую ценность. Наибольшую ценность будут иметь те ресурсы, которые в наибольшей степени ограничивают выпуск продукции, а, следовательно, и доход предприятия, и на увеличение запасов которых предприятие согласно нести значительные расходы.

В связи с этим можно считать, что каждый вид ресурса обладает некоторой “теневой ценой”, определяющей ценность данного ресурса для предприятия с точки зрения дохода от реализации выпускаемой продукции и зависящей от наличного запаса этого ресурса и потребности в нем для выпуска продукции.

Если предприятие ограничивается одним производственным способом, требующим больших затрат некоторого ресурса, запасы которого ограничены, то теневая цена этого ресурса будет велика. Однако установленные в соответствии с этим способом производства теневые цены не будут наилучшими, так как введение других производственных способов позволяет более рационально использовать все запасы ресурсов. Например, если в модели из предыдущего пункта ограничиться способом Р₂, то теневая цена капитала будет очень высокой, а теневая цена труда крайне низкой (при двух единицах капитала его останется 7 единиц). Если же наряду с Р₂ ввести способ производства Р₃ , то теневая цена капитала останется прежней, а теневая цена труда повысится (при двух единицах капитала его останется 2 единицы).

Ясно, что оптимальному состоянию производственной системы в модели (2.7)-(2.9) соответствует вектор оптимальных теневых цен наличного запаса ресурсов. Оптимальные теневые цены называют объективно обусловленными оценками (о.о.о.) или оптимальными оценками, или двойственными оценками ресурсов.

Для определения о.о.о. ресурсов составим самостоятельную задачу линейного программирования.

Обозначим через у_i ( i =1,2,..., m) о.о.о. i-го ресурса. Величины у_i должны быть такими, чтобы сумма теневых цен ресурсов, затрачиваемых при любом используемом производственном способе, не была меньше величины дохода р_j :

Если производственная система находится в оптимальном состоянии, то ресурсы потребляются в соответствии с их о.о.о., а их суммарная теневая цена является наименьшей возможной

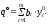
Таким образом, задача определения о.о.о. ресурсов формулируется как следующая оптимизационная задача:

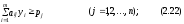
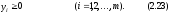
Задача линейного программирования (2.21)-(2.23) называется двойственной задачей по отношению к задаче (2.7)-(2.9). Прямая и двойственная задачи тесно связаны между собой. Эта связь заключается в следующем:

если прямая задача является задачей на максимум, то двойственная задача — на минимум;

коэффициенты целевой функции в прямой задаче являются свободными членами в ограничениях двойственной задачи и, наоборот, свободные члены из ограничений прямой задачи являются коэффициентами целевой функции двойственной задачи;

коэффициенты при переменных в ограничениях двойственной задачи являются столбцами матрицы коэффициентов ограничений прямой задачи;

знаки неравенств в системе ограничений прямой задачи меняются на противоположные в системе ограничений двойственной задачи.

Установим связь между решениями прямой и двойственной задач линейного программирования.

Также как и в предыдущем пункте, примем в прямой задаче переменные x₁,..., x_n за свободные и сформулируем ее в виде модели (2.11), (2.12), (2.9), обозначив переменные группы t_i через переменные x_{n+ i} :

с = 0 -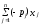 max;

x_{n+ i} = b_i - , x_{n+ i}   (i=1,2,..., m);

х_j  0 (j=1,2,..., n).

Этой задаче соответствует матрица коэффициентов

. (2.24)

В двойственной задаче примем за свободные переменные у₁ ,..., у_m и сформулируем ее в следующем виде:

q = 0 +

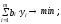
у_{m+ j} = -

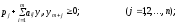
у _i  ; ( i =1,2,..., m).

Отметим, что экономическое содержание переменных у_{m+ j} — превышение теневой цены вектора затрат по i-му производственному способу над доходами, выраженными в величине выпуска р _j.

Этой задаче соответствует матрица коэффициентов:

. (2.25)

Столбцы матрицы (2.25) являются строками матрицы (2.24), Следовательно, прямая и двойственная задачи описываются одной и той же матрицей, в которой должно быть установлено следующее соответствие между переменными:

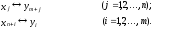(2.26)

Отметим, что любое преобразование матрицы (2.24) по правилам симплекс процедуры приводит к новой матрице, которая описывает новое допустимое (или оптимальное) решение как прямой, так и двойственной задач.

Отсюда следуют важные соотношения, выражающие математические свойства решений прямой и двойственной задач:

1)равенство экстремальных значений целевых функций (верхний левый угол таблиц коэффициентов в последней симплекс-таблице):

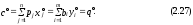
2) свободные переменные в оптимальном решении прямой задачи (принимают нулевое значение) соответствуют (в силу 2.26) базисным переменным оптимального решения двойственной задачи (принимают положительные значения) и наоборот. Таким образом, справедливы следующие соотношения “допол-няющей нежесткости”:

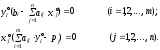(2.28)

Дадим краткую экономическую интерпретацию соотношений (2.27) — первая теорема двойственности и (2.28) — вторая теорема двойственности. Более подробно экономическое содержание двойственных оценок излагается в главе 3.

Итак, соотношение (2.27) показывает, что в оптимальном состоянии суммарный выпуск предприятия совпадает с затратами производственных ресурсов, исчисленными в их теневых ценах. Первое из соотношений (2.28) показывает, что, если i-й производственный ресурс является недефицитным (т.е. выражение в круглых скобках строго положительно), то его теневая цена равна нулю. Наконец, второе из соотношений (2.28) показывает, что если j-й производственный способ является интенсивным, т.е. 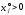, то величина выпуска р _j совпадает с затратами производственных ресурсов по этой технологии.