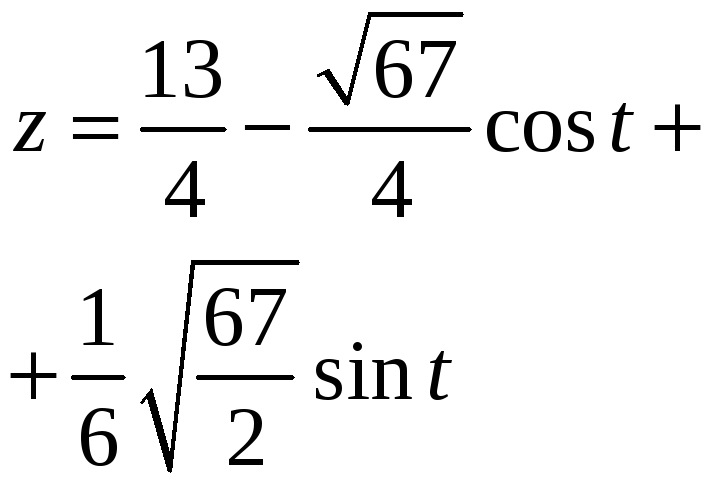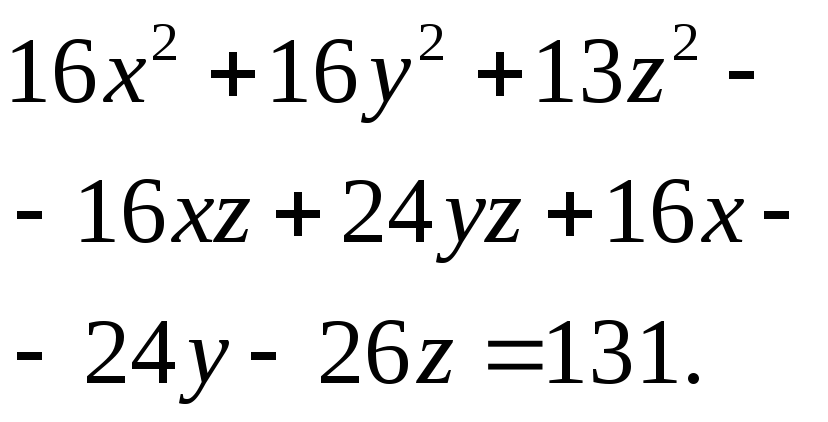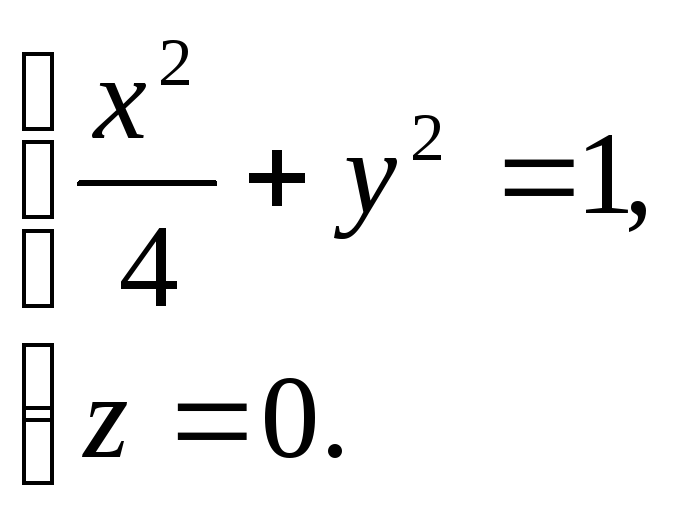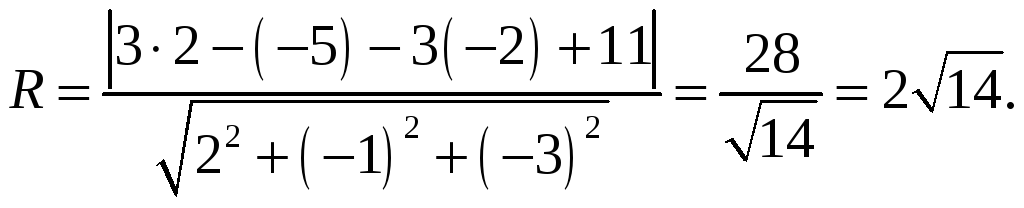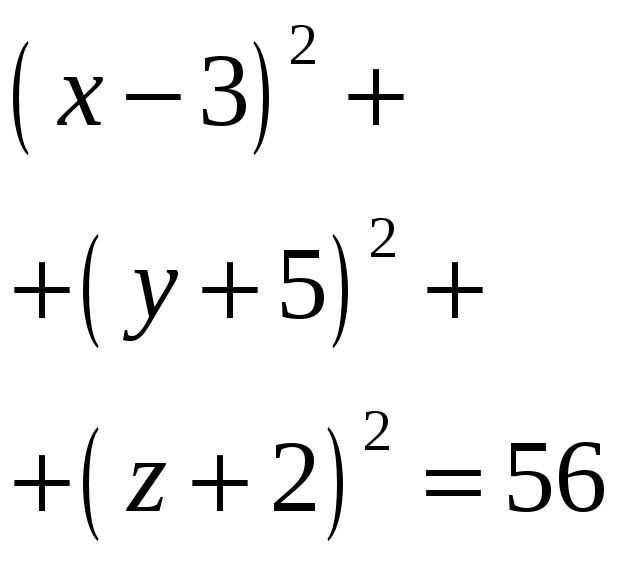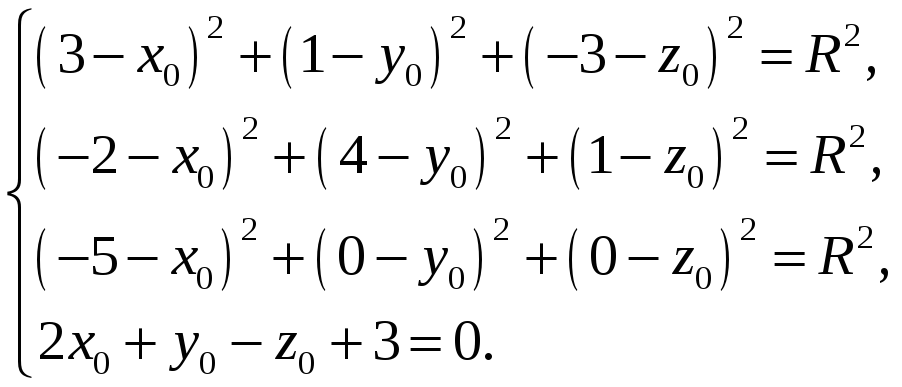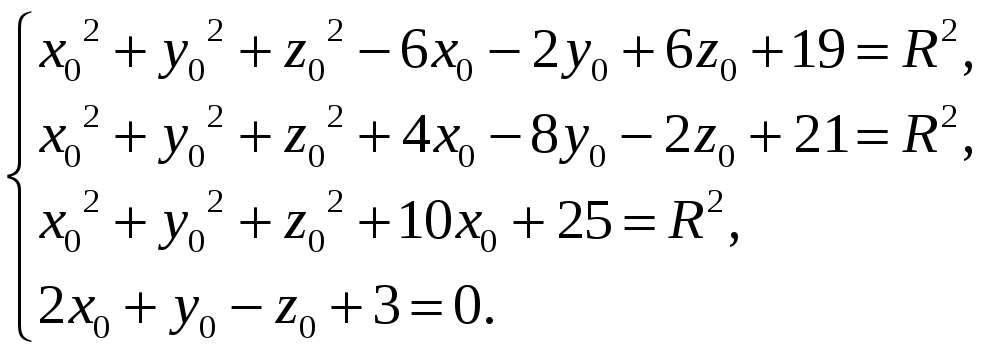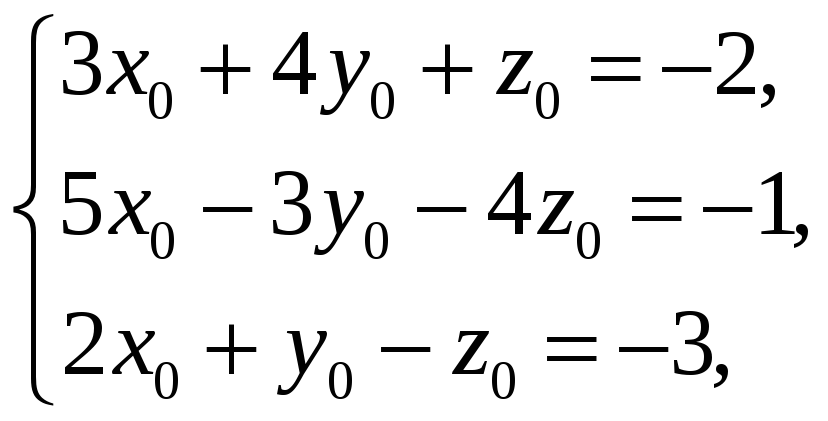Практическое занятие 4
|
Поверхности второго порядка |
||
|
1 |
Установите
тип поверхности, заданной уравнением
Решение: Перенесем константу в правую часть уравнения и разделим обе части уравнения на число 4. Получим
Это уравнение задает двуполостный гиперболоид вращения с осью OY. |
Дву-полостный гиперболоид |
|
2 |
Установите
тип поверхности, заданной уравнением
Решение: Преобразуем уравнение к виду
являющемуся канонической формой уравнения параболоида вращения с осью OZ, вершина которого находится в точке (0;0;2), а выпуклость обращена вверх. |
Параболоид |
|
3 |
Установите тип указанной поверхности и постройте ее:
1)
2)
3)
4)
5)
|
1) параболоид вращения; 2) ось oz;
3)
две пересекаю-щиеся плоскости
4)
две плоскости
5) круговой цилиндр с образующей, параллельной оси oy.
|
|
4 |
Составьте уравнения проекций на координатные плоскости сечения эллиптического параболоида
плоскостью
Решение: Сечение параболоида плоскостью задается системой уравнений
Этой системе
соответствует некоторая линия в
пространстве. Чтобы найти проекцию
этой линии на координатную плоскость
OXY,
следует исключить из этой системы
переменную z.
В результате
получаем
На плоскость
OXY:
|
|
|
5 |
Составьте уравнение поверхности, образованной вращением кривой
вокруг оси OX. Решение: Сечение
искомой поверхности плоскостью
|
|
|
6 |
Найдите
общие точки поверхности
Решение: Выделим полные квадраты переменных в уравнении поверхности и увидим,
что
она представляет собой сферу
Перейдем
к параметрическим уравнениям прямой
Подстановка этих значений переменных в уравнение поверхности приводит к квадратному уравнению для t c отрицательным дискриминантом. Следовательно, действительных значений t не существует, и поверхность не имеет общих точек с прямой, которая проходит вне сферы. |
Нет |
|
7 |
Найдите
общие точки поверхности
Решение:
Общие
точки поверхностей удовлетворяют
системе
Приравнивая
значения 2z
, выраженные из этих уравнений, получим,
что
|
Эллипс
|
|
8 |
Составьте
уравнение цилиндра, образующие
которого параллельны вектору
Решение:
Множество точек
искомой поверхности образовано
точками, лежащими на прямых, проходящих
через некоторую точку направляющей
параллельно вектору
|
|
|
9 |
Составьте уравнение конуса с вершиной в точке S(0;0;5) и направляющей
Решение: Множество
точек искомой поверхности образовано
точками, лежащими на прямых, проходящих
через некоторую точку направляющей
и точку S.
Составим канонические уравнения этих
прямых
|
|
|
10 |
Составьте
уравнение сферы с центром в точке
(3,-5,-2), если плоскость
Решение: Расстояние от центра сферы до касательной плоскости равно радиусу сферы:
Уравнение сферы:
|
|
|
11 |
Составьте
уравнение сферы, проходящей через
точки
Решение:
Запишем уравнение
сферы в виде
Раскрывая скобки, получаем
Вычитая из третьего уравнения второе и из второго первое, для координат центра сферы получаем равносильную систему
откуда
|
|
|
12 |
Методом сечений исследуйте поверхность, заданную уравнением
Решение: Перепишем уравнение поверхности в виде
и рассмотрим
сечения поверхности плоскостями
Приводя к каноническому виду, имеем
– уравнение
гиперболы,
Итак,
поверхность может быть получена
вращением гиперболы относительно ее
мнимой оси, т.е. поверхность –
однополостный гиперболоид вращения,
|
Однопо-лостный гиперболоид вращения |

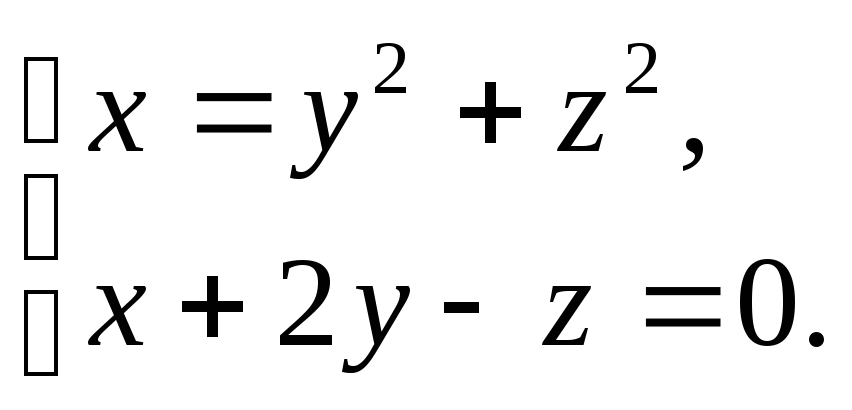
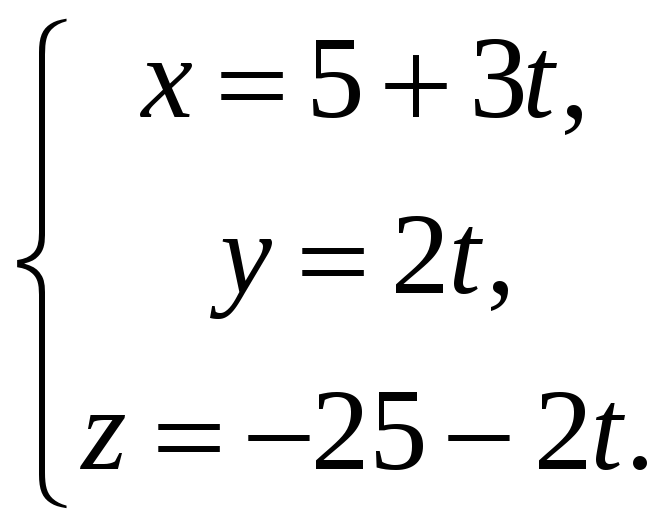
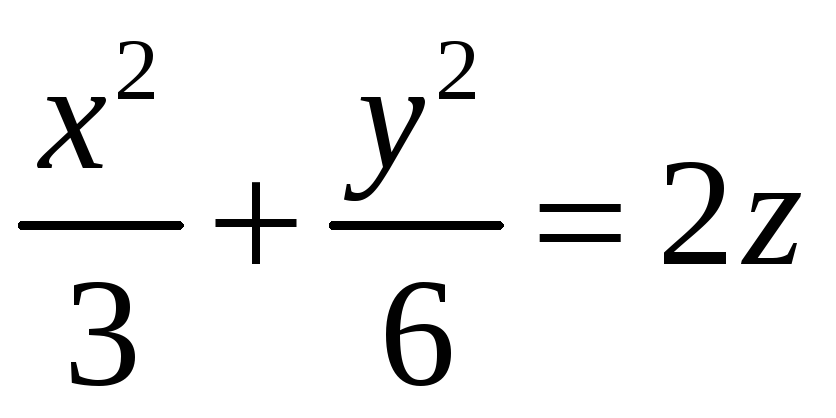 и плоскости
и плоскости
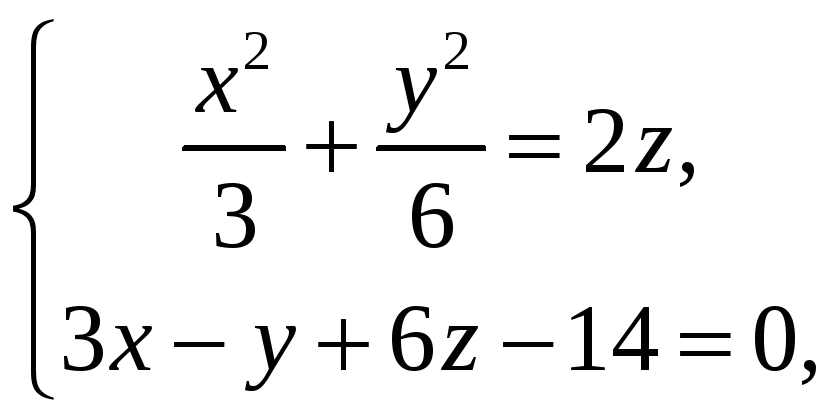
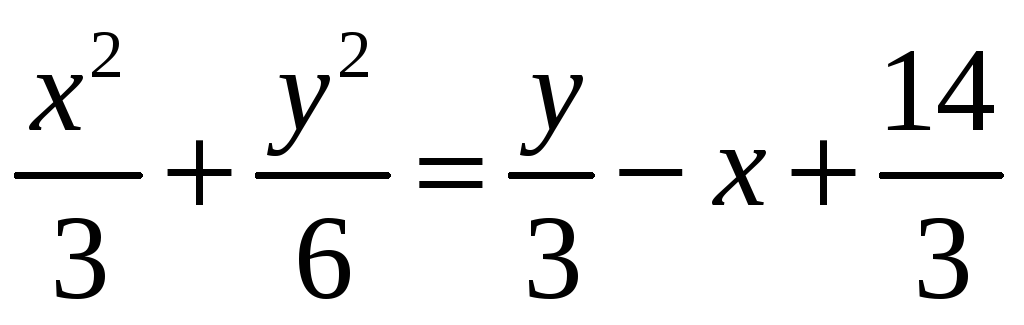 .
Выделение полных квадратов переменных
приводит к уравнению эллипса
.
Выделение полных квадратов переменных
приводит к уравнению эллипса
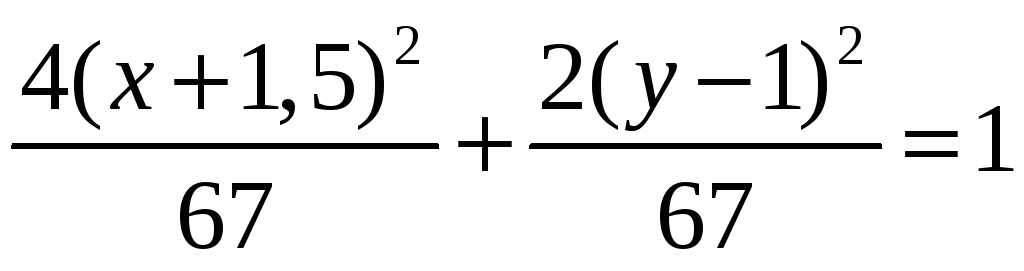 ,
который является проекцией линии
пересечения эллиптического параболоида
и плоскости на координатную плоскость
,
который является проекцией линии
пересечения эллиптического параболоида
и плоскости на координатную плоскость
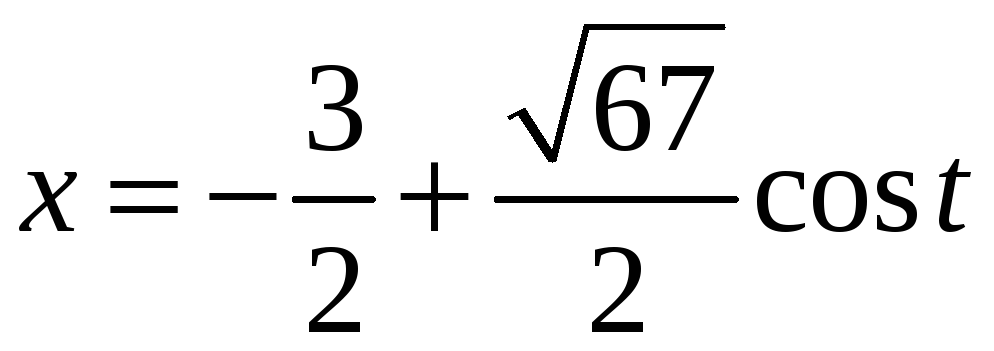 ,
,
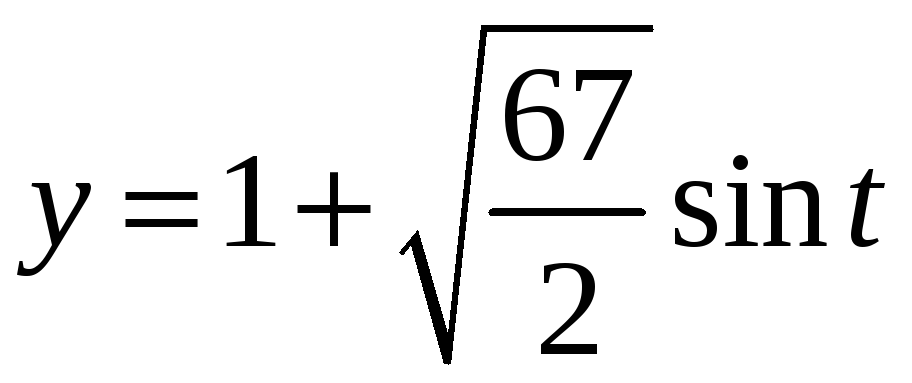 .
Подставляя эти выражения в уравнение
плоскости, получаем
.
Подставляя эти выражения в уравнение
плоскости, получаем
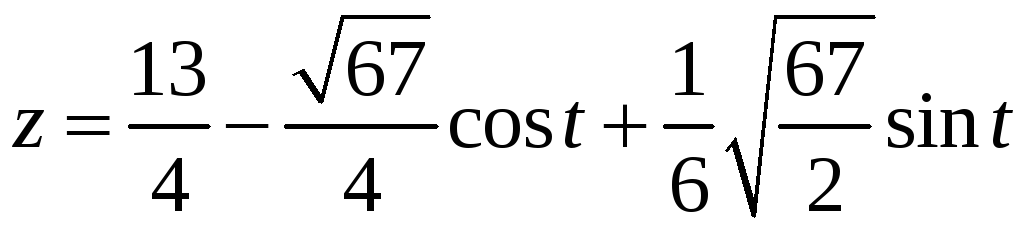 .
Линия – эллипс.
.
Линия – эллипс.