
- •Экономико-математические методы и модели: оптимизационные методы и модели
- •1. Введение
- •2. Общая задача математического программирования. Формы записи задач линейного программирования
- •3. Составление математических моделей простейших экономических задач
- •3. Задание целевой функции.
- •3. Задание целевой функции.
- •4. Графический метод решения задачи линейного программирования
- •4.1. Геометрическая интерпретация задачи линейного программирования
- •4.2. Алгоритм графического решения задачи линейного программирования
- •5. Симплексный метод решения задач линейного программирования
- •Построение математической модели экономической задачи.
- •3. Задание целевой функции.
- •2. Построение начального опорного плана.
- •3. Построение первоначальной симплекс-таблицы.
- •4. Вычисление оценок (значений критерия оптимальности плана).
- •Критерий оптимальности опорного плана
- •Критерий единственности опорного плана
- •5. Симплекс-критерии перехода к новому опорному плану.
- •Симплекс-критерий I включения вектора в базис
- •Симплекс-критерий II исключения вектора из базиса
- •6. Алгоритм перехода к новому базису.
- •6. Алгоритм решения задачи симплексным методом
- •6. Метод искусственного базиса
- •Особенности метода искусственного базиса
- •7. Транспортная задача (тз) линейного программирования
- •7.1. Постановка и математическая модель транспортной задачи
- •7.2. Алгоритм решения транспортной задачи
- •7.3. Опорный план транспортной задачи
- •7.3.1. Метод вычеркивания проверки опорности плана (образования цикла)
- •7.4. Построение начального опорного плана транспортной задачи
- •7.4.1. Метод северо-западного угла
- •7.4.2. Метод минимальной стоимости
- •Запишем математическую модель поставленной задачи.
- •2. Построение начального опорного плана методом минимальной стоимости.
- •Метод потенциалов.
- •Вычисление потенциалов
- •Проверка оптимальности плана
- •Переход от одного опорного плана к другому
5. Симплексный метод решения задач линейного программирования
Графический метод наглядно
иллюстрирует свойства решений задач
линейного программирования, которые
справедливы и в случае произвольного
числа переменных
![]() при
при
![]() (рис.1-3).
(рис.1-3).
Теорема 1. Для того чтобы задача
линейного программирования имела
оптимальные решения (план) необходимо
и достаточно, чтобы многогранник
допустимых решений (планов) содержал
хотя бы одну точку, а целевая функция
![]() была ограничена снизу при решении задач
минимизации или сверху при решении
задач максимизации.
была ограничена снизу при решении задач
минимизации или сверху при решении
задач максимизации.
Теорема 2. Если задача линейного программирования имеет оптимальный план, то он достигается в вершине многогранного тела, которое является областью допустимых планов (решений).
Если оптимальный план достигается более чем в одной вершине, то он достигается в любой точке выпуклой линейной комбинации соответствующих вершин.
Рассмотрим каноническую задачу
линейного программирования, система
ограничений которой состоит из
![]() уравнений с
уравнений с
![]() неизвестными
неизвестными
![]() ,
(17)
,
(17)
![]() ,
(18)
,
(18)
![]() .
(19)
.
(19)
Будем считать, что правые части всех
уравнений системы ограничений (18)
неотрицательны
![]() .
Если в каком-либо уравнении правая часть
отрицательна, то это уравнение нужно
умножить на
.
Если в каком-либо уравнении правая часть
отрицательна, то это уравнение нужно
умножить на
![]() .
.
Запишем задачу (17)-(19) в векторной форме.
![]() ,
(20)
,
(20)
![]() ,
(21)
,
(21)
![]() (22)
(22)
где
![]() -
вектор-строка
-
вектор-строка
![]() коэффициентов целевой функции;
коэффициентов целевой функции;
![]() -
вектор-столбец
-
вектор-столбец
![]() переменных задачи;
переменных задачи;
![]() - вектор-столбец
- вектор-столбец
![]() правых частей системы ограничений (18),
которой в экономике называют вектором
запасов;
правых частей системы ограничений (18),
которой в экономике называют вектором
запасов;
![]() - вектора-столбцы коэффициентов при
переменных или вектора условий:
- вектора-столбцы коэффициентов при
переменных или вектора условий:
![]() ,
(23)
,
(23)
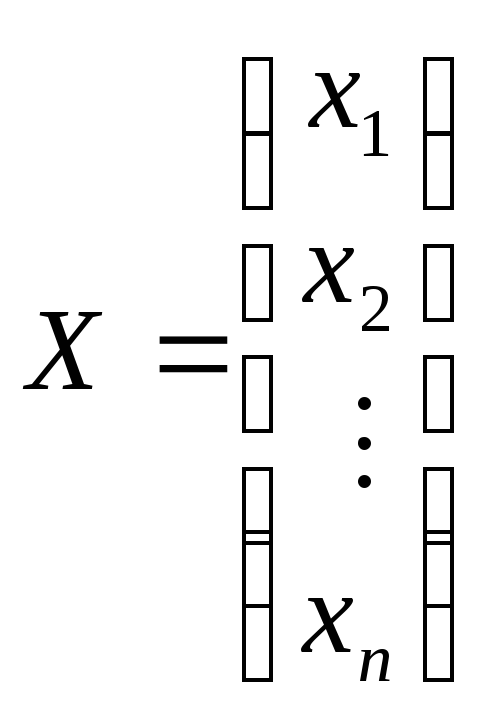 ,
,
 ,
(24)
,
(24)
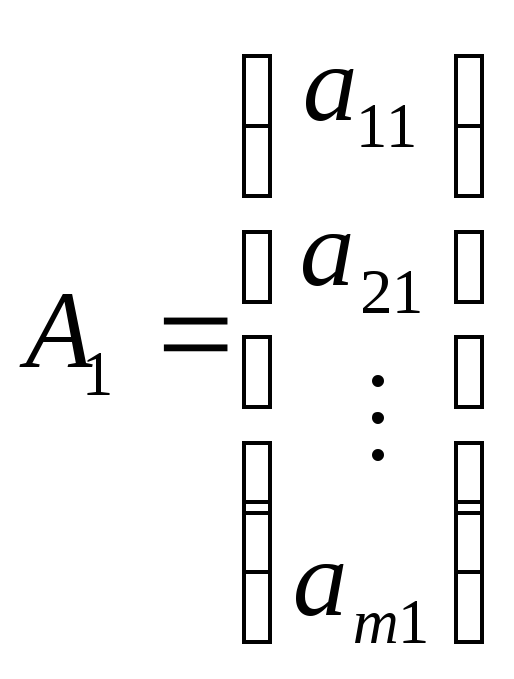 ,
,
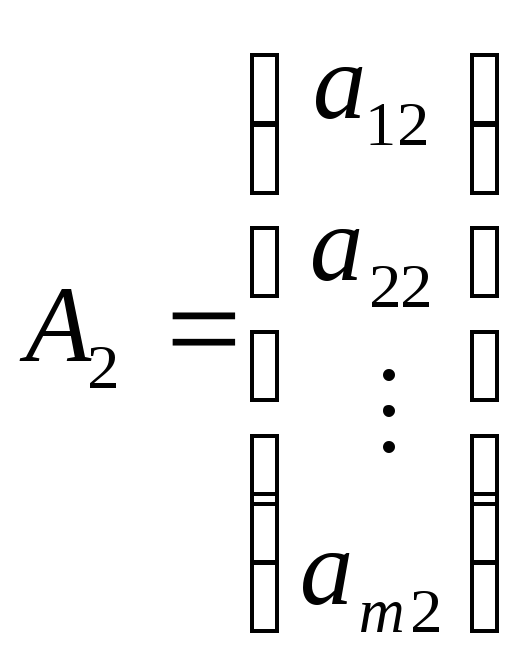 ,
,
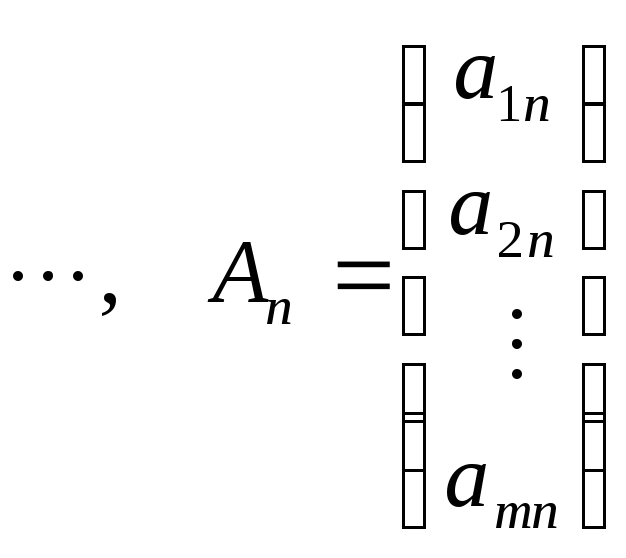 .
(25)
.
(25)
В соответствие с теоремой 1, для
существования оптимального решения
задачи (20)-(22) многогранник допустимых
планов должен содержать хотя бы одну
точку – быть не пустым множеством. Это
означает, что система линейных неоднородных
уравнений-ограничений (21) должна быть
совместна в области неотрицательных
значений переменных
![]() задачи. При этом максимальное количество
линейно-независимых векторов системы
из
задачи. При этом максимальное количество
линейно-независимых векторов системы
из
![]() векторов-условий
векторов-условий
![]() ,
равно рангу
,
равно рангу
![]() системы уравнений (21). Они образуют базис
данной системы, а их количество должно
быть меньше числа переменных
системы уравнений (21). Они образуют базис
данной системы, а их количество должно
быть меньше числа переменных
![]() задачи:
задачи:
![]() .
.
Напомним, что любой вектор
![]() можно единственным образом разложить
по векторам базиса:
можно единственным образом разложить
по векторам базиса:
![]() ,
,
где
![]() - координаты (коэффициенты разложения)
вектора
- координаты (коэффициенты разложения)
вектора
![]() в данном базисе.
в данном базисе.
Система из
![]() единичных векторов
единичных векторов

линейно-независимая и является одним
из базисов пространства
![]() -мерных
векторов.
-мерных
векторов.
Пусть ранг
![]() системы уравнений (21) равен числу
системы уравнений (21) равен числу
![]() уравнений:
уравнений:
![]() .
Для определенности положим, что
линейно-независимыми являются первые
.
Для определенности положим, что
линейно-независимыми являются первые
![]() столбцов. Тогда соответствующие данным
векторам
столбцов. Тогда соответствующие данным
векторам
![]() переменные
переменные
![]() будут базисными, а остальные
будут базисными, а остальные
![]() переменных
переменных
![]() - свободными. Перенеся свободные
переменные в правую часть системы
уравнений (21), получим систему из
- свободными. Перенеся свободные
переменные в правую часть системы
уравнений (21), получим систему из
![]() уравнений относительно
уравнений относительно
![]() базисных неизвестных
базисных неизвестных
![]() .
Придавая свободным неизвестным
.
Придавая свободным неизвестным
![]() произвольные числовые значения и находя
значения базисных переменных
произвольные числовые значения и находя
значения базисных переменных
![]() (например, по правилу Крамера), получим
бесконечное множество решений
(например, по правилу Крамера), получим
бесконечное множество решений
![]() системы (21).
системы (21).
Из бесконечного множества решений (планов) нас интересуют только те, которые удовлетворяют условиям (22) неотрицательности переменных задачи и правых частей системы ограничений.
Определение. Опорным планом
задачи линейного программирования
называется такое допустимое решение
![]() ,
для которого базисные переменные
неотрицательны, а свободные переменные
равны нулю:
,
для которого базисные переменные
неотрицательны, а свободные переменные
равны нулю:
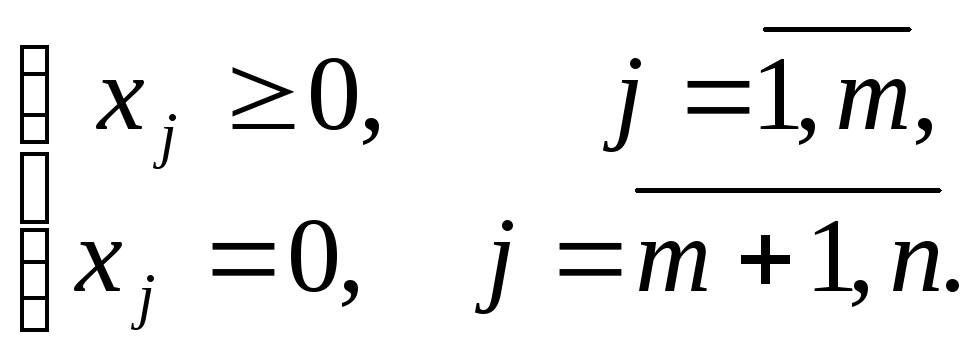
Определение. Опорный
план называется вырожденным,
если число отличных от нуля базисных
переменных меньше
![]() ,
и невырожденным -
если их число равно
,
и невырожденным -
если их число равно
![]() .
.
Итак, в опорном плане базисные переменные
неотрицательны
![]() и соответствуют линейно-независимым
векторам
и соответствуют линейно-независимым
векторам
![]() системы ограничений (21) . Количество
системы ограничений (21) . Количество
![]() положительных компонентов
положительных компонентов
![]() в опорных планах не превышает ранга
в опорных планах не превышает ранга
![]() системы ограничений.
системы ограничений.
С геометрической точки зрения область
допустимых планов (решений) задачи
линейного программирования с произвольным
числом переменных
![]() и ограничений
и ограничений
![]() представляет собой выпуклую многогранную
область или замкнутое многогранное
тело, а опорные планы – вершины этого
многогранного тела. Для случая двух
переменных это показано на рисунках
1-3.
представляет собой выпуклую многогранную
область или замкнутое многогранное
тело, а опорные планы – вершины этого
многогранного тела. Для случая двух
переменных это показано на рисунках
1-3.
Теорема. Каждому опорному плану
![]() соответствует вершина многогранника
решений и наоборот, каждой вершине
многогранника решений соответствует
опорный план
соответствует вершина многогранника
решений и наоборот, каждой вершине
многогранника решений соответствует
опорный план
![]() .
.
Выводы
На основании приведенных теорем следует.
1. Если область допустимых решений не пустая (содержит хотя бы одну точку), а целевая функция ограничена в направлении поиска экстремума, то задача линейного программирования имеет оптимальное решение и существует такая вершина многогранника решений, в которой целевая функция достигает своего наибольшего или наименьшего значения.
2. Каждой угловой точке многогранника решений соответствует опорный план.
3. Каждый опорный план определяется
системой
![]() линейно-независимых базисных векторов,
содержащихся в системе
линейно-независимых базисных векторов,
содержащихся в системе
![]() векторов-ограничений
векторов-ограничений
![]() .
.
4. Оптимальный план является одним из опорных планов. Для нахождения оптимального плана необходимо исследовать только опорные планы.
5. Максимальное количество опорных
планов задачи равно числу сочетаний
![]() .
При большом количестве переменных
.
При большом количестве переменных
![]() и ограничений
и ограничений
![]() нахождение оптимального плана путем
перебора опорных планов затруднительно.
нахождение оптимального плана путем
перебора опорных планов затруднительно.
6. Необходимо иметь алгоритм упорядоченного перехода от одного опорного плана к другому, позволяющий за минимальное количество шагов найти оптимальный план либо его отсутствие.
Таким алгоритмом является симплексный метод.
Симплексный метод – это итерационная (пошаговая) процедура нахождения оптимального плана или установления его отсутствия.
Идея метода заключается в последовательном приближении целевой функции к оптимальному значению путем целенаправленного перехода от одного опорного плана задачи к другому.
Основным содержанием симплексного метода являются:
1) процедура построения начального опорного плана;
2) процедура перехода от одного опорного плана к другому, на котором значения целевой функции ближе к оптимальному плану;
3) критерии завершения решения задачи: критерий оптимальности плана и критерий отсутствия решения.
Рассмотрим алгоритм симплекс-метода на примере решения следующей задачи.
Задача. При изготовлении,
каждый из четырех видов продукции
![]() ,
,
![]() ,
,
![]() и
и
![]() проходит последовательную обработку
на двух станках. В таблице 3 представлены
длительность обработки единицы продукции
каждого вида, цена машино-часа, лимит
(ограничение) времени работы станков,
а также цена реализации единицы
продукции.
проходит последовательную обработку
на двух станках. В таблице 3 представлены
длительность обработки единицы продукции
каждого вида, цена машино-часа, лимит
(ограничение) времени работы станков,
а также цена реализации единицы
продукции.
Таблица 3.
|
Станок |
Длительность
обработки
|
Лимит использования станков (час) |
Цена машино-часа (у.е.) |
|||
|
|
|
|
|
|||
|
1 2 |
2 3 |
3 2 |
4 1 |
2 2 |
450 380 |
10 15 |
|
Цена ед. продукции (у.е) |
73 |
70 |
55 |
45 |
|
|
Затраты на производство единицы продукции каждого вида считаются пропорциональными времени использования станков.
Найти оптимальный план производства всех видов продукции, который обеспечивает максимальную прибыль.
