Модель чорного ящика

В целях исследований часто бывает удобно представить исследуемый объект в виде ящика, имеющего входы и выходы, не рассматривая детально его внутренней структуры. Конечно, преобразования в ящике (на объекте) происходят (сигналы проходят по связям и элементам, меняют свою форму и т. п.), но при таком представлении они происходят скрыто от наблюдателя.

По степени информированности исследователя об объекте возможно деление объектов на три типа «ящиков»:

• «белый ящик»: об объекте известно все;

• «серый ящик»: известна структура объекта, не известны количественные значения параметров;

• «черный ящик»: об объекте не известно ничего.

Черный ящик условно изображают как на рис ниже.

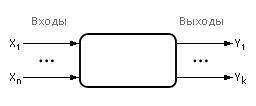
Рис. Изображение черного ящика

Значения на входах и выходах черного ящика можно наблюдать и измерять. Содержимое ящика неизвестно.

Регресійний аналіз

Задача состоит в том, чтобы, зная множество значений на входах и выходах, построить модель, то есть определить функцию ящика, по которой вход преобразуется в выход. Такая задача называется задачей регрессионного анализа.

В зависимости от того, доступны входы исследователю для управления или только для наблюдения, можно говорить про активный или пассивный эксперимент с ящиком.

Д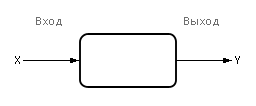ля начала, предположим, что мы имеем дело с черным ящиком, имеющим один вход и один выход.

Одномерная модель черного ящика

Линейная одномерная модель

Допустим для простоты, что зависимость между входом и выходом линейная или почти линейная. Тогда данная модель будет называться линейной одномерной регрессионной моделью. Иными словами, рассматривая экспериментально полученные данные, предположим, что они подчиняются линейной гипотезе, то есть выход Y зависит от входа X линейно:

Y = A₀ + A₁X .

П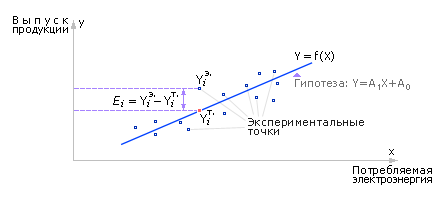усть, например, перед нами стоит задача определить, как зависит выпуск продукции от количества потребляемой электроэнергии. Результаты наблюдений отобразим на графике. Всего на графике n экспериментальных точек, которые соответствуют n наблюдениям.

Графическое изображение множества экспериментальных точек и линейной гипотезы

Определение неизвестных коэффициентов A₀ и A₁ линейной одномерной модели

Для каждой из n снятых экспериментально точек вычислим ошибку (E_i) между экспериментальным значением (Y_i^Эксп.) и теоретическим значением (Y_i^Теор.), лежащим на гипотетической прямой A₁X + A₀ (см. рис. выше):

E_i = (Y_i^Эксп. – Y_i^Теор.), i = 1, …, n;

E_i = Y_i – A₀ – A₁ · X_i, i = 1, …, n.

Ошибки E_i для всех n точек следует сложить. Чтобы положительные ошибки не компенсировали в сумме отрицательные, каждую из ошибок возводят в квадрат и складывают их значения в суммарную ошибку F уже одного знака:

E_i² = (Y_i – A₀ – A₁ · X_i)², i = 1, …, n.

Цель метода — минимизация суммарной ошибки F за счет подбора коэффициентов A₀, A₁. Другими словами, это означает, что необходимо найти такие коэффициенты A₀, A₁ линейной функции Y = A₁X + A₀, чтобы ее график проходил как можно ближе одновременно ко всем экспериментальным точкам. Поэтому данный метод называется методом наименьших квадратов.

С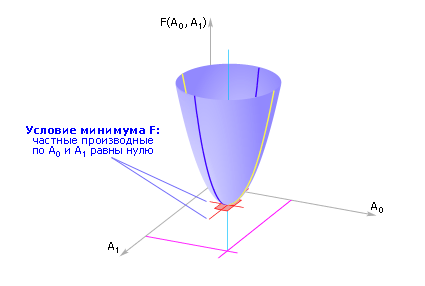уммарная ошибка F является функцией двух переменных A₀ и A₁, то есть F(A₀, A₁), меняя которые, можно влиять на величину суммарной ошибки (см. рис. ниже).

Рис. Примерный вид функции ошибки

Чтобы суммарную ошибку минимизировать, найдем частные производные от функции F по каждой переменной и приравняем их к нулю (условие экстремума):

После раскрытия скобок получим систему из двух линейных уравнений:

Для нахождения коэффициентов A₀ и A₁ методом Крамера представим систему в матричной форме:

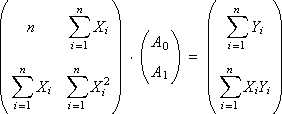
Решение имеет вид:

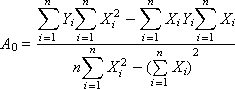
Вычисляем значения A₀ и A₁.

Приклад. Розрахуємо коефіцієнти A₀ та A₁ за допомогою електронної таблиці Excel.

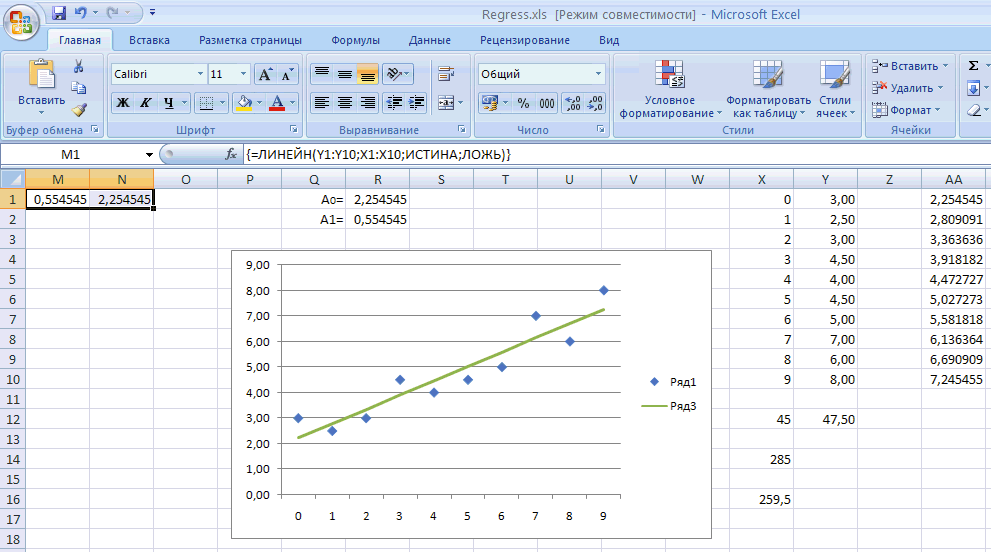
Вихідні дані – по 10 значень X_i та Y_i запишемо у стовпчики відповідно X та Y.

Рішення виконаємо у вигляді ланцюжку простих формул, проміжні значення будемо записувати у окремих комірках електронної таблиці. У комірках X12 та Y12 запишемо суми стовпчиків X1:X10 та Y1:Y10. Суму квадратів значень X_i запишемо у комірку X14 як функцію X14 =СУММКВ(X1:X10). Суму добутків ΣX_iY_i запишемо у комірку X16 у такий спосіб: X16 =СУММПРОИЗВ(X1:X10;Y1:Y10).

Значення A₀ запишемо у комірку R1=(Y12*X14-X16*X12)/(10*X14-X12*X12),

значення A₁ запишемо у комірку R2=(10*X16-Y12*X12)/(10*X14-X12*X12).

Тут необхідно зауважити, що для розрахунків коефіцієнтів лінійної регресії можна скористатися функцією Excel ЛИНЕЙН. Для порівняння, комірки M1 та N1 обчислюються за допомогою такої функції. Як бачимо, результати тотожні значенням R1 та R2.

Запишемо у стовпчик AA1:AA10 значення функції A₀ + A₁X, яку в таблиці обчислимо як

AA1:AA10=R1+R2*(X1:X10)

Відобразимо на діаграмі первісні значення (значення стовпчика Y1:Y10) окремими точками-маркерами, а результат лінійної апроксимації (стовпчик AA1:AA10) суцільною лінією.

Проверка

Чтобы определить, принимается гипотеза или нет, нужно, во-первых, рассчитать ошибку между точками заданной экспериментальной и полученной теоретической зависимости и суммарную ошибку:

E_i = (Y_i^Эксп. – Y_i^Теор.), i = 1, …, n

И, во-вторых, необходимо найти значение σ по формуле , где F — суммарная ошибка, n — общее число экспериментальных точек.

Если в полосу, ограниченную линиями Y^Теор. – S и Y^Теор. + S (рис. 2.5), попадает 68.26% и более экспериментальных точек Y_i^Эксп., то выдвинутая нами гипотеза принимается. В противном случае выбирают более сложную гипотезу или проверяют исходные данные. Если требуется большая уверенность в результате, то используют дополнительное условие: в полосу, ограниченную линиями Y^Теор. – 2S и Y^Теор. + 2S, должны попасть 95.44% и более экспериментальных точек Y_i^Эксп..

Рис. Исследование приемлемости линейной гипотезы

Расстояние S связано с σ следующим соотношением:

S = σ/sin(β) = σ/sin(90° – arctg(A₁)) = σ/cos(arctg(A₁)),

ч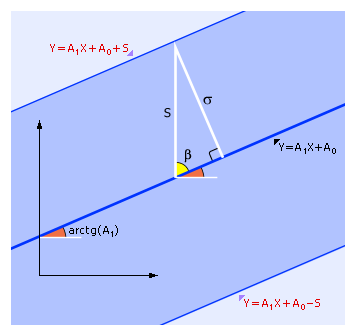то проиллюстрировано на рисунке ниже.

Рис. Связь значений σ и S

У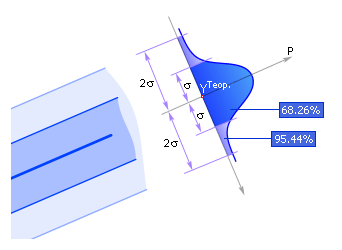словие принятия гипотезы выведено из нормального закона распределения случайных ошибок. P — вероятность распределения нормальной ошибки.

Рис. Иллюстрация закона нормального распределения ошибок

Линейная множественная модель

Здесь количество входных сигналов, действующих одновременно на объект, равно m (см. рис. ниже):

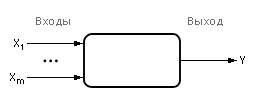
Рис. Обозначение многомерного черного ящика с одним выходом

Предположим, что зависимость значений на выходе линейна относительно входов:

Y = A₀ + A₁ · X₁ + … + A_m · X_m.

Вычисление коэффициентов A₀ , A₁ , …  A_m  произведем способом, аналогичным рассмотренному выше для одномерного варианта. 

Так как подразумевается, что мы имеем экспериментальные данные о всех входах и выходах черного ящика, то можно вычислить ошибку между экспериментальным (Y_i^Эксп.) и теоретическим (Y_i^Теор.) значением Y для каждой i-ой точки (пусть, как и прежде, число экспериментальных точек равно n):

E_i = (Y_i^Эксп. – Y_i^Теор.), i = 1, …, n;

E_i = Y_i – A₀ – A₁ · X_1i – … – A_m · X_mi, i = 1, …, n.

Минимизируем суммарную ошибку F:

Ошибка F зависит от выбора параметров A₀, A₁, …, A_m. Для нахождения экстремума приравняем все частные производные F по неизвестным A₀, A₁, …, A_m к нулю:

Получим систему из m + 1 уравнения с m + 1 неизвестными, которую следует решить, чтобы определить коэффициенты линейной множественной модели A₀, A₁, …, A_m. Для нахождения искомых коэффициентов представим систему в матричном виде:

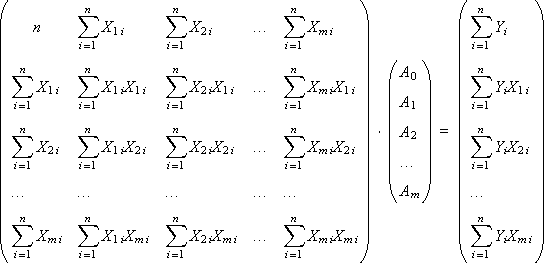
Вычисляем коэффициенты A₀, A₁, …, A_m решением данной системы линейных уравнений.

Далее, как и для одномерной модели, для каждой точки вычисляется ошибка E_i; затем находится суммарная ошибка F и значения σ и S с целью определить, принимается ли выдвинутая гипотеза о линейности многомерного черного ящика или нет.

При помощи подстановок и переобозначений к линейной множественной модели приводятся многие нелинейные модели.

Розглянемо приклад розрахунків коефіцієнтів лінійної множинної регресії (m=2, n=10).

Значення X_1i, X_2i та Y_i надані у таблиці.

Y	X1	X2
22,1	0	4
22,8	2	3
48,5	4	7
22,8	5	1
30,6	6	2
38,1	7	3
46	8	4
44,2	9	3
38	10	1
61	11	5

Необхідно обчислити коефіцієнти A₀, A₁ и A₂ лінійної регресії Y = A₀ + A₁ X₁ + A₂X₂ а також значення σ.

Рішення у середовищі електронної таблиці Excel.

Записуємо значення X_1i, X_2i та Y_i у стовпчики відповідно (A1:A10), (B1:B10) та (C1:C10).

У комірки (E1:G3) записуємо матрицю системи рівнянь, у (I1:I3) – стовпчик правої частини рівнянь (вільні члени).

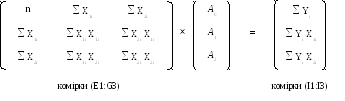
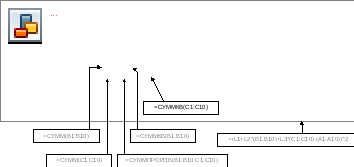
Рішення системи рівнянь виконуємо методом зворотної матриці. Знаходимо зворотну матрицю й далі її множимо на стовпчик вільних членів. Для цього у комірки L1:L3 записуємо формулу =МУМНОЖ(МОБР(E1:G3);I1:I3)

Розраховані значення коефіцієнтів A₀, A₁ и A₂ містяться у стовпчику L1:L3.

Таким чином, рівняння множинної регресії має вигляд:

Y = 2.335096798 + 3.073691099 X₁ + 4.853944965 X₂

Для розрахунку σ у комірку L4 записуємо функцію =КОРЕНЬ(СУММ(O1:O10)/10)