
- •Интегралы, зависящие от параметра
- •§1. Собственные интегралы, зависящие от параметра
- •1. Определение интегралов, зависящих от параметра
- •2. Равномерная сходимость по параметру семейства функций
- •3. Предельный переход под знаком интеграла
- •4 Непрерывность по параметру
- •5. Дифференцирование по параметру
- •6. Интегрирование по параметру
- •§2. Несобственные интегралы, зависящие от параметра
- •1. Равномерная сходимость интегралов
- •2. Свойства несобственных интегралов, зависящих от параметра
- •§3. Интегралы Эйлера
- •Интеграл Эйлера первого рода (Бета-функция)
- •Интеграл Эйлера второго рода (Гамма-функция)
3. Предельный переход под знаком интеграла
Пусть y0-
предельная точка множества Y.
Поставим вопрос о пределе функции (2)
при yy0:
![]() -?
-?
Теорема 4.
Если функция f(x;y)
при фиксированном y
непрерывна по х
в [a;b]
и при yy0
стремится к предельной функции (х)
 равномерно относительно х,
то имеет место равенство:
равномерно относительно х,
то имеет место равенство:
 . (4)
. (4)
Доказательство.
![]() По теореме 3
функция (х)
непрерывна на [a;b].
Следовательно,
По теореме 3
функция (х)
непрерывна на [a;b].
Следовательно,
 .
По условию f(x;y)
непрерывна по х
на [a;b],
следовательно, она интегрируема по х
на [a;b],
т.е.
.
По условию f(x;y)
непрерывна по х
на [a;b],
следовательно, она интегрируема по х
на [a;b],
т.е.
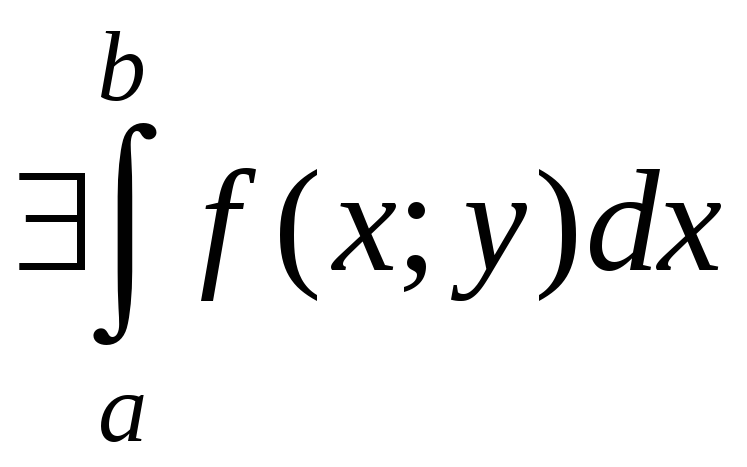 .
.
Т.к.
![]() при yy0,
то по определению >0
>0:
y:
| y-y0|<,
xX
выполнено
при yy0,
то по определению >0
>0:
y:
| y-y0|<,
xX
выполнено![]() .
Оценим модуль разности:
.
Оценим модуль разности:
 .
.
Итак, >0
>0:
yY:
| y-y0|<
выполнено .
По определению это значит, что
.
По определению это значит, что
 .
.
![]()
Формула (4) может быть записана в виде:
 .
.
В этом случае говорят, что возможен предельный переход по параметру под знаком интеграла.
4 Непрерывность по параметру
I.
Случай
интеграла (2):
 .
.
Пусть Y=[c;d]. Решим вопрос о непрерывности функции (2).
Теорема 5. Если функция f(x;y) определена и непрерывна как функция двух переменных в прямоугольнике [a,b;c,d], то интеграл (2) будет непрерывной функцией параметра y на отрезке [c;d].
Доказательство.
![]() Т.к. f(x;y)
непрерывна на замкнутом множестве
[a,b;c,d],
то она равномерно непрерывна на этом
множестве. По определению
Т.к. f(x;y)
непрерывна на замкнутом множестве
[a,b;c,d],
то она равномерно непрерывна на этом
множестве. По определению
![]() выполнено
выполнено
![]() .
.
Положим
![]() ,
тогда при
,
тогда при
![]() выполнено
выполнено
![]() .
Согласно определению функция f(x;y)
при yy0
стремится равномерно к функции
.
Согласно определению функция f(x;y)
при yy0
стремится равномерно к функции
![]() .
Тогда по теореме 4
.
Тогда по теореме 4
 или
или
![]() .
По определению I(y)
непрерывна y0[c;d],
т.е. на непрерывна [c;d].
.
По определению I(y)
непрерывна y0[c;d],
т.е. на непрерывна [c;d].
![]()
II.
Случай
интеграла (1):
 .
.
Теорема 6.
Если
функция f(x;y)
непрерывна в замкнутой области
![]() ,
функции (y)
и (y)
непрерывны на [c;d],
то функция (1) непрерывна на [c;d].
,
функции (y)
и (y)
непрерывны на [c;d],
то функция (1) непрерывна на [c;d].
Доказательство.
![]() Зафиксируем
y0[c;d].
Тогда (1) можно записать в виде:
Зафиксируем
y0[c;d].
Тогда (1) можно записать в виде:

 .
.
В первом интеграле
 пределы интегрирования постоянны (не
зависят от параметра). Следовательно,
по теореме 5, при yy0
этот интеграл стремится к
пределы интегрирования постоянны (не
зависят от параметра). Следовательно,
по теореме 5, при yy0
этот интеграл стремится к
 .
.
Оценим остальные два интеграла:
 ,
,  ,
,
где
![]() .
Т.к. функции (y)
и (y)
непрерывны, то при yy0
(y)(y0),
(y)(y0),
следовательно, |(y)-(y0)|0,
|(y)-(y0)|0,
значит, два последних интеграла стремятся
к нулю при yy0.
Тогда
.
Т.к. функции (y)
и (y)
непрерывны, то при yy0
(y)(y0),
(y)(y0),
следовательно, |(y)-(y0)|0,
|(y)-(y0)|0,
значит, два последних интеграла стремятся
к нулю при yy0.
Тогда
![]() .
По определению I(y)
непрерывна y0[c;d],
т.е. непрерывна на [c;d].
.
По определению I(y)
непрерывна y0[c;d],
т.е. непрерывна на [c;d].
![]()
Замечание 1. В силу непрерывности функций (y), (y), f(x;y) утверждение теоремы 6 можно записать в виде:
 .
.
Замечание 2. Утверждения теорем 5 и 6 доказаны в теории двойных интегралов.
5. Дифференцирование по параметру
I.
Случай
интеграла (2):
 .
.
Теорема
7 (правило Лейбница).
Пусть функция f(x;y)
определена в прямоугольнике [a,b;c,d],
непрерывна по х
на [a;b]
при любом фиксированном значении
y[c;d].
Пусть, далее, во всей области существует
частная производная
![]() ,
непрерывная как функция двух переменных.
Тогда функция I(y)
дифференцируема на [c;d]
и справедлива формула:
,
непрерывная как функция двух переменных.
Тогда функция I(y)
дифференцируема на [c;d]
и справедлива формула:
 . (6)
. (6)
Доказательство.
![]() Т.к. f(x;y)
непрерывна по х
y[c;d],
то интеграл (2) определен. Фиксируем
y=y0[c;d].
Придадим ему приращение y0:
y+y[c;d].
Тогда функция I(y)
получит приращение:
Т.к. f(x;y)
непрерывна по х
y[c;d],
то интеграл (2) определен. Фиксируем
y=y0[c;d].
Придадим ему приращение y0:
y+y[c;d].
Тогда функция I(y)
получит приращение:

 .
.
Т.к. функция f(x;y) непрерывна на отрезке [c;d] и дифференцируема по y, то применим к ней формулу Лагранжа:
![]() . (7)
. (7)
Тогда
 . (8)
. (8)
Т.к. функция
![]() непрерывна на замкнутом прямоугольнике
[a,b;c,d],
то она равномерно непрерывна на нем. По
определению
непрерывна на замкнутом прямоугольнике
[a,b;c,d],
то она равномерно непрерывна на нем. По
определению
![]() выполнено
выполнено
![]() .
.
Полагая
![]() и считая
и считая
![]() ,
получим:
,
получим:
![]() выполнено
выполнено
![]() .
.
По определению
функция
![]() равномерно стремится к функции
равномерно стремится к функции
![]() на [a;b]
при y
0.
Кроме того, функция
на [a;b]
при y
0.
Кроме того, функция
![]() непрерывна по х
на [a;b]
(т.к. непрерывна как функция двух
переменных на [a,b;c,d]),
следовательно, по теореме 4 допустим
предельный переход под знаком интеграла:
непрерывна по х
на [a;b]
(т.к. непрерывна как функция двух
переменных на [a,b;c,d]),
следовательно, по теореме 4 допустим
предельный переход под знаком интеграла:
 .
.
Итак
![]() правой
части равенства (8) следовательно,
правой
части равенства (8) следовательно,
![]()
![]() левой части равенства (8):
левой части равенства (8):
 .
Переходя в равенстве (8) к пределу при
y
0,
получим
.
Переходя в равенстве (8) к пределу при
y
0,
получим
 .
Т.к y0
– произвольная точка из отрезка [c;d],
то равенство теорема доказана.
.
Т.к y0
– произвольная точка из отрезка [c;d],
то равенство теорема доказана.
![]()
II.
Случай
интеграла (1):
 .
.
Теорема 8. Пусть:
-
функция f(x;y) и её частная производная
 непрерывны на замкнутом промежутке
=[a,b;c,d],
непрерывны на замкнутом промежутке
=[a,b;c,d], -
 ,
, -
Функции (y) и (y) имеют непрерывные производные на [c;d].
Тогда интеграл (1) имеет производную на [c;d], причем
 . (9)
. (9)
Доказательство.
![]() Рассмотрим
функцию
Рассмотрим
функцию
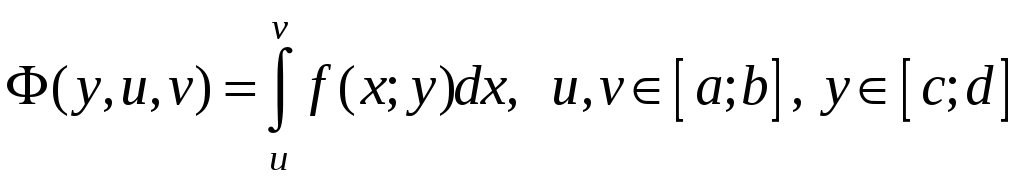 ,
из которой I(y)
получается подстановкой u=(y),
v=(y).
Таким образом, вопрос дифференцирования
функции I(y)
исчерпывается применением теорем о
непрерывности и дифференцировании
сложной функции. Покажем, что
,
из которой I(y)
получается подстановкой u=(y),
v=(y).
Таким образом, вопрос дифференцирования
функции I(y)
исчерпывается применением теорем о
непрерывности и дифференцировании
сложной функции. Покажем, что
![]() функции (y;u;v)
существуют и непрерывны по совокупности
переменных
y,
u,
v.
функции (y;u;v)
существуют и непрерывны по совокупности
переменных
y,
u,
v.
1) Проверим
существование и непрерывность частной
производной
![]() .
Её существование следует из теоремы 7,
причем
.
Её существование следует из теоремы 7,
причем
 .
.
Докажем её непрерывность.
Пусть u,v[a;b], u+u[a;b], v+v[a;b], y[c;d]. y+y[c;d]
![]() ,
,



 .
.
Т.к.
![]() определена на ,
то в силу выбора значений аргументов
все написанные интегралы имеют смысл
и |v-y||b-a|.
определена на ,
то в силу выбора значений аргументов
все написанные интегралы имеют смысл
и |v-y||b-a|.
Т.к.
![]() непрерывна на ,то
она ограничена на нем, т.е.
непрерывна на ,то
она ограничена на нем, т.е.
![]() .
.
Тогда  ,
,  .
.
Оценим первое
слагаемое. В процессе доказательства
теоремы 7 было показано, что
![]() .
По определению
.
По определению
![]() выполнено
выполнено
![]() ,
,
или (что тоже самое)
![]() .
Итак,
.
Итак,
![]() при
при
![]() .
Следовательно,
.
Следовательно,
![]() .
По определению
.
По определению
![]() непрерывна на множестве
непрерывна на множестве
![]() .
.
2) Проверим
существование и непрерывность
![]() :
:
 ,
,  .
.
f(v;y), -f(u;y) - непрерывны на 1 по теореме о непрерывности сложной функции.
3) Связь между
функциями I
и Ф устанавливается формулой:
![]() .
В силу доказанного выше функцию I(y)
можно дифференцировать по правилу
дифференцирования сложной функции:
.
В силу доказанного выше функцию I(y)
можно дифференцировать по правилу
дифференцирования сложной функции:
![]() .
Следовательно,
.
Следовательно,
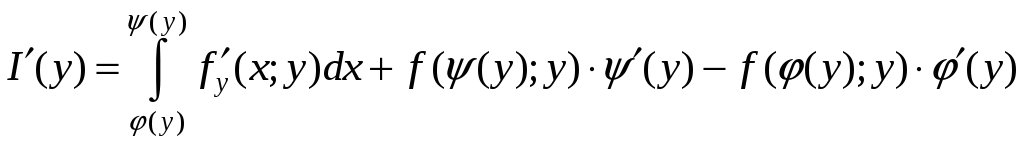 .
.
![]()
