
- •Интегралы, зависящие от параметра
- •§1. Собственные интегралы, зависящие от параметра
- •1. Определение интегралов, зависящих от параметра
- •2. Равномерная сходимость по параметру семейства функций
- •3. Предельный переход под знаком интеграла
- •4 Непрерывность по параметру
- •5. Дифференцирование по параметру
- •6. Интегрирование по параметру
- •§2. Несобственные интегралы, зависящие от параметра
- •1. Равномерная сходимость интегралов
- •2. Свойства несобственных интегралов, зависящих от параметра
- •§3. Интегралы Эйлера
- •Интеграл Эйлера первого рода (Бета-функция)
- •Интеграл Эйлера второго рода (Гамма-функция)
-
Интеграл Эйлера второго рода (Гамма-функция)
Определение. Интегралом Эйлера второго рода (Гамма-функцией) называется интеграл вида
 .
(5)
.
(5)
Покажем, что этот интеграл сходится при a>0. Для этого представим его в виде:
 .
.
Интеграл I1
является собственным при a1
и несобственным при a<1
(особая точка х=0).
Подынтегральная функция
 .
Положим
.
Положим
![]() .
Т.к.
.
Т.к.
 (конечный, 0),
то интегралы
(конечный, 0),
то интегралы
 и
и
 сходятся или расходятся одновременно.
Следовательно, I1
сходится при 1-a<1
или a>0.
сходятся или расходятся одновременно.
Следовательно, I1
сходится при 1-a<1
или a>0.
Рассмотрим I2.
Т.к. при любом a
 ,
то k>1:
xk
будет, например, выполнено
,
то k>1:
xk
будет, например, выполнено
 .
Разделив обе части неравенства на х2
(х2k2>1),
получим
.
Разделив обе части неравенства на х2
(х2k2>1),
получим
 a.
Т.к.
a.
Т.к.
![]() сходится, то сходится и
сходится, то сходится и
 a,
а, значит, при любом a
сходится и
a,
а, значит, при любом a
сходится и
 .
.
Следовательно, интеграл (5) сходится, если a>0 и расходится, если a0.
Т.е. областью определения функции (a) является промежуток (0;+).
Свойства Гамма-функции
1. (a)>0, a(0;+).
Это следует из выражения (5) для Гамма-функции.
2. Гамма-функция при всех a>0 непрерывна и имеет непрерывные производные всех порядков, причем
 . (6)
. (6)
![]() Установим существование первой
производной и равенство
Установим существование первой
производной и равенство
 .
.
Возьмем a0>0. Всегда можно указать промежуток [c;d] (0<c<d<+), такой, что c<a0<d. Имеем
1)
![]() и
и
![]() непрерывны в области
непрерывны в области
![]() .
.
2)
 сходится в промежутке [c;d].
сходится в промежутке [c;d].
3) Покажем, что
 сходится равномерно относительно a
на промежутке [c;d].
сходится равномерно относительно a
на промежутке [c;d].
Имеем
 .
.
Рассмотрим
 .
.
Т.к. 0<x1,
cad,
то
![]() .
Учитывая, что lnx0,
получим
.
Учитывая, что lnx0,
получим
![]() .
Тогда
.
Тогда
![]() .
.
Т.к. e-x<1
при x(0;1],
то
![]() .
Интегрируя по частям, получим
.
Интегрируя по частям, получим
 .
.
Известно, что
![]() сходится при 1-c<1,
т.е. при c>0.
Следовательно, по признаку Вейерштрасса
равномерной сходимости несобственных
интегралов, зависящих от параметра,
заключаем, что
сходится при 1-c<1,
т.е. при c>0.
Следовательно, по признаку Вейерштрасса
равномерной сходимости несобственных
интегралов, зависящих от параметра,
заключаем, что
 сходится равномерно относительно
параметра a
на промежутке [c;d].
сходится равномерно относительно
параметра a
на промежутке [c;d].
Рассмотрим
 .
.
При x1,
cad,
выполнено
![]() .
Т.к. lnx0,
получим
.
Т.к. lnx0,
получим
![]() .
Имеем
.
Имеем
![]() .
Т.к.
.
Т.к.
![]() ,
то существует точка
,
то существует точка
![]() ,
такая, что для
,
такая, что для
![]() будет
будет
![]() .
Следовательно, для
.
Следовательно, для
![]() :
:
![]() .
Т.к.
.
Т.к.
 сходится при любом конечном d,
то сходится
сходится при любом конечном d,
то сходится
 ,
а, значит, и
,
а, значит, и
 .
А тогда по признаку Вейерштрасса
равномерной сходимости несобственных
интегралов, зависящих от параметра,
заключаем, что
.
А тогда по признаку Вейерштрасса
равномерной сходимости несобственных
интегралов, зависящих от параметра,
заключаем, что
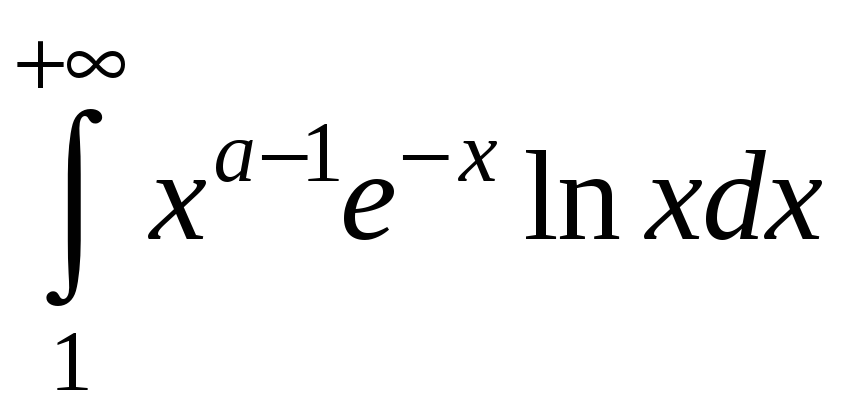 сходится равномерно относительно
параметра a
на промежутке [c;d].
сходится равномерно относительно
параметра a
на промежутке [c;d].
Т.о., окончательно
приходим к выводу, что
 сходится равномерно относительно
параметра a
на промежутке [c;d].
сходится равномерно относительно
параметра a
на промежутке [c;d].
Значит,
![]() существует
a[c;d],
в частности,
существует
a[c;d],
в частности,
![]() .
Т.к. a0>0
– произвольная точка, то
.
Т.к. a0>0
– произвольная точка, то
![]() существует для a(0;+),
причем
существует для a(0;+),
причем
 .
.
Доказательство
равенства (6) проводится по индукции.
![]()
3. Применяя формулу интегрирования по частям, находим
 .
.
Отсюда
a(a)=(a+1). (7)
Это равенство выражает основное свойство Гамма-функции.
Из (7) при
![]() и 0<a<1
получим
и 0<a<1
получим
(n+a)=(n+a-1)(n+a-1)=(n+a-1)(n+a-2)(n+a-2)=…=
=(n+a-1)(n+a-2)(n+a-3)…a(a). (8)
Т.о., значение Гамма-функции от аргумента n+a>1 можно выразить через значение аргумента a<1. Поэтому таблица значений Гамма-функции обычно дается для значений аргумента из интервала (0;1).
В частности, если в формуле (8) положить a=1 и учесть, что
 ,
,
То получим
(n+1)=n(n-1)(n-2)…21=n!
Т.о., Гамма-функцию
можно считать обобщением факториала
натурального числа: Гамма-функция
является продолжением функции a!,
определенной только для
![]() на всю полуось a>0
действительных чисел.
на всю полуось a>0
действительных чисел.
4.
а)
![]() ;
б)
;
б)
![]() .
.
![]() а)
Т.к.
а)
Т.к.
![]() a>n,
то
a>n,
то
![]() .
.
б) Запишем
соотношение (7) в виде
 и перейдем к пределу при a+0.
В силу непрерывности Гамма-функции в
интервале (0;+)
и перейдем к пределу при a+0.
В силу непрерывности Гамма-функции в
интервале (0;+)
![]() .
Значит, и
.
Значит, и
 .
Следовательно,
.
Следовательно,
![]() .
Т.е при приближении к нулю справа
гамма-функция ведет себя, как положительная
бесконечно большая величина
.
Т.е при приближении к нулю справа
гамма-функция ведет себя, как положительная
бесконечно большая величина
![]() .
.
![]()
5. Покажем, что между Бета-функцией и Гамма-функцией существует следующая связь:
 . (9)
. (9)
![]() Сделаем в интеграле
Сделаем в интеграле
 замену переменной: x=(1+u)t
(t>0)
замену переменной: x=(1+u)t
(t>0)
 .
.
Отсюда  .
.
Умножим
обе части этого равенства на
![]() и
проинтегрируем по u
от 0 до +:
и
проинтегрируем по u
от 0 до +:
 .
.
Т.к.
 ,
то последнее неравенство запишем в
виде:
,
то последнее неравенство запишем в
виде:
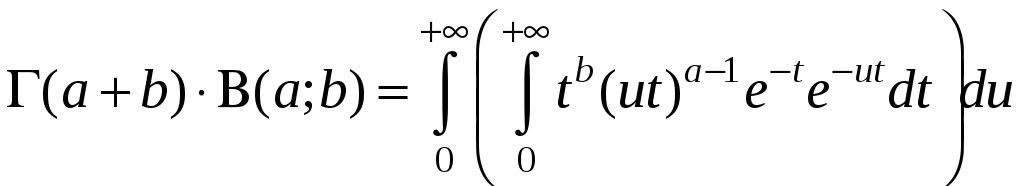 .
.
В интеграле в правой части поменяем порядок интегрирования:
 .
.
Во внутреннем интеграле сделаем замену v=ut:
 .
.
Отсюда получаем
(9).
![]()
В частности,
![]() .
Если 0<a<1,
то отсюда
.
Если 0<a<1,
то отсюда
![]() . (10)
. (10)
Формула (10) называется формулой дополнения.
Полагая
![]() ,
отсюда получим:
,
отсюда получим:
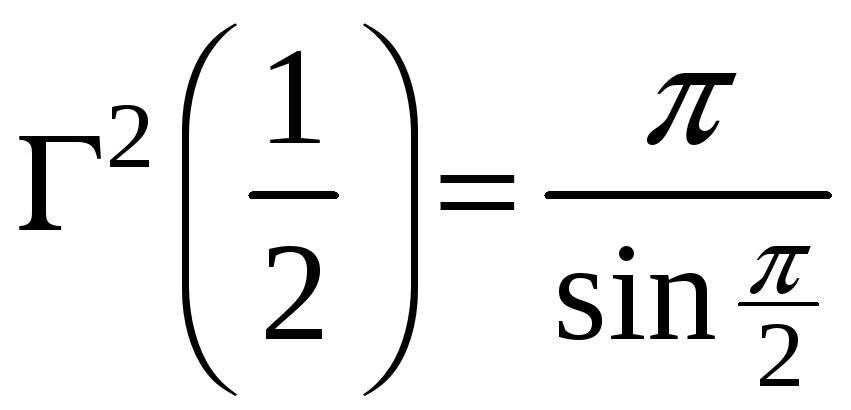 ,
следовательно,
,
следовательно,
 . (11)
. (11)
Из соотношений (8), (11), получим
 ,
,
т.е. 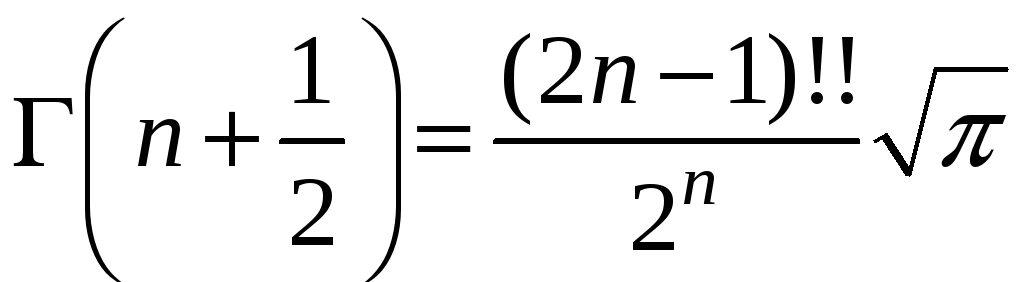 .
.
С помощью соотношения (11) можно вычислить интеграл Пуассона.
 ,
,

 .
.
Замечание 1. При выводе формулы (9) мы переставили два интеграла с бесконечными пределами, зависящих от параметра. Теорема 7 обосновывает перестановку двух интегралов, из которых лишь один распространен на бесконечный промежуток. Доказательство возможности перестановки двух интегралов с бесконечными пределами можно найти в учебнике Л.Д. Кудрявцева «Курс математического анализа», т.2.
Замечание 2. Гамма-функция, не являющаяся элементарной, играет в математике важную роль. Для функции Г(а) составлены подробные таблицы, и при вычислениях она может использоваться наряду с простейшими элементарными функциями – показательной, тригонометрическими и т.д.
Оказывается, что определенные интегралы различных типов могут быть выражены через Гамма-функцию. В частности, к таким интегралам нередко приводят задачи, связанные с вычислением площадей и объемов. Даже если функция имеет первообразную, являющуюся элементарной функцией, интеграл зачастую целесообразно вычислять, используя Гамма-функцию.
