
- •Интегралы, зависящие от параметра
- •§1. Собственные интегралы, зависящие от параметра
- •1. Определение интегралов, зависящих от параметра
- •2. Равномерная сходимость по параметру семейства функций
- •3. Предельный переход под знаком интеграла
- •4 Непрерывность по параметру
- •5. Дифференцирование по параметру
- •6. Интегрирование по параметру
- •§2. Несобственные интегралы, зависящие от параметра
- •1. Равномерная сходимость интегралов
- •2. Свойства несобственных интегралов, зависящих от параметра
- •§3. Интегралы Эйлера
- •Интеграл Эйлера первого рода (Бета-функция)
- •Интеграл Эйлера второго рода (Гамма-функция)
2. Свойства несобственных интегралов, зависящих от параметра
а) Предельный переход под знаком интеграла
Теорема 5. Пусть функция f(x;y) определена для xa и yY. Если:
-
f(x;y) непрерывна по х;
-
f(x;y) при yy0 стремится к предельной функции (x) равномерно относительно х в каждом конечном промежутке [a;A];
-
интеграл (1) сходится равномерно относительно у в области Y,
то  . (8)
. (8)
Доказательство.
![]() 1) Функция
(x)-непрерывна
(в силу условий теоремы).
1) Функция
(x)-непрерывна
(в силу условий теоремы).
2) из (3) следует
>0
A0a:
A>A>A0,
yY
выполнено
 .
.
Переходя в последнем
неравенстве к пределу при yy0
(это возможно сделать по теореме о
предельном переходе в собственном
интеграле на основании условия), получим
 .
Следовательно, функция (x)
интегрируема на [a;+),
т.е.
.
Следовательно, функция (x)
интегрируема на [a;+),
т.е.
 .
.
3) A>a имеем
 . (9)
. (9)
По определению 2
из п.1  . (10)
. (10)
Из существования
 следует
следует  . (11)
. (11)
Из п.2 следует, что для сколь угодно большого А
 .(12)
.(12)
Из (9)-(12) следует: .
.
По определению
это означает, что выполнено (8).
![]()
б) Непрерывность несобственного интеграла
Теорема 6. Пусть функция f(x;y) определена и непрерывна как функция двух переменных для значений xa и y[c;d]. Если интеграл (1) сходится равномерно относительно у в промежутке [c;d], то он представляет собой непрерывную функцию от параметра у в этом промежутке.
Доказательство.
![]() Пусть
x[a;A],
yy0,
y0[c;d].
В теореме
5 §1 (п.4) показано, что функция f(x;y)
в этом случае равномерно относительно
х
стремится к предельной функции f(x;y0).
Тогда по этой теореме в интеграле (1)
можно перейти к пределу под знаком
интеграла:
Пусть
x[a;A],
yy0,
y0[c;d].
В теореме
5 §1 (п.4) показано, что функция f(x;y)
в этом случае равномерно относительно
х
стремится к предельной функции f(x;y0).
Тогда по этой теореме в интеграле (1)
можно перейти к пределу под знаком
интеграла:
 .
.
По определению
I(y)
непрерывна в точке y=y0,
а следовательно, и на [c;d].
![]()
в) Интегрирование по параметру
Теорема 7. При предположениях теоремы 6 имеет место равенство:
 .
.
Доказательство.
![]() Возьмем A>a.
Тогда
Возьмем A>a.
Тогда
 . (13)
. (13)
По теореме 9 §1:
 .
Поэтому из (13) получим
.
Поэтому из (13) получим
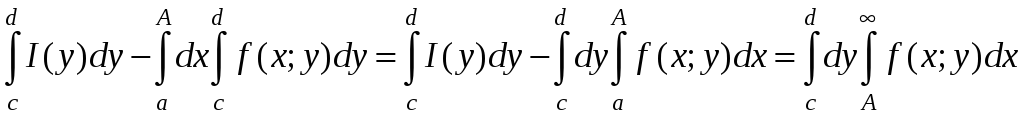 .
.
В силу равномерной
сходимости интеграла (1) >0
A0a:
A>A0,
y[c;d]
выполнено
 .
.
Тогда
 .
.
По определению
 ,
т. е.
,
т. е.
 .
.![]()
г) Дифференцирование по параметру
Теорема 8. Пусть функция f(x;y) определена и непрерывна по х для xa и y[c;d]. Если:
1) f(x;y)
имеет непрерывную производную
![]() по обеим переменным для xa
и y[c;d];
по обеим переменным для xa
и y[c;d];
2) интеграл (1) сходится y[c;d];
3) интеграл
 сходится равномерно по y[c;d],
сходится равномерно по y[c;d],
то y[c;d]
имеет место формула:
 .
.
Доказательство.
![]() К функции
К функции
![]() на отрезке [c;y],
y[c;d]
применим теорему 7:
на отрезке [c;y],
y[c;d]
применим теорему 7:

 .
.
Так как функция
 непрерывна по у
(по теореме 6), то по свойству интеграла
с переменным верхним пределом
непрерывна по у
(по теореме 6), то по свойству интеграла
с переменным верхним пределом

 .
Тогда
.
Тогда
 ,
т.е.
,
т.е.
 .
.
![]()
§3. Интегралы Эйлера
-
Интеграл Эйлера первого рода (Бета-функция)
Определение. Интегралом Эйлера первого рода (Бета-функцией) называется интеграл вида
 .
(1)
.
(1)
Этот интеграл является собственным, если одновременно a1, b1. Если же хотя бы одно из этих условий не выполнено, то он – несобственный.
Покажем, что интеграл (1) сходится. Если одновременно a>0, b>0.
Подынтегральная функция имеет, вообще говоря, две особые точки: х=0 и х=1. Поэтому представим (1) в виде:
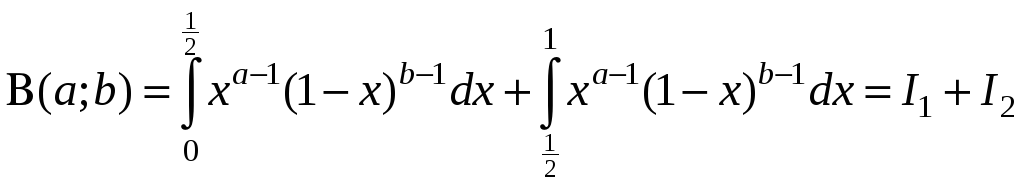 .
.
Интеграл I1
является несобственным при a<1,
особая точка х=0.
Запишем подынтегральную функцию в виде
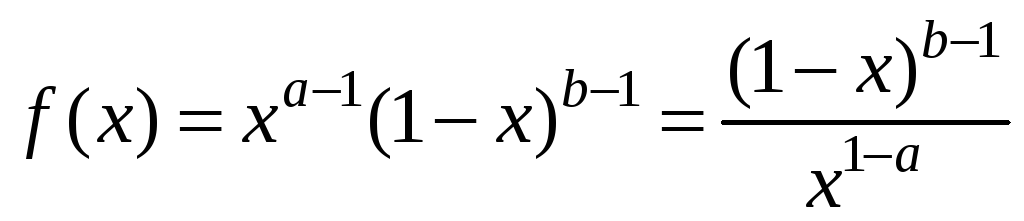 и введем функцию
и введем функцию
![]() .
Т.к.
.
Т.к.
 при любом b
(конечный, 0),
то интегралы
при любом b
(конечный, 0),
то интегралы
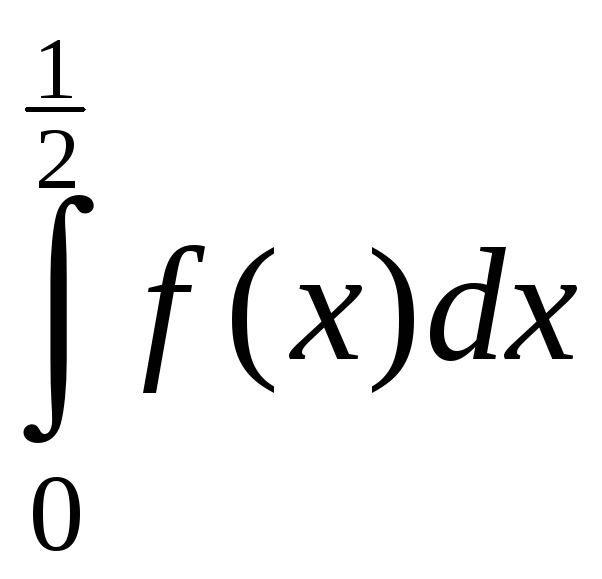 и
и
 сходятся или расходятся одновременно.
Но
сходятся или расходятся одновременно.
Но
 сходится при 1-a<1,
т.е. a>0.
Следовательно, I1
сходится при любом b
и a>0.
сходится при 1-a<1,
т.е. a>0.
Следовательно, I1
сходится при любом b
и a>0.
Рассмотрим I2.
Он является несобственным при b<1,
особая точка х=1.
Подынтегральная функция
 .
Положим
.
Положим
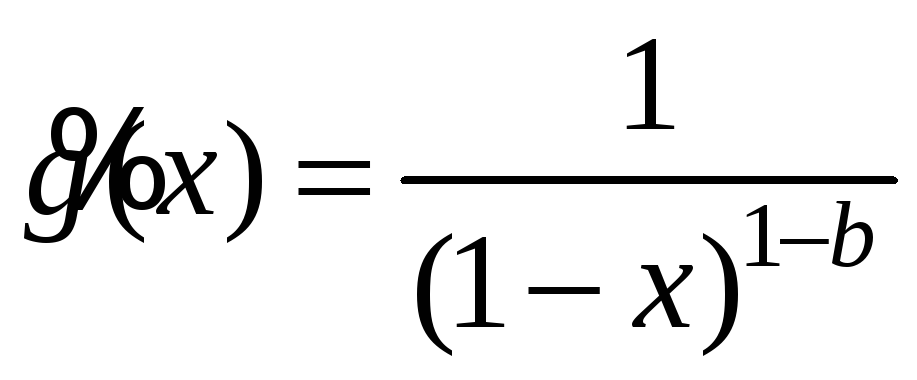 .
Т.к.
.
Т.к.
 при любом a
(конечный, 0),
то интегралы
при любом a
(конечный, 0),
то интегралы
 и
и
 сходятся или расходятся одновременно.
Т.к.
сходятся или расходятся одновременно.
Т.к.
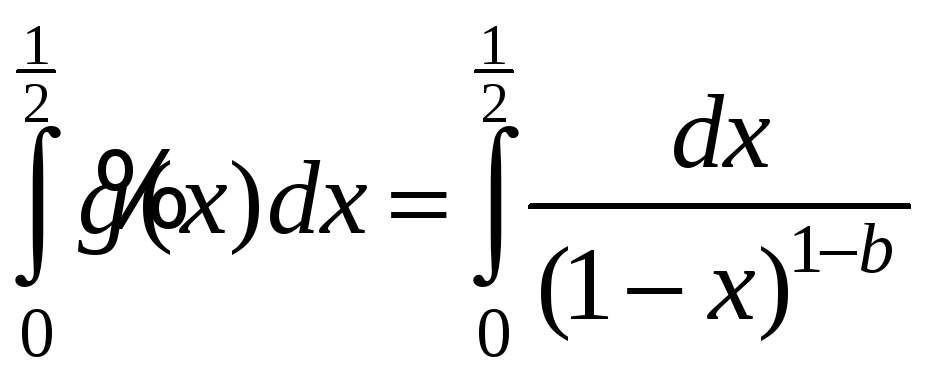 сходится при 1-b<1,
т.е. b>0,
то I2
сходится при любом a
и b>0.
сходится при 1-b<1,
т.е. b>0,
то I2
сходится при любом a
и b>0.
Следовательно, интеграл (1) сходится, если a>0, b>0. Т.е. множество {(a;b)| a>0, b>0} – область определения Бета-функции (a;b).
Свойства Бета-функции
1. Положим в (1) x=1-t, получим:

 , (2)
, (2)
т. е. Бета-функция – симметричная функция.
2. Пусть b>1. Применяя формулу интегрирования по частям, находим
 .Т.к.
.Т.к.
![]() ,
то
,
то
 ,
,
т.е. ![]() .
.
Отсюда ![]() ,
или
,
или
![]() . (3)
. (3)
Т.к. Бета-функция – симметричная, то при a>1 будет справедлива формула:
![]() . (4)
. (4)
Формулы (3) и (4)
можно применять для «уменьшения»
аргументов, чтобы сделать их, например,
меньше 1. Если b=n,
где
![]() ,
то применяя формулу (3) повторно, получим
,
то применяя формулу (3) повторно, получим
![]()
![]() .
.
Но
 .
.
Поэтому  .
.
Если же еще и
![]() ,
то
,
то
 .
.
3.
Получим для Бета-функции другое
аналитическое выражение. Для этого
сделаем в (1) замену переменной:
 .
Тогда
.
Тогда
 ,
,
 .
Получим
.
Получим
 .
.
4. Если b=1-a и 0<a<1 (а значит, и 0<b<1), то из последнего соотношения
 .
.
(указанный интеграл вычислен Эйлером).
Если, в частности,
взять
![]() ,
то
,
то
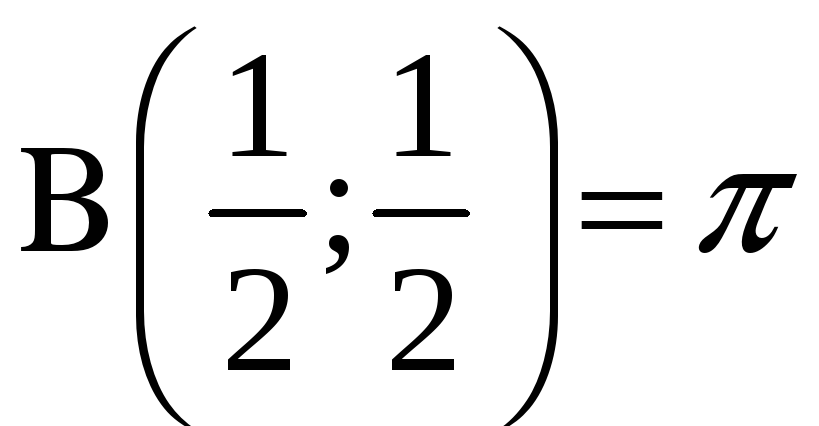 .
.
