
- •Интегралы, зависящие от параметра
- •§1. Собственные интегралы, зависящие от параметра
- •1. Определение интегралов, зависящих от параметра
- •2. Равномерная сходимость по параметру семейства функций
- •3. Предельный переход под знаком интеграла
- •4 Непрерывность по параметру
- •5. Дифференцирование по параметру
- •6. Интегрирование по параметру
- •§2. Несобственные интегралы, зависящие от параметра
- •1. Равномерная сходимость интегралов
- •2. Свойства несобственных интегралов, зависящих от параметра
- •§3. Интегралы Эйлера
- •Интеграл Эйлера первого рода (Бета-функция)
- •Интеграл Эйлера второго рода (Гамма-функция)
6. Интегрирование по параметру
Теорема 9.
Пусть G-простая
область (то есть
![]() ),
где функции (y)
и (y)
непрерывны на [c;d],
а функции 1(x)
и 1(x)
непрерывны на [a;b].
Тогда если функция f(x;y)
непрерывна на замыкании
),
где функции (y)
и (y)
непрерывны на [c;d],
а функции 1(x)
и 1(x)
непрерывны на [a;b].
Тогда если функция f(x;y)
непрерывна на замыкании
![]() области G,
то
области G,
то
 .
.
Теорема 9 является
переформулировкой теоремы о сведении
двойного интеграла к повторному,
доказанной раннее. В частности, для
прямоугольной области [a,b;c,d]
получаем формулу:
 .
.
Говорят, что функцию (2) можно интегрировать по параметру у “под знаком интеграла”.
§2. Несобственные интегралы, зависящие от параметра
1. Равномерная сходимость интегралов
Пусть функция f(x;y) определена xa и yY.
Определение 1. Пусть при каждом y=y0Y существует интеграл
 .
.
Тогда интеграл
 (1)
(1)
называется сходящимся на множестве Y.
По определению несобственного интеграла с бесконечным пределом:
 .
.
Интеграл  (2)
(2)
представляет собой функцию от А и у.
Определение 2. Если стремление интеграла (2) к I(y) происходит равномерно относительно у в области Y, то интеграл I(y) называется равномерно сходящимся относительно у для указанных значений параметра.
Определение 2 означает, что >0 A0a: A>A0, yY выполнено
 .
.
Определение 3. Сходящийся на множестве Y интеграл (1) I(y) называется равномерно сходящимся на этом множестве, если
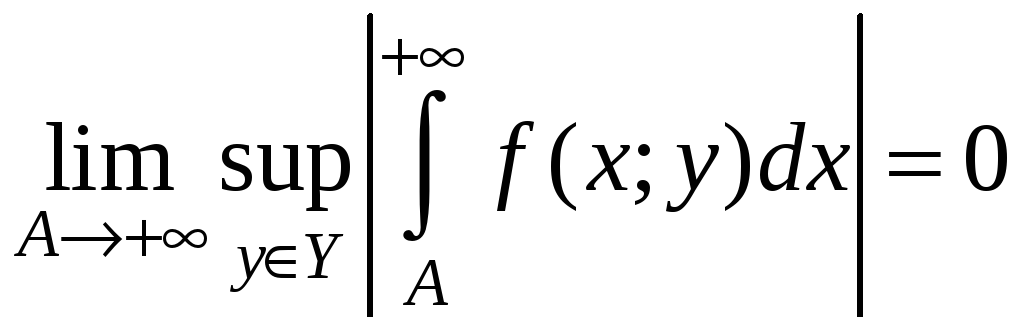 .
.
Определение 2 равносильно определению 3 (доказательство аналогично проведенному в случае собственного интеграла).
Теорема
1
(необходимое и достаточное условие
равномерной сходимости).
Для того
чтобы интеграл (1) сходился равномерно
относительно у
в области Y
необходимо и достаточно, чтобы >0
A0a:
A>A>A0,
yY
выполнялось
 .
.
Теорема 1 - переформулировка общего критерия равномерного стремления функции к пределу.
Признаки равномерной сходимости интегралов
Теорема 2 (признак Вейерштрасса). Если существует неотрицательная для (х), определенная на промежутке [a;+) такая, что:
1. |f(x;y)|(х) xa, yY;
2.
 сходится,
сходится,
то интеграл (1) сходится равномерно относительно у на множестве Y.
Доказательство.
![]() 1) В силу признака сравнения интеграл
(1) абсолютно, а следовательно, и просто
сходится при любом yY
(из (1) и (2)).
1) В силу признака сравнения интеграл
(1) абсолютно, а следовательно, и просто
сходится при любом yY
(из (1) и (2)).
2) В силу сходимости
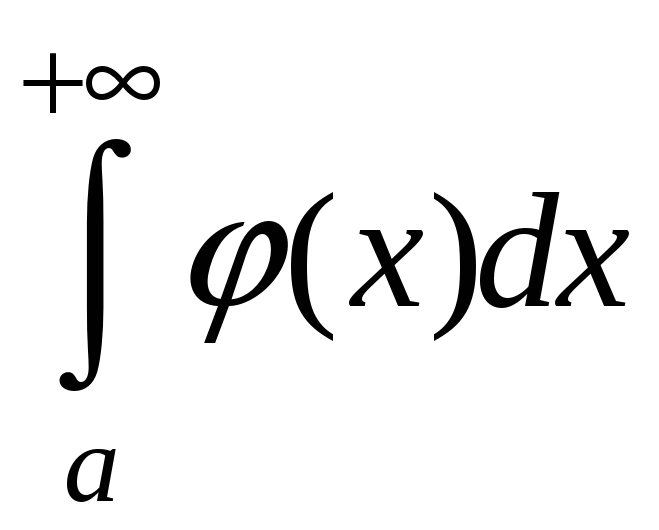 >0
A0a:
A>A>A0
выполнено
>0
A0a:
A>A>A0
выполнено
 .
.
3)
 .
.
По теореме 1 I(y)
равномерно сходится на Y.
![]()
Теорема
3. Пусть
функции f(x;y),
g(x;y)
определены при xa
и yY,
причем f(x;y)
непрерывна по переменной х,
а g(x;y)
имеет непрерывную по х
частную производную
![]() .
Если:
.
Если:
-
функция g(x;y) при каждом yY монотонна по х и равномерно на множестве Y стремится к нулю при
 ,
, -
интеграл
 ограничен как функция переменных
A[a;+)
и yY
на множестве
ограничен как функция переменных
A[a;+)
и yY
на множестве
 ;
;
то интеграл  (3)
(3)
равномерно сходится на множестве Y.
При доказательстве используем следующее утверждение.
Вторая теорема о среднем для интегралов.
Если: 1) функции f(x) и g(x) ограничены и интегрируемы на [a;b];
2) функция g(x) монотонна при x[a;b],
то  ,
где
,
где
![]() .
.
Доказательство теоремы 3.
![]() 1) Согласно
второй теореме о среднем для интегралов
при любых A,A:
a<A<A,
справедливо равенство:
1) Согласно
второй теореме о среднем для интегралов
при любых A,A:
a<A<A,
справедливо равенство:
 , (4)
, (4)
где
![]() .
.
(Предел не пишем, т.к. функция g(x;y) в силу дифференцируемости по х непрерывна по х).
2) По условию (п. 2)
 .
Тогда
.
Тогда
 . (5).
. (5).
Аналогично, 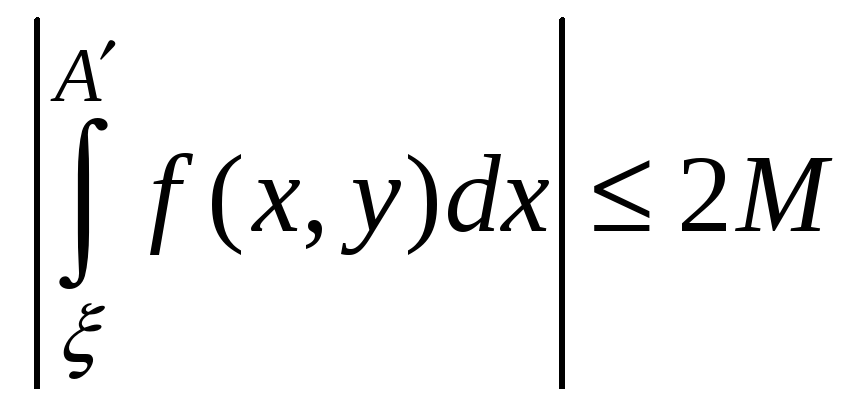 . (6)
. (6)
3) По условию
![]() .
По определению
.
По определению
![]()
![]() (8)
(8)
4) Из (4)-(7) следует
![]() имеет место оценка
имеет место оценка
 По
теореме 1 (критерий равномерной сходимости)
интеграл (3) равномерно сходится на
множестве Y.
По
теореме 1 (критерий равномерной сходимости)
интеграл (3) равномерно сходится на
множестве Y.
![]()
Теорема 4.
Если: 1) интеграл
 сходится равномерно на Y;
сходится равномерно на Y;
2) функция g(x;y) ограничена и монотонна по х,
то интеграл (3) сходится равномерно на множестве Y.
(Без доказательства.)
