
- •Тема 3. Методи розв’язування
- •1) Метод Гаусса-Жордана
- •Порядок заповнення розрахункової таблиці:
- •Алгоритм -го кроку методу Гаусса-Жордана
- •2) Похибки розв’язування систем лінійних алгебраїчних рівнянь методом Гаусса-Жордана
- •2) Інші прямі методи
- •2. Ітераційні методи розв’язування систем лінійних алгебраїчних рівнянь
- •Метод простої ітерації
- •4. Умови збіжності методу простої ітерації
- •Метод Зейделя
- •Тема 4. Методи розв’язування нелінійних рівнянь
- •1. Постановка задачі розв’язування нелінійного рівняння з одним невідомим. Відокремлення коренів.
- •Відокремлення коренів.
- •Способи відокремлення коренів
- •2. Метод поділу відрізку пополам (метод бісекції)
- •Алгоритм знаходження кореня рівняння методом поділу відрізку пополам
- •3. Метод хорд
- •Алгоритм знаходження кореня рівняння методом хорд
- •4. Метод дотичних (метод Ньютона)
- •Алгоритм знаходження кореня рівняння методом дотичних
- •5. Метод простих ітерацій
- •Алгоритм знаходження кореня рівняння методом простих ітерацій
4. Метод дотичних (метод Ньютона)
Нехай
функція
![]() двічі неперервно диференційована на
відрізку
двічі неперервно диференційована на
відрізку
![]() ,
причому похідні
,
причому похідні
![]() і
і
![]() не дорівнюють нулеві і зберігають знак
на цьому проміжку, а
не дорівнюють нулеві і зберігають знак
на цьому проміжку, а
![]() .
.
За
методом дотичних (методом Ньютона)
наближене значення кореня
![]() рівняння
(1)
знаходять як абсцису точки перетину
дотичної до кривої
рівняння
(1)
знаходять як абсцису точки перетину
дотичної до кривої
![]() в одній з точок
в одній з точок
![]() або
або
![]() з
віссю
з
віссю
![]() (мал.
27).
При
цьому змінна
(мал.
27).
При
цьому змінна
![]() наближається
до кореня лише з одного боку.
наближається
до кореня лише з одного боку.

Рівняння
дотичної,
яка проведена до кривої
![]() в
точці
в
точці
![]() ,
має вигляд:
,
має вигляд:
![]()
Наступне
наближення кореня
![]() знайдемо
як точку перетину дотичної з віссю
знайдемо
як точку перетину дотичної з віссю
![]() :
:
 .
.
Продовжуючи процес наближення, запишемо загальну формулу:
 ,
,
![]() (5)
(5)
Алгоритм знаходження кореня рівняння методом дотичних
-
Задати початкове наближення
 так, щоб виконувалася умова
так, щоб виконувалася умова
 .
Задати
точність
.
Задати
точність
 .
Покласти
.
Покласти
 .
. -
Обчислити
 за формулою (5).
за формулою (5). -
Якщо
 ,
процес закінчити і покласти
,
процес закінчити і покласти
 .
.
Якщо
![]() ,
покласти
,
покласти
![]() і перейти до п.2.
і перейти до п.2.
Приклад
6.
Знайти корінь рівняння
![]() (див. приклад 1) методом
дотичних з точністю
(див. приклад 1) методом
дотичних з точністю
![]() .
.
Розв’язання.
В прикладі 1 корінь рівняння було
відокремлено:
![]() .
Очевидно, функція неперервна на відрізку
.
Очевидно, функція неперервна на відрізку
![]() разом із своїми похідними
разом із своїми похідними
![]() ,
,
![]() .
Оскільки
.
Оскільки
![]() ,
,
![]() ,
а
,
а
![]() на відрізку
на відрізку
![]() ,
то
,
то
![]() .
Отже,
.
Отже,
![]() .
Результати розрахунків з використанням
формули (5) зведемо в таблицю:
.
Результати розрахунків з використанням
формули (5) зведемо в таблицю:
-



0
–2
–
1
–1,545455
0,454545
2
–1,359615
0,185840
3
–1,325801
0,033814
4
–1,324719
0,001082
5
–1,324718
0,000001
Оскільки
![]() ,
то процес завершується: корінь
рівняння
,
то процес завершується: корінь
рівняння
![]() .
.
5. Метод простих ітерацій
Нехай
знайдений такий відрізок
![]() ,
що
,
що
![]() ,
і на кінцях відрізку функція
,
і на кінцях відрізку функція
![]() ,
яка визначає рівняння
,
яка визначає рівняння
![]() ,
набуває значення різних знаків, тобто
,
набуває значення різних знаків, тобто
![]() .
.
Алгоритм знаходження кореня рівняння методом простих ітерацій
-
Рівняння
 перетворити до рівносильного вигляду
перетворити до рівносильного вигляду
 .
Для збіжності процесу ітерацій необхідно,
щоб виконувалась умова збіжності
.
Для збіжності процесу ітерацій необхідно,
щоб виконувалась умова збіжності
 ,
де
,
де
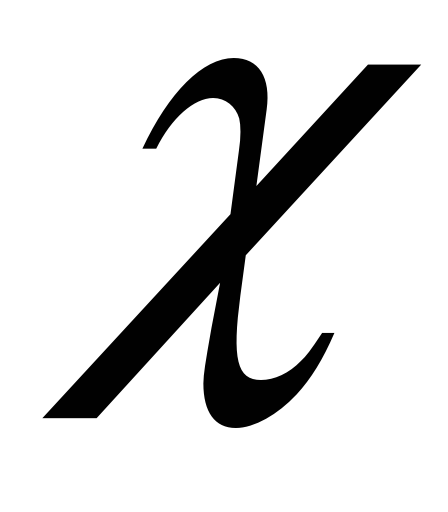 – деяка константа. При цьому задача
зводиться до знаходження абсциси точки
перетину прямої
– деяка константа. При цьому задача
зводиться до знаходження абсциси точки
перетину прямої
 і кривої
і кривої
 .
. -
Задати початкове наближення
 .
Задати
точність
.
Задати
точність
 .
Покласти
.
Покласти
 .
. -
Обчислити
 за формулою
за формулою
![]() (6)
(6)
-
Якщо
 ,
процес закінчити і покласти
,
процес закінчити і покласти
 .
.
Якщо
![]() ,
покласти
,
покласти
![]() і перейти до п.3.
і перейти до п.3.
Приклад
7.
Знайти корінь рівняння
![]() (див. приклад 1) методом
простих ітерацій з точністю
(див. приклад 1) методом
простих ітерацій з точністю
![]() .
.
Розв’язання.
В прикладі 1 корінь рівняння було
відокремлено:
![]() .
Перетворимо рівняння до вигляду
.
Перетворимо рівняння до вигляду
![]() .
Для цього запишемо його у формі
.
Для цього запишемо його у формі
![]() .
Але функція
.
Але функція
![]() не задовольняє умові збіжності на
відрізку
не задовольняє умові збіжності на
відрізку
![]() ,
оскільки
,
оскільки
![]() ,
,
![]() ,
,
![]() .
.
Скористаємося
іншим перетворенням. Отримаємо
![]() .
Функція
.
Функція
![]() задовольняє умові збіжності на відрізку
задовольняє умові збіжності на відрізку
![]() ,
оскільки
,
оскільки
 ,
,
![]() ,
,
![]() .
.
Задамо
початкове наближення
![]() .
.
Результати розрахунків з використанням формули (6):
![]()
зведемо в таблицю:
-



0
–1
-
1
–1,2599
0,2599
2
–1,3123
0,0524
3
–1,3223
0,0100
4
–1,3243
0,0020
5
–1,3246
0,0003
Оскільки
![]() ,
то процес завершується: корінь
рівняння
,
то процес завершується: корінь
рівняння
![]() .
.
