Тема 5. Описательная статистика.

5.1 Измерение центральной тенденции и вариации признака.

В социальных исследованиях важное место занимает измерение центральной тенденции, состоящее в выборе такого показателя, который наилучшим образом описывает все значения признака из набора данных.

Наиболее распространенной формой показателей, используемой в социальных исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты изучаемого явления и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Широкое применение средних объясняется тем, что они имеют ряд положительных свойств, делающих их незаменимыми в анализе явлений и процессов общественной жизни. Важнейшим из этих свойств является то, что средняя величина отражает общее, присущее всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности варьируют под влиянием множества факторов, среди которых могут быть как основные, так и случайные. В средней взаимно погашаются те отклонения значений признака, которые обусловлены действием случайных факторов, и учитываются изменения, вызванные действием факторов основных, что позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.

Для каждого показателя, используемого в социальном анализе, можно составить только одно истинное исходное соотношение средней. Однако от того, в каком виде представлены исходные данные, зависит, каким именно образом исходное соотношение средней будет реализовано. Средние показатели могут рассчитываться по дискретным и интервальным вариационным рядам. Рассмотрим расчет средней на конкретных примерах.

Среднее, определяемое как отношение суммы всех значений выборки к ее объему:

Задача: представлены данные для выборки из семи значений 2,2,4,5,10,6,1

Пример расчета:

Среднее для сгруппированных данных, определяемое как сумма произведений значений признака на частоту, отнесенная к объему выборки

Задача: представлены данные об оценках, полученных студентами на экзамене:

Оценка	Число студентов
xi	fi	xi fi
5	17	85
4	41	164
3	20	60
2	7	14
итого	85	323

Пример расчета:

Среднее для интервального распределения, определяемое как сумма произведений частот на величину середины интервала, отнесенная к объему выборки:

Задача: представлены данные о доходах населения города N:

Доход, руб.	Численность населения, %	Середина интервала
xi	fi	mi	fimi
до 4000	25	3000	75000
4000-6000	15	5000	75000
6000-8000	35	7000	245000
8000-10000	10	9000	90000
свыше10000	15	11000	165000
	100		650000

Пример расчета:

Взвешенное среднее значение, получаемое при объединении нескольких групп наблюдений:

Группа	Среднее по группе, Вес, кг	Объем группы, чел.
	x	n
A	87	65
B	92	110
C	89	85
D	96	200
E	84	60
Итого		520

Пример расчета:

Среднее для дихотомической шкалы определяется как частное от числа единиц к числу элементов выборки:

Задача: представлены данные для выборки из десяти значений 1,0,0,0,1,1, 1,1,1,0

Пример расчета:

Вывод: 60% значений выборки принимают значение, равное единице, а 40% – значение ноль.

Описание центральной тенденции возможно при помощи таких понятий, как мода и медиана.

Мода (Мо) – значение признака, наиболее часто встречающегося в исследуемой совокупности.

Медиана (Ме) – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.

Для дискретных вариационных рядов модой является значение варианта с наибольшей частотой, медианой – вариант, находящийся в середине ранжированного ряда (в случае, когда ряд имеет нечетное число членов) и медиана – среднее арифметическое из двух значений признака, расположенных в середине ряда (в случае, когда ряд имеет четное число членов). Рассмотрим конкретные примеры вычисления этих величин.

Условия задачи

Решение

Представлено распределение данных о выборе дисциплин студентами вуза:

Дисциплины	f
Антропология	97
Экономика	104
Политика	110
Психология	72
Информатика	109
Социология	149
того	641

Значение моды соответствует максимальной частоте:

f_max = 149,

поэтому

Мо=149

Представлен вес тела для двух групп людей:

Вес (фунты)	Группа 1 f1	Группа 2 f2
190-199	3	3
180-189	2	8
170-179	4	21
160-169	10	7
150-159	13	9
140-149	23	6
130-139	12	7
120-129	7	20
110-119	3	3
100-109	3	2
Всего	80	86

Величина интервала для двух групп одинакова и равна 9 фунтам, середина интервала составляет 4,5 фунтов, значение моды приходится на середину того интервала, частота которого максимальна.

Для первой группы:

f_{1 max} = 23,

Мо =140+4,5=144,5

Для второй группы:

f_{2 max} = 21 и близкое

ему значение f_{2 max} = 20

(такое распределение

называют бимодальным),

Мо =170+4,5=174,5

Мо =120+4,5=124,5

Представлена выборка четного и нечетного размера одежды:

Выборка 1 (n=5)	Выборка 2 (n=6)
198	197
179	193
172	189
167	187
154	183
	179

Для нечетного числа наблюдений (n=5)

медианой является наблюдение

с номером (n+1)/2

Для первой группы:

(5+1)/2 = 3, т.е. Me = 172.

Для четного числа наблюдений (n=6)

медианой является среднее значение наблюдений с номерами n/2 и (n+2)/2

Для второй группы:

6/2=3 и (6+2)/2=4, т.е.

Как в случае четного, так и в случае нечетного числа наблюдений, медиана является серединой выборки.

Исследование вариации в социальных исследованиях имеет важное значение, так как величина вариации признака в статистической совокупности характеризует ее однородность.

В статистической практике для изучения и измерения вариации используются различные показатели (меры) вариации в зависимости от поставленных перед исследователем задач. К ним относятся размах вариации, среднее линейное отклонение, средний квадрат отклонений (дисперсия), среднее квадратическое отклонение и коэффициент вариации.

При изучении вопроса о вариации нужно четко представлять себе условия, порождающие вариацию признаков, а также сущность и значение измерения вариации признаков. Следует также усвоить, что изучение вариации признаков общественных явлений находится в прямой связи с группировками, в частности с рядами распределения. Очень важно научиться свободно исчислять все показатели вариации.

Размах вариации (R) является наиболее простым измерителем вариации признака.

R = х_max – х_min,

где х_min – наименьшее значение варьирующего признака;

х_max — наибольшее значение признака.

Среднее значение признака

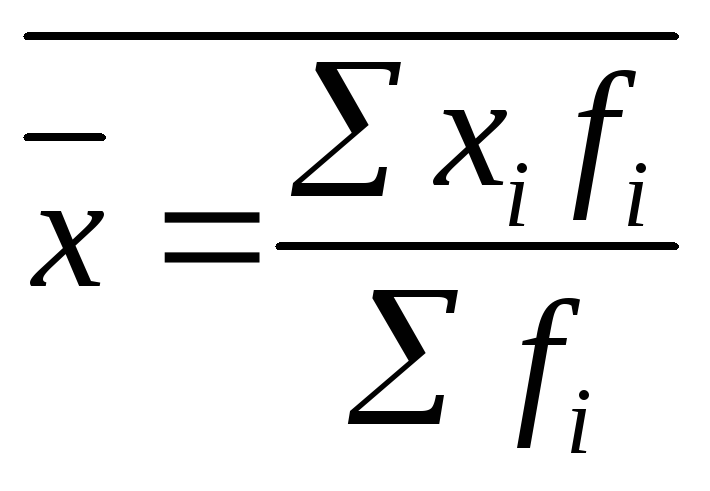как взвешенное значение

xi	fi
2	4
5	3
88	6
34	8

Среднее линейное отклонение (d) представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения:

– невзвешенное среднее линейное отклонение;

– взвешенное среднее линейное отклонение.

Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

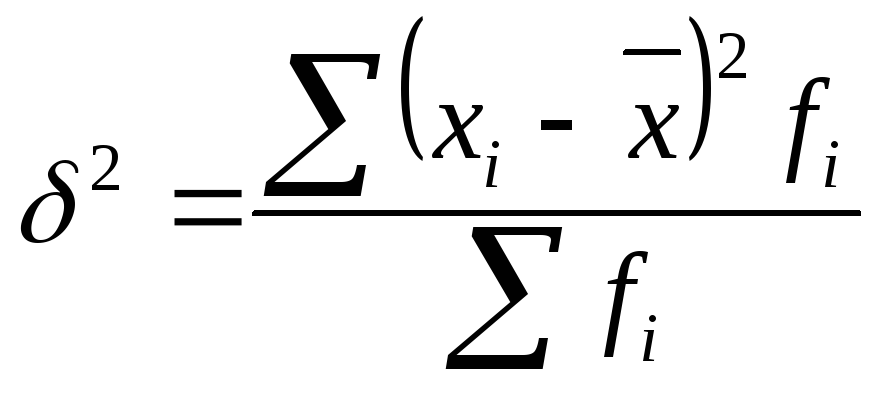– взвешенная дисперсия

Среднее квадратическое отклонение – корень второй степени из среднего квадрата отклонений индивидуальных значений признака от их средней величины.

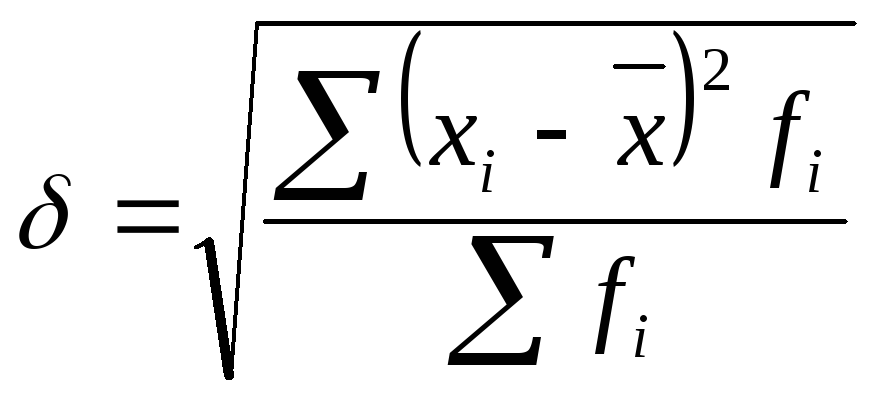
Дисперсия и среднее квадратическое отклонение являются наиболее широко применяемыми показателями вариации, что объясняется тем, что они входят в большинство теорем теории вероятностей, служащей фундаментом математической статистики. Кроме того, дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов, обуславливающих вариацию признаков. Дисперсия используется для построения показателей тесноты корреляционной связи, при оценке результатов выборочных наблюдений и т.д.

Среднее квадратическое отклонение и среднее линейное отклонение показывают, насколько в среднем колеблется величина признака у единиц исследуемой совокупности. По свойству мажорантности средних величин среднее квадратическое отклонение всегда больше среднего линейного отклонения. Если распределения признака близко к нормальному (т.е. значения моды, медианы и среднего практически совпадают), то между этими величинами существует взаимосвязь:

δ≈1,25d или d ≈ 0, 8δ

Среднее квадратическое отклонение показывает, как расположена основная масса единиц относительно средней арифметической. В соответствии с теоремой П.Л. Чебышева (1821 – 1894) можно утверждать, что независимо от формы распределения 75% значений признака попадают в интервал ± 2 δ, а по крайней мере 89% всех значений признака попадают в интервал ± 3 δ.

Пример: на основе данных о распределении учителей района по стажу работы рассчитать показатели вариации.

Стаж работы, лет xi	Число учителей, % к итогу fi	xi fi	xi -	│ xi - │fi	│ xi - │^2	│ xi - │^2fi
8	14	112	-2	28	4	56
9	20	180	-1	20	1	20
10	30	300	0	0	0	0
11	24	264	1	24	1	24
12	12	144	2	24	4	48
Итого	100	1000		96		148

Пример расчета:

Размах вариации стажа	R =12—8 =4 года.
Средний стаж работы	лет
Среднее линейное отклонение	года
Дисперсия

Основная формула для расчета дисперсии:

– невзвешенная дисперсия

Пример расчета дисперсии для уровня бедности, тыс.руб./чел./мес.

	Центр города				Окраина города
		x			x
1		24,5			27,4
2		23,8			24,6
3		23,1			23,0
4		22,4			22,5
5		21,7			21,8
6		21,0			21,6
7		21,0			20,9
8		20,3			19,7
9		19,6			18,1
10		19,6			17,4
		∑ =217,0		∑ = 26,46	∑ = 217,0		∑ = 79,34

Для центра = 26,46, для окраины = 79,34

Таким образом, вариация доходов в центре ниже, чем на окраине.

Другая формула для расчета дисперсии выборки:

Пример расчета дисперсии: имеется выборка из четырех значений

2,3,6,9

2
3
6
9
∑ = 20	∑ = 130

= 10

Дисперсия для сгруппированных данных:

Пример расчета дисперсии

Стаж работы	F	x (середина интервала)	fx	fx^2
2-4	2
5-7	5
8-10	10
11-13	4
14-16	2
	∑ = 23		∑ = 204	∑ =2034

= 10,2

Стандартное отклонение – квадратный корень из дисперсии

Стандартное отклонение интерпретируется как мера разброса, так как имеет те же единицы измерения, как и результаты наблюдений.

Дисперсия измеряется как первоначальные единицы измерения в квадрате.

Для целей сравнения вариации различных признаков в одной и той же совокупности или же при сравнении вариации одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха, или среднего линейного отклонения, или среднего квадратического отклонения к средней арифметической. Чаще всего они выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Различают следующие относительные показатели вариации

Коэффициент осцилляции: 100%

Линейный коэффициент вариации: 100%

Коэффициент вариации: 100%

Наиболее часто используется коэффициент вариации, например, в случаях, когда необходимо сравнить несколько совокупностей, измеряемых в разных величинах или сравнить несколько совокупностей, измеряемых в одинаковых величинах, но имеющие сильно отличающиеся средние.

Пример: по имеющимся данным для двух совокупностей, выявить, различие в вариации признака: δ₁ = 3, , δ₁ = 20, .

Пример расчета:

и

Вывод – коэффициенты вариации равны, поэтому вариация признака в сравниваемых совокупностях одинакова.

Пример: в городе N в 2008 г. средняя цена 1 м² жилья составила 30,88 тыс. руб., а в 2009 г. – 50,82 тыс. руб. Известно, что среднее квадратическое отклонение в 2008 г. составило 7,6, а в 2009 г. – 9,8. Необходимо сделать выводы о вариации цен за жилье.

Пример расчета:

или 25%, или 19%.

Вывод – так как значение второго коэффициента меньше, чем первого, то вариация цен за жилье в 2009 г. снизилась по сравнению с 2008 г.

В социологических исследованиях часто возникает необходимость оценки вариации качественных признаков, эквивалентом которых будет служить бинарная переменная со значениями 0 и 1. Например, при изучении успеваемости студентов, их можно разделить на две группы – успевающих и неуспевающих, причем значение 1 присваивается успевающему студенту.

Пример: имеются данные для совокупности, число единиц которой равно n, а число единиц, обладающих признаком – f.

Значение переменной	Частота	Число студентов
1	f	40
0	n-f	20
Итого	n	60

Пример расчета средней арифметической предложенного ряда:

= p,

Таким образом, значение средней арифметической равняется относительной частоте, т.е. p – доля единиц, обладающих этим признаком, а доля единиц, не обладающих этим признаком – q (как известно, p + q = 1).

Тогда дисперсия альтернативного (бинарного) признака:

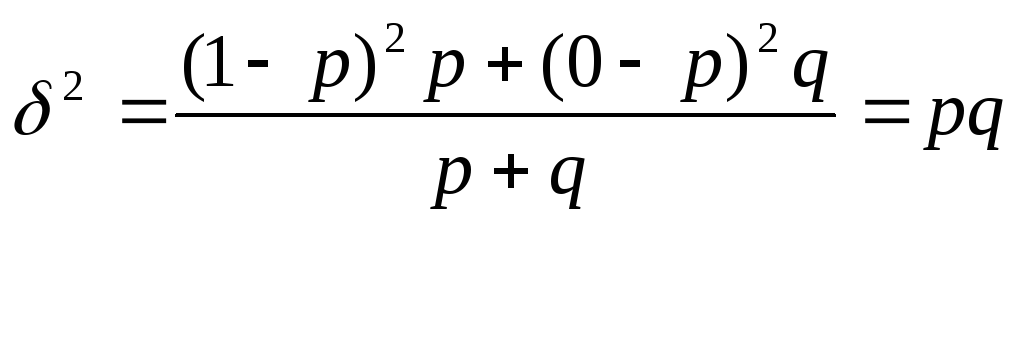
Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и оценку его симметричности островершинности или плосковершинности. Симметричным называется распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. В статистике дня характеристики асимметрии пользуются несколькими показателями.

Квартиль (Q) – значение признака, делящее ранжированную совокупность на четыре равновеликие части.

Нижний квартиль Q₁ отделяет ¼ часть совокупности с наименьшими значениями признака (то есть 25% единиц будут иметь значения признака, меньшими по величине, чем Q₁), а верхний Q₃ отделяет ¼ часть совокупности с наибольшими значениями признака. Средний квартиль Q₂ является медианой. Между Q₁ и Q₃ располагается 50% всех данных. Квартильный размах находится по формуле:

IQR = Q₃ – Q₁

Зачастую при анализе данных встречаются такие значения признака, которые значительно отличаются от основного массива данных – они носят название выбросов. Исследователь сам принимает решение о дальнейшей работе с ними; если выбросы оставляются, то проводят два исследования – с ними и без них, а результаты сопоставляются, если выбросы исключаются, то это действие должно быть аргументировано в отчете. Количественная оценка выбросов дается с помощью понятия квартиля.

Умеренные выбросы располагаются ниже первой квартили или выше третьей на расстояниях от 1,5 до 3 IQR. Экстремальные выбросы располагаются ниже первой квартили или выше третьей на расстояниях свыше 3 IQR .

При проведении анализа важное значение имеет графическое изображение медианы, максимального и минимального значений, что возможно продемонстрировать с помощью коробковой диаграммы, реализуемой в программе SPSS. По виду и размеру коробки можно также судить о том, где расположены 50% данных.

Пример: имеются данные о возрасте некоторого числа мужчин и женщин, работающих в сфере образования. Отчет в программе SPSS выглядит следующим образом:

Характеристика	Мужчины	Женщины
Минимум	31	21
Первая квартиль	37	30
Медиана	43	34
Третья квартиль	51	41
Максимум	76	80
Квартильный размах	14	11
Среднее	44	34

Данные таблицы позволяют отметить, что средний возраст мужчин выше, чем у женщин. 50% данных, как было указано выше, располагаются между первой и третьей квартилью, что для женщин составляет возраст между 30 и 41 годами, для мужчин – между 37 и 51 годами.