105. Эллипс Эллипс – геометрическое место точек на пл-ти, сумма расстояний от каждой икоторых до 2 заданных точек f1 и f2, называемых фокусами постоянна и равна 2a.
x2/a2 + y2/b2=1 = 1 –каноническое уравнение эллипса. 0>E<1.
Факальный параметр p=b2/a, r=p/(1+Ecosφ) – полярное ур-ие.
r1+r2=2a – большая ось.
2b – малая ось.
2с – расстояние между фокусами. b2 =a2-c2.
Е=с/а – эксцентриситет.
Эксцентриситетом наз. отношение его фокального расстояния большей полуоси. Для эллипса e=c/a. Он может быть = 0 (окружность). При Эксцентриситете = 1, эллипс вырождается в отрезок. Половине может быть равен. Двум не может быть равен, т.к расстояние между фокусами меньше главной оси.
Е=0 c=0 – окружность радиуса а. Е=1 c=a – отрезок.
a11x2 +2a12xy + a22y2 + 2a20y+ a00=0, где а11,а12,а22,а10,а20,а00 – действительные числа, причём а111, а12, а22 одновременно не равны 0.
106. Гипербола
Гипербола – геометрическое место точек модуль разности расстояний от которых до двух заданных точек(фокусов) постоянен. ׀v1-v2׀=2a/
x2/a2 - y2/b2=1 – каноническое ур-ие гиперболы.
b2=c2-a2.
E=c/a E>1.
y=(±b/a)x. r=p/(1+Ecosφ) – полярное ур-ие.
Прямые L1 и L2, уравнения которых у=+- (b/a)х называются асимптотами гиперболы, где а и b действительные мнимые полуоси гиперболы.
108. Кривые второго порядка.
Множество точек плоскости M(х,у) , координаты х и у которых удовлетворяет уравнению
a11x2 +2a12xy + a22y2 + 2a20y+ a00=0, где а11,а12,а22,а10,а20,а00 – действительные числа, причём а111, а12, а22 одновременно не равны 0, называется кривой второго порядка. Причем ур наз. общим уравнением кривой.
111. Парабола
Парабола - геометрическое место точек пл-ти, равнгоудаленных от данной точки(фокуса)и данной прямой (директриса). у2=2рх.
Параболой наз. множество всех точек плоскости, расстояние от каждой из которых до каждой точки f равно расстоянию до данной прямой d не проходящей через точку f. Прямая d явл. Её директрисой, ур-е которой х+ р/2 =0
112. Эллипс Эллипс – геометрическое место точек на пл-ти, сумма расстояний от каждой икоторых до 2 заданных точек f1 и f2, называемых фокусами постоянна и равна 2a.
x2/a2 + y2/b2=1 = 1 –каноническое уравнение эллипса. 0>E<1.
Факальный параметр p=b2/a, r=p/(1+Ecosφ) – полярное ур-ие.
r1+r2=2a – большая ось.
2b – малая ось.
2с – расстояние между фокусами. b2 =a2-c2.
Е=с/а – эксцентриситет.
Эксцентриситетом наз. отношение его фокального расстояния большей полуоси. Для эллипса e=c/a. Он может быть = 0 (окружность). При Эксцентриситете = 1, эллипс вырождается в отрезок. Половине может быть равен. Двум не может быть равен, т.к расстояние между фокусами меньше главной оси.
Е=0 c=0 – окружность радиуса а. Е=1 c=a – отрезок.
113. Гипербола
Гипербола – геометрическое место точек модуль разности расстояний от которых до двух заданных точек(фокусов) постоянен. ׀v1-v2׀=2a/
x2/a2 - y2/b2=1 – каноническое ур-ие гиперболы.
b2=c2-a2.
E=c/a E>1.
y=(±b/a)x. r=p/(1+Ecosφ) – полярное ур-ие.
Прямые L1 и L2, уравнения которых у=+- (b/a)х называются асимптотами гиперболы, где а и b действительные мнимые полуоси гиперболы.
114. Выпуклое множество
Мн-во MАn называется выпуклым, если для любых 2-х точек А и В этого мн-ва отрезок АВ также лежит в мн-ве М (напр. куб, шар, квадрат, круг, пирамида, эллипс).
Пересечение нескольких выпуклых множеств есть выпуклое множество.
115. Выпуклая область
Пересечение нескольких полупространств в Аn называется выпуклой многогранной областью в Аn.
В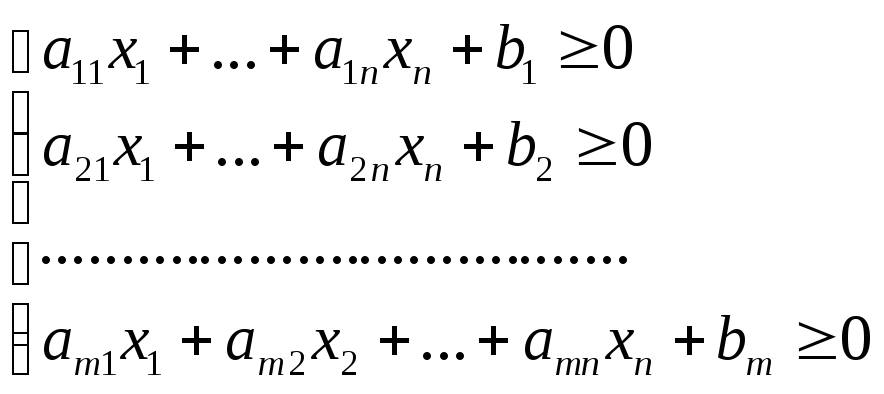
ыпуклая
многогранная область
В свою очередь, полупространством в An – называется множество точек x(x1,x2,…,xn) таких, что
a1x1+a2x2+…+anxn+b0
a12+a22+…+an2>0
a1, a2,…,an, b – фиксированные числа.
116. Выпуклая область. Пересечение нескольких выпуклых множеств есть выпуклое множество.
Пересечение нескольких полупространств в Аn называется выпуклой многогранной областью в Аn.
В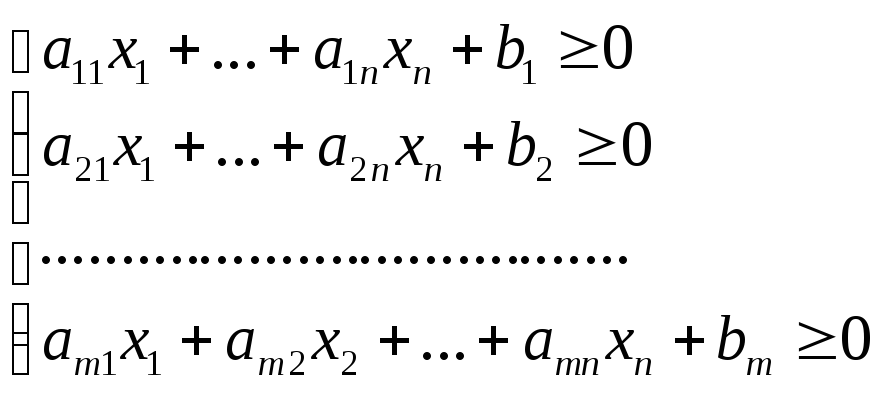
ыпуклая
многогранная область
В свою очередь, полупространством в An – называется множество точек x(x1,x2,…,xn) таких, что
a1x1+a2x2+…+anxn+b0
a12+a22+…+an2>0
a1, a2,…,an, b – фиксированные числа.
Пересечение нескольких выпуклых множеств есть выпуклое множество.
Согласно теореме о вып. множествах. Согласно лемме пересечение нескольких выпуклых множество есть выпуклое множество. Действительно пусть М=М1∩М2, где М1 и М2 выпуклы. Пусть А€ М И В€ М. тогда А €М1 И В€ М1. т. к. М выпуклое, то это означает, что отрезок АВ содержится в М1что означает выпуклость М, чтд.