§3.5. Решение уравнения Шредингера одномерного осциллятора при помощи операторов рождения и уничтожения

Существует более простой и современный метод решения уравнения Шредингера гармонического осциллятора, основанный на представлениях об операторах рождения и уничтожения. Кроме того, в этом параграфе воспользуемся формализмом Дирака.

Введем операторы:

, . (3.68)

Прямым вычислением легко показать, что их коммутатор

[]=1. (3.69)

Гамильтониан одномерного квантового осциллятора записывается с помощью этих операторов в виде

. (3.70)

Удобно определять в дальнейшем энергию в единицах тогда . Используя (3.69), нетрудно показать, что

. (3.71)

Пусть - нормированное собственное состояние с энергией

E_n = n+1/2, т.е.

. (3.72)

^Тогда и - собственные состояния (ненормированные) с энергией +1 и 1 ^{соответственно. Действительно,}

, (3.73)

. (3.74)

Таким образом, действие оператора на состояние переводит его в состояние , то есть повышает энергию состояния на единицу,, а действие оператора a на состояние переводит его в состояние , то есть понижает энергию состояния на единицу.

Интерпретация: состояние содержит n одинаковых частиц (квантов) с энергией E = каждая. Оператор называют повышающим оператором или оператором рождения такой частицы, а оператор - понижающим оператором или оператором уничтожения. Состояние , соответствующее условию n=0 (отсутствию возбуждений) называется основным состоянием. Понизить энергию этого состояния нельзя, поэтому это состояние должно удовлетворять уравнению .

Заметим, что собственные значения оператора

(3.75)

равны n, поэтому называют оператором числа частиц. Найдем коэффициент c_n . Для этого вычислим норму вектора :

_{= .} (3.76)

Таким образом, нормированное состояние должно быть определено, как

. (3.77)

Отличные от нуля матричные элементы операторов рождения и

_{уничтожения равны}

^. (3.78)

Прямым вычислением легко показать, что

, ,

.

Как уже отмечалось, волновая функция основного состояния может быть найдена из условия

. (3.79)

Это сразу же дает

. (3.80)

Для волновой функции с n >0 получаем компактное выражение

. (3.81)

Очевидно, что эти состояния (волновые функции) ортонормированны. Это легко показать, используя соотношения коммутации (3.69) и условие (3.79).

Квантовый осциллятор в электрическом поле. Гамильтониан одномерного осциллятора в электрическом поле F , направленном вдоль оси х, имеет вид

(3.82)

где .

Введём операторы , тогда

. (3.83)

Все коммутационные соотношения для новых операторов совпадают с коммутационными соотношениями для операторов и . Очевидно, что

, (3.84)

где

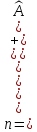. (3.85)

Рассмотрим оператор координаты

. (3.86)

В отсутствии поля все малые колебания происходят вокруг . Электрическое поле просто сдвигает положение из нуля в точку .