
- •Vector spaces
- •1.2. Линейные (векторные) пространства.
- •1.3. Линейная зависимость, независимость, базисы.
- •1.4. Морфизмы и матрицы.
- •1.5. Дуальное пространство.
- •1.6. Связь с линейными уравнениями.
- •1.7. Инвариантные подпространства.
- •1.8. Многочлены от операторов и матриц.
- •1.9. Полилинейные формы.
ГОУ Школа-интернат «Интеллектуал» Абрамсон Я.И.
Vector spaces
Начнём с более общего понятия, к которому мы будем время от времени возвращаться, но систематически изучать его не предполагаем: надо же оставить что-то и для высшей школы!
1.1. Модули.
Рассмотрим действие R на G, в котором G не просто «множество», а группа, причём абелева (записываемая аддитивно), а R – не просто группа, а кольцо, причём коммутативное и с единицей.
Т
 .е.,
помимо того, что R действует
на G как (мультипликативный)
моноид (1g=g
gG
и (st)g=s(tg)
s,t
R,
gG),
операции сложения в кольце и группе
коммутируют с операцией действия:
(r1+r2)
g= r1×g+r2×g
и r×(g1+g2)=r×g1+r×g2.
Первое из этих равенств означает, что
каждый элемент абелевой группы G
выступает в качестве гомоморфизма
абелевой группы R в абелеву
группу G:gHom(R,G).
Второе означает, что каждый элемент
кольца R можно рассматривать,
как эндоморфизм группы G:
rEndG.
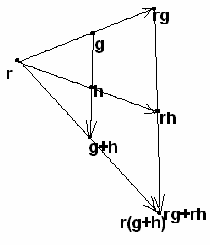
Иллюстрируют эту ситуацию две
схемы:
.е.,
помимо того, что R действует
на G как (мультипликативный)
моноид (1g=g
gG
и (st)g=s(tg)
s,t
R,
gG),
операции сложения в кольце и группе
коммутируют с операцией действия:
(r1+r2)
g= r1×g+r2×g
и r×(g1+g2)=r×g1+r×g2.
Первое из этих равенств означает, что
каждый элемент абелевой группы G
выступает в качестве гомоморфизма
абелевой группы R в абелеву
группу G:gHom(R,G).
Второе означает, что каждый элемент
кольца R можно рассматривать,
как эндоморфизм группы G:
rEndG.
Иллюстрируют эту ситуацию две
схемы:
Упражнение 1.
Являются ли возникающие отображения GHom(R,G) и REndG гомоморфизмами групп?.
И вот, если мы имеем дело с описанной выше ситуацией (т.е., когда коммутативное кольцо с единицей R действует на абелеву группу G), то говорят, что G – левый R-модуль или левый модуль над кольцом R. Левым его называют только потому, что мы операцию действия записываем так: слева элемент из R, справа – из G. Если бы записывали в обратном порядке, то G бы называлась правым R-модулем.
Естественно подмодулем G назвать такую подгруппу G, которая сама была бы R-модулем. Для этого необходимо и достаточно, чтобы действие R на элементы этой подгруппы не выводило бы их за её пределы. Итак, подгруппа НG называется ( левым R-) подмодулем (левого R-) модуля G, если RНН.
Упражнение 2 (Примеры).
Рассмотрим множество всех многочленов с целыми коэффициентами. Проверьте, что это – модуль над кольцом Z. Найдите в нём его подмодули.
Любое кольцо является модулем над самим собой.
Любая абелева группа является Z-модулем.
Левый идеал кольца R является модулем над ним.
Пусть -левый идеал кольца R, М – левый R-модуль. Тогда множество всевозможных конечных сумм М=a1х1+a2х2+…+anxn, где aia и xiM является подмодулем М.
Упражнение 3.
Пусть М - R-модуль, а R и R – (левые) идеалы кольца R. Тогда:
(М)=()М и (+)М=М+М.
Упражнение 4.
Если N1 и N2 – подмодули М, то (N1+N2)=N1+N2.
Упражнение 5.
Пересечение R-модулей - R-модуль. Объединение возрастающей цепочки R-модулей - R-модуль.
Упражнение 6.
Пусть N – подмодуль модуля М над R. Дайте определение фактор-модуля М/N. Проверьте его корректность и сам факт того, что построенный фактор-модуль М/N будет действительно R-модулем.
Определение.
Как всегда, когда мы вводим новый объект ( в данном случае – модули), мы даём определение подобъекта (подмодуля), его фактора (фактор-модуля) и его морфизмов. Морфизмы модулей называются, как и в случае групп и колец, гомоморфизмами. Под гомоморфизмом R-модулей М и M` понимается их гомоморфизм как групп, который коммутирует с действием кольца: f:MM`; f(rm)=rf(m) rR, mM.
Говорят также, что f – R-линейное отображение.
Упражнение 7.
Пусть N – подмодуль модуля М над R. Проверьте, что канонический гомоморфизм (это гомоморфизм mm+N) аддитивных групп f:M М/N является также гомоморфизмом модулей.
Упражнение 8.0.
Пусть М – модуль над R. Докажите, что r0=0 (0 – нейтральный элемент М, произвольный элемент кольца R).
Упражнение 8.
Если f:MM` гомоморфизм модулей, то его ядро и образ являются подмодулями в М и M` соответственно.
Определение.
П оследовательность
гомоморфизмов модулей
оследовательность
гомоморфизмов модулей
![]() называется
точной,
если Imf=Kerg.
Графически это можно изобразить так:
называется
точной,
если Imf=Kerg.
Графически это можно изобразить так:
Упражнение 9.
Пусть N – подмодуль модуля М и NМ – вложение (хх),а M М/N – канонический гомоморфизм. Тогда последовательность 0NM М/N0 точна.
На этом мы временно попрощаемся с модулями. Их свойства сильно зависят от качества того самого кольца R, над которым они модули. Чем «лучше» R (область целостности, кольцо главных идеалов и т.п.), тем больше можно сказать о модулях над ним. Самое простое кольцо – это поле. Вот над ним-то мы теперь и будем рассматривать модули.
