К

ГОУ Школа-интернат «Интеллектуал» Абрамсон Я.И. 06.09.2010.

онспект №6. Введение в теорию групп.

1. Основные понятия и определения.

Def. Группой G называется множество М c заданной на нём ассоциативной операцией * с такими свойствами:

• существует, по крайней мере, один правый нейтральный элемент, т.е. такой элемент е, что для всех элементов m множества М mе=m и, по крайней мере, один левый нейтральный элемент, т.е. такой элемент f, что для всех элементов m множества М fm=m.

• Для каждого элемента m множества М существует, по крайней мере, один правый обратный к нему элемент m_п^-1 такой, что mm_п^-1=е и, по крайней мере, один левый обратный к нему элемент m_л^-1 такой, что m_л^-1m=е.

В аддитивной форме записи вместо знака  используют знак + и говорят о сложении, нулевом и противоположном элементах, в мультипликативной записи вместо знака  используют знак  и говорят об умножении, единичном и обратном элементах. Обратные элементы записываются как (-m_п) или (-m_л) Например, в аддитивной записи свойство ассоциативности выглядит так: (а+b)+с=а+(b+с) a,b,cM а в мультипликативной записи это же свойство записывается так: (аb)с=а(bс) a,b,cM.

Если операция ещё и коммутативна, то такая группа называется абелевой.

Упражнение №1.

Докажите, что на самом деле в группе G=(М,*) существует лишь один нейтральный элемент. То есть, все правые и левые «нули» (соответственно, «единицы») совпадают.

Упражнение №2.

Докажите, что на самом деле в группе G=(М,) у каждого элемента существует лишь один обратный элемент. То есть, все правые и все левые обратные (противоположные) элементы к одному и тому же элементу совпадают.

Def. Подмножество NM c той же операцией  называется подгруппой Н группы G, если оно само является группой относительно заданной операции. Это значит, что операция  не выводит за пределы N (говорят, что N замкнуто относительно операции ) и обратный к каждому элементу N также является элементом N (то есть, что и относительно отображения m→m^-1 N также замкнуто).

Примеры.

(В скобках указана операция, относительно которой рассматриваемое множество является группой). Множество целых чисел относительно сложения: (Z,+). Её подгруппы – кратные любого числа m: mZ.

Упражнение №3.

Докажите, что этими подгруппами исчерпываются все подгруппы группы Z.

Указание. Используйте алгоритм Евклида и метод доказательства «от противного».

Рациональные числа Q относительно сложения: (Q,+). Рациональные числа без нуля по умножению: (Q\{0},ⅹ). Её подгруппа: положительные рациональные числа: (Q⁺, ⅹ). Другие подгруппы: {Q_p,+} все рациональные ненулевые числа со знаменателями – степенями некоторого простого числа р. То есть числа вида .

Следующий пример: множество G всех функций, заданных на множестве М, {f: MQ} с операцией сложения. Пусть М=R. Тогда подгруппой группы G всех функций (предыдущий пример) будет, например, подмножество НМ функций, состоящее из всех многочленов. В свою очередь, подгруппой KH, будет, например, множество всех многочленов степени не выше четвёртой. Другую подгруппу группы G образуют все чётные функции. Равно как и нечётные функции. Проверьте, что это именно так во всех приведённых выше примерах, а также в следующих ниже.

Все биекции (автоморфизмы) данного множества М относительно операции композиции (последовательного выполнения). Эта группа обозначается как AutM.

В случае, когда множество M конечно, эти биекции называют подстановками (или перестановками). Иногда подстановкой называют двухрядную запись, а под перестановкой имеют ввиду нижний ряд этой записи, то есть сам результат операции. Пусть, например, некоторое множество М состоит из трёх элементов, которые мы и обозначим их номерами: 1,2,3. Рассмотри биекцию : М → М (перестановки обычно обозначают греческими буквами) при которой (1)=2; (2)=3 и (3)=1. Эту биекцию записывают как подстановку так: t= . Эту же подстановку можно короче записать как перестановку (123), что означает: 1→2→3→1. Ей соответствует граф

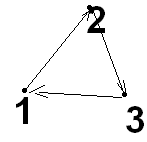
Запись (23) означает (если известно, что переставляются 3 элемента!), что 2→3; 3→2, а 1 остаётся на месте. Это соответствует подстановке . Граф этой подстановки¹ выглядит так:

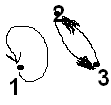
Дальнейшие примеры групп:

Множество Г всех поворотов вокруг некоторой точки плоскости. Операцией в этой группе является последовательное выполнение двух поворотов – тоже, очевидно, поворот. Эта группа абелева (от порядка выполнения поворотов результат не зависит).

Её подгруппа: все повороты на углы, кратные некоторому углу .

Все сдвиги Т плоскости. Операцией в этой группе также является последовательное выполнение двух сдвигов. Её подгруппы: сдвиги Т_а в одном направлении (вдоль какой-либо прямой а). Её подгруппы (группы Т_а): сдвиги вдоль прямой а на расстояния, кратные определённому отрезку.

Все гомотетии с рациональными коэффициентами относительно фиксированной точки плоскости. Все преобразования плоскости, порождённые симметриями относительно одной или нескольких прямых на плоскости.

Упражнение №4.

Докажите, что данное выше определение группы равносильно следующему:

Группой называется множество М c заданной на нём ассоциативной операцией  такой, что существует и при том единственное решение у каждого уравнения:

аx=b; ya=b a,bM.

Def. Отображение f:G₁→G₂ одной группы в другую называется гомоморфизмом, если выполняется f(a₁b)=f(a)₂f(b). (Разумеется, a,bG₁). Здесь ₁ – это операция в группе G₁, а ₂–операция в группе G₂.

Упражнение №5.

Докажите, что образом нейтрального элемента в G₁ при гомоморфизме явится нейтральный элемент в G₂.

Упражнение №6.

Докажите, что образом обратного к х (т.е., элемента –х в аддитивной записи) элемента группы G₁ явится элемент, обратный образу элемента х (т.е., -f(x)) в группе G₂.

Def. Множество всех прообразов нейтрального элемента группы G₂ называется ядром гомоморфизма f и обозначается как Kerf. Множество образов всех элементов G₁ (то есть, образ самой G₁) называется образом гомоморфизма f и обозначается как Imf.

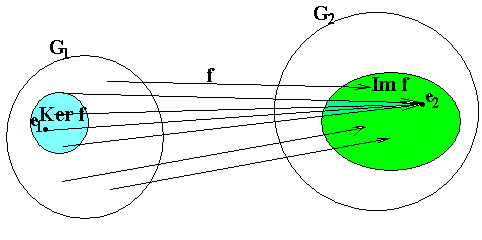
Упражнение №7.

Докажите, что Kerf – подгруппа G₁, а Imf– подгруппа G₂.

Будем пользоваться мультипликативной записью для операции в группе.

Def. Пусть Н – подгруппа группы G, аG. Рассмотрим множество аН=аh, hH. Оно называется левым смежным классом элемента а группы G по подгруппе Н.

Упражнение №8.

Левые смежные классы, взятые по всем элементам группы G, задают её разбиение на смежные классы. То есть, каждый элемент принадлежит своему смежному классу, и различные смежные классы не пересекаются (не имеют общих элементов).

Отображение а: Н→аН, а(h)=аh биективно.

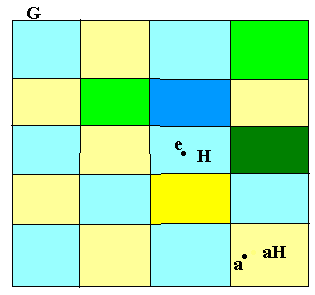
Число элементов в группе или подгруппе называется её порядком.

Упражнение №9. (теорема Лагранжа)

Порядок подгруппы конечной группы является делителем порядка группы.

Аналогично определяются правые смежные классы. В том случае, когда левые и правые смежные классы совпадают (почему именно это необходимо?) возможно естественным образом перенести операцию в группе G на смежные классы. Сделайте это в качестве упражнения. Множество смежных классов при этом превращается в группу (докажите), называемую факторгруппой группы G по подгруппе Н. Сама подгруппа Н называется в этом случае (когда левые и правые смежные классы по ней совпадают) инвариантной или нормальной или нормальным делителем. В абелевой группе, разумеется, таких проблем нет – там все подгруппы нормальны. Факторгруппа абелевой группы сама абелева.

Упражнение №10.

В конечной аддитивной группе все кратные элемента р (соответственно, степени в мультипликативной записи) не могут быть различными. Докажите, что в этом случае существует такое натуральное число m, что mр=0 (m^р=е) и при этом все предшествующие кратные р попарно различны: ipjp при 0i<jm.

Упражнение №11.

Докажите, что все эти кратные в совокупности (их будет ровно m вместе с нулём) образуют подгруппу. Порядок этой подгруппы называется порядком элемента р. Сама такая подгруппа называется циклической.

Упражнение №12.

Докажите, что любая циклическая группа – абелева.

Упражнение №13.

Докажите, что любая подгруппа циклической группы – сама циклическая.

Упражнение №14.

Докажите, что если d – делитель порядка циклической группы, то в ней существует подгруппа порядка d (теорема Лагранжа вовсе не гарантирует, что в общем случае для каждого делителя порядка группы существует подгруппа этого порядка).

Вернёмся теперь к Z и её подгруппам mZ. Поскольку Z абелева, то факторгруппа Z/mZ (а это группа знакомых уже нам остатков при делении на m по сложению!) определена. Посмотрим теперь, что происходит там по умножению: ведь мы их и умножать умеем. Попробуем найти и там подгруппу.

Ну, конечно, первым делом надо избавиться от - у него не может быть обратного. Но не только.

При m=4, например, нет и не может быть обратного у элемента . При m=6 таких (необратимых) и вовсе большинство: кроме - это . А кто является обратным к элементу ? Всё они (необратимые элементы)- это кратные делителей 6.

Упражнение №15.

Докажите, что у делителей нуля (ненулевых элементов а и b таких, что аb=0) нет обратных по умножению.

Def. Пусть две подгруппы F и K таковы, что их элементы перестановочны: f+k=k+f. Тогда можно определить сумму L=F+K как множество всевозможных сумм f+k, где первое слагаемое пробегает все элементы из F. А второе - из K.

Упражнение №16.

Докажите, что полученное множество представляет собой подгруппу. Почему понадобилось потребовать, чтобы подгруппы F и K были перестановочны?

Упражнение №17*.

Докажите, что mZ+nZ=dZ, где d=(m,n) – наибольший общий делитель m и n. (hint: take advantage of #16 and #3. First, prove that d is a common divisor of m and n. (Here you will use mZ+nZdZ, in particular, mdZ). Then prove that if some p is a common divisor m and n, then such p is necessary also is a divisor of d. Here you will use mZ+nZdZ in particular, mZ+nZd). Отсюда, в частности, следует

Упражнение №18

Если числа m и n взаимно просты, то разрешимо уравнение в целых числах: mх+nу=1.

Отсюда выводим важное утверждение:

Упражнение №19

Если простое число р делит произведение двух чисел m и n, то оно делит хотя бы одно из них.

Упражнение №20.

Обратив внимание на то, что и корень х уравнения mх+nу=1 из упражнения 18 взаимно прост с n, (то есть (х,n)=1) докажите, что все оставшиеся после выбрасывания делителей нуля элементы Z/mZ обратимы и, таким образом, образуют группу по умножению. Это попросту смежные классы взаимно простых с m элементов.

Упражнение №21. Докажите, что порядок любого элемента конечной группы является делителем порядка группы. Теперь всё готово для доказательства малой теоремы Ферма:

Упражнение №22.

Если число m не делится на простое число р, то m^р-11(modp). Более общо (Эйлер), если (m,n)=1, m<n, и (n) – функция Эйлера (число взаимно простых с n и меньших n чисел), то m^(n)1(modn).

В заключение ещё несколько упражнений на усвоение введённых понятий:

Упражнение №23.

Гомоморфизм f:G₁→G₂ инъективен тогда и только тогда, когда Kerf={e}.

Упражнение №24.

Всякая группа простого порядка – циклическая.

Упражнение №25*.

Докажите, что на самом деле в определении группы достаточно было потребовать всего лишь существования правой единицы, т.е такого элемента е, что для всех х выполняется хе=х и существования правых обратных элементов, т.е. для каждого х такого х, что хх=е. Отсюда уже будет следовать и то, что эти правые обратные служат также и левыми обратными и их единственность, и то, что единица на самом деле двусторонняя.

Def. Число левых смежных классов (если оно конечно), равное числу правых смежных классов подгруппы G по подгруппе Н, называется индексом подгруппы Н в группе G. Упражнение №26.

Докажите, что всякая подгруппа индекса 2 нормальна.

Упражнение №27.

Пусть S – некоторое подмножество группы G. Рассмотрим множество N(S) (называемое нормализатором S) состоящее из всех элементов х группы G таких, что хSх^-1 =S. Докажите, что при любом S нормализатор N(S)- подгруппа группы G.

Упражнение №28.

Теперь рассмотрим множество Z(S), (называемое централизатором S) состоящее из всех элементов х группы G таких, что хyх^-1=y yS. Докажите, что при любом S централизатор Z(S)- подгруппа группы G.