
Summer conspectus for A-group “Intellectual” Я.И.
Бесконечные последовательности, ряды и произведения1.
Под последовательностью мы понимаем любое отображение f натурального ряда в произвольное множество A. Образ этого отображения при этом становится вполне упорядоченным: на него переносится порядок из прообраза – множества натуральных чисел. Вместо записи а=f(n) пишут обычно an. Часто присоединяют ещё и ноль, так что первым элементом последовательности становится а0. Если же множество А само упорядочено, то порядок в нём, естественно, может и не совпадать с порядком следования элементов последовательности: второй элемент может оказаться меньше первого, например. Если же окажется, что он всё-таки совпадает, то есть каждый последующий элемент не меньше предыдущего, то такая последовательность называется монотонно возрастающей (неубывающей). Если каждый элемент в последовательности больше своего предшественника, то такая последовательность называется строго возрастающей. Соответственно определяются убывающие последовательности. К монотонным последовательностям относят как все возрастающие, так и все убывающие последовательности. Поскольку нам нужны будут операции, множество А будет у нас в этом конспекте, как минимум, конечномерным векторным пространством (хотя имеет смысл рассматривать в качестве А различные топологические пространства), а вообще-то чаще всего даже просто полем (например, вещественных или комплексных чисел).
Пусть f,g: - две последовательности комплексных чисел; f={f1,f2,…,fn,…}, g={g1,g2,…,gn,…}.
Упражнение 1.
Введите на множестве всех таких последовательностей операции сложения и умножения на (комплексное) число. Проверьте, что у вас получилось (бесконечномерное) векторное пространство. Назовём его l .Приведите пример какого-либо базиса в нём.
Сейчас мы введём центральное понятие всей «непрерывной математики» - понятие предела (для числовых последовательностей). Но прежде, чем дать формальное определение, обсудим его интуитивную основу. Что мы имеем ввиду, когда говорим, что некий процесс «стремится» к какому-то состоянию, какая-то точка «стремится» к какому-то положению и т.п.? Это значит, что с течением времени движущаяся точка, изменяющийся процесс, объект становятся сколь угодно близкими к некоторым стационарным состояниям.
Пусть, например, речь идёт о последовательности
действительных чисел, т.е., о
последовательности точек {an}
на вещественной прямой {an}={a1,a2,…,an,…}.
На прямой R задано
расстояние между двумя точками, равное
абсолютной величине разности их
координат: (х,у)=|x-y|.
Это позволяет говорить о близости точек
друг к другу. Теперь, если мы хотим
сказать, что наша последовательность
стремится, сходится к некоей точке а0R,
то это значит, что элементы нашей
последовательности с большими номерами
будут ближе любого наперёд заданного
расстояния от этой точки. Итак, для
любого заданного нам расстояния
найдётся номер N(),
начиная с которого все члены
последовательности будут находиться
к а0 ближе, чем на .
Теперь осталось перевести всё это с
языка русского на язык математический.
Формальное определение таково:
Def.
Последовательность {an}
в метрическом пространстве (Х, )
сходится (стремится) к
точке аХ, если
>0 N
такое, что при nN
(a,an)<.
В этом случае последовательность {an}
называют сходящейся, а точку а
называют её пределом.
Пишут:
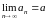 .
Последовательности, не являющиеся
сходящимися, называются расходящимися.
.
Последовательности, не являющиеся
сходящимися, называются расходящимися.
Замечания. Последовательность 1, 1.4, 1.41,…рациональных приближений 2 сходится в R (к 2), тогда как та же последовательность не является сходящейся в QR (просто потому, что 2Q). Так что сходимость зависит не только от самой последовательности, но и от того пространства, в котором она рассматривается. Определение, данное выше, легко переносится на случай общих топологических пространств. В математике часто используется термин «почти все». В применении к последовательностям, он означает «все, за исключением, быть может, конечного числа».
Упражнение 2. Проверьте, что данное выше определение сходимости может быть сформулировано и так: «>0 почти все члены последовательности находятся от а на расстоянии меньше ».
Упражнение
3.
Докажите, что последовательность
не может сходиться к двум разным точкам,
иначе говоря, ( )(
)(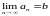 )
а=b.
)
а=b.
Напомним,
что в метрическом пространстве шаром
B(x,r)
с центром х и радиусом r
называется множество всех точек у,
расстояние от которых до центра х не
превышает r:
B(x,r)={yX|(x,y)r}.
Соответственно, сферой S(x,r)
называется множество всех тех точек
метрического пространства Х, расстояние
от которых до центра в точности равно
r: S(x,r)={yX|(x,y)=r}.
В евклидовых пространствах Еn
(n-мерных вещественных
ВП с положительно определённым скалярным
произведением) расстояние задаётся в
ортонормальном базисе с помощью координат
и теоремы Пифагора
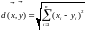 ,
а шары и сферы с центрами в нуле и
единичными радиусами называются n-мерным
шаром и (n-1)-мерной сферой
и обозначаются как Bn
(или Dn)
и Sn-1
соответственно. Множество в метрическом
пространстве называется ограниченным,
если оно содержится целиком в некотором
шаре. Любое конечное подмножество Х
ограничено (почему?).
Точка х называется
предельной для множества М, если
в любом шаре с центром в этой точке
находятся точки множества М. Приведите
пример ограниченной расходящейся
последовательности. Что представляют
собой S0 и D1?
,
а шары и сферы с центрами в нуле и
единичными радиусами называются n-мерным
шаром и (n-1)-мерной сферой
и обозначаются как Bn
(или Dn)
и Sn-1
соответственно. Множество в метрическом
пространстве называется ограниченным,
если оно содержится целиком в некотором
шаре. Любое конечное подмножество Х
ограничено (почему?).
Точка х называется
предельной для множества М, если
в любом шаре с центром в этой точке
находятся точки множества М. Приведите
пример ограниченной расходящейся
последовательности. Что представляют
собой S0 и D1?
Упражнение 4. Докажите, что любая сходящаяся последовательность ограничена (т.е., ограничено множество её значений).
Упражнение 5. Докажите, что если m – предельная точка подмножества М метрического пространства, то существует последовательность, состоящая из точек множества М, сходящаяся к m.
Упражнение 6. Вернёмся к упражнению 1. Докажите, что сходящиеся последовательности комплексных чисел образуют подпространство в l. Назовём его l 1.
Упражнение 7. Как вытекает из упражнения 3, на l 1 определён оператор lim, ставящий в соответствие каждой последовательности её предел. Покажите, что он – линейный функционал (над С).
Как вы только что доказали, операция «взятия предела», или «перехода к пределу последовательности» перестановочна с операцией суммирования: предел сумм равен сумме пределов. Проверьте теперь, что то же самое имеет место и для произведения.
Упражнение 8*.
Оператор lim коммутирует с произведением: если {fn}, {gn} l 1 и fnf; gng, то и fngnfg при n. (hint: take advantage of the identity fngn-fg=(fn-f)(gn-g)+g(fn-f)+f(gn-g))
Нетрудно установить, что и последовательность обратных величин сходится (если только эти величины определены).
Упражнение 9.
Если fnf
и f0,
fn0
ни при каких n, то
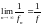 .
.
Упражнение 10.
Докажите, что операция комплексного сопряжения коммутирует с оператором lim. Пусть теперь мы имеем последовательность векторов хn в Еm, хn=(х1,n, х2,n,…, хm,n). Первый индекс указывает на номер координаты, второй – на номер вектора в последовательности. Оказывается, что сходимость векторов эквивалентна покоординатной сходимости.
Упражнение 11.
хnх={х1,х2,…,хm} xj,n хj j, 1jm
Упражнение 12.
Докажите, что сходящиеся последовательности векторов Еm образуют некоторое подпространство в ВП всех последовательностей векторов Еm и оператор lim является линейным оператором Е на Еm.
Упражнение 13.
Докажите, что оператор lim коммутирует также с действием поля R на группу Еm, а именно, если сnR, cnc а хnх, то сnхnсх.
Упражнение 14.
Докажите, что оператор lim коммутирует также и со скалярным произведением: хn®х , уn®у <xn,yn><x,y>.
Упражнение 15.
Естественно
возникает вопрос: а будет ли скалярное
произведение векторов из l
1 задаваться подобной же формулой,
т.е., всегда ли будет сходиться предел
последовательностей конечных сумм
sn=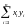 при n?
при n?
Прост, но весьма полезен следующий факт:
Упражнение 16. (теорема «о двух милиционерах»)
Если две
последовательности вещественных чисел
стремятся к одному и тому же пределу, а
третья последовательность заключена
между ними, то и она стремится к тому же
пределу: (
)(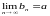 )(ancnbn)
)(ancnbn)

Также часто используется и следующее, легко доказываемое, утверждение:
Упражнение 17.
Всякая монотонная и ограниченная последовательность вещественных чисел сходится.
В большинстве случаев исследуемую на сходимость последовательность сравнивают с какой-то уже известной последовательностью и на основании, например, упражнения 16, делают вывод. Поэтому нам нужно иметь некоторый запас последовательностей, сходимость которых уже установлена. Этим мы сейчас и займёмся. Предварительно вам требуется вспомнить бином Ньютона. В следующем упражнении уже используется вещественная степень числа ху. Её мы определяли как сечение в Q, верхняя часть которого состоит из всех q>хр при всех рациональных р<y (и доказывали всё, что нужно доказывать про сечения). Вам необходимо вспомнить и это.
Упражнение 18.
Если р>0, то

Упражнение 19*.
Если р>0, то
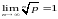
(hint:
consider separately cases p>1 and p<1. For p>1 consider
xn=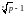 .
Then xn>0
and (1+xn)n=p)
.
Then xn>0
and (1+xn)n=p)
Упражнение
20*. 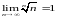
(hint:
again, take xn=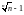 . Then 0<xn
and
n=(1+xn)n.
Now again, derive inequality from Newton’s binomial.)
. Then 0<xn
and
n=(1+xn)n.
Now again, derive inequality from Newton’s binomial.)
Упражнение 21*.
Если р>0, и
- вещественное
число, то
 .
.
(hint:
take advantage of the inequality
 and Newton’s binomial.)
and Newton’s binomial.)
Def. Последовательностью Коши, или фундаментальной последовательностью, или последовательностью, сходящейся в себе, называют последовательность {pn} в метрическом пространстве, такую, что >0 N| n.mN (pm,pn)<. В общем, расстояние между точками с большими номерами мало (становится меньше любого наперёд заданного).
Упражнение 22.
Любая сходящаяся последовательность является последовательностью Коши.
Обратное, вообще говоря, неверно. Рассмотрим, например, рациональные приближения 2. Получим последовательность рациональных чисел, которая сходится в R к 2 и потому фундаментальна. Но в Q она, оставаясь фундаментальной, не сходится (ибо в Q нет 2). Пространства, в которых всякая последовательность Коши сходится, называются полными.
Важнейшим топологическим свойством вещественной прямой и вообще всех евклидовых пространств является их полнота. Позже мы это используем, а пока что сделаем следующее
Упражнение 23.
Пусть F – подполе поля R (например, Q). Докажите, что последовательности Коши образуют подпространство FC в ВП всех последовательностей NF.
Упражнение 24.
Докажите, что последовательности, сходящиеся к нулю образуют подпространство F0 в пространстве всех сходящихся последовательностей (и, стало быть, и в пространстве всех последовательностей Коши).
Таким образом, имеет смысл говорить о факторпространстве FC/ F0.
Упражнение 25.*
Введите в нём метрику, проверьте корректность вашего определения, и докажите, что полученное вами пространство полно и линейно упорядочено.
Само F вкладывается в него естественным, “диагональным” способом: f{f,f,..}. Таким образом, получен новый способ «избавляться от дыр», более универсальный, чем способ построения вещественных чисел с помощью сечений во множестве рациональных чисел, но, видимо, более трудный для усвоения.
Def.
Пусть имеется последовательность {fn}
и n1<n2<…<nk<…Тогда
последовательность
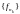 ,
k=1,2,…называется
подпоследовательностью
последовательности {fn}.
,
k=1,2,…называется
подпоследовательностью
последовательности {fn}.
Упражнение 26.
fnf каждая её подпоследовательность сходится к f.
Если же последовательность расходится, то её подпоследовательности могут сходиться к различным точкам. Предел каждой подпоследовательности называется частичным пределом исходной последовательности.
Упражнение 27*.
Постройте последовательность, множеством частичных пределов которой служит вся вещественная прямая.
Расширенной системой вещественных чисел называют вещественную прямую R вместе с добавленными к ней двумя символами, + и -. Операции с ними устроены так: -+х=- x, -х=- х>0, -х=+ х<0, ++х=+ x, +х=+ х>0, +х=- х<0,
-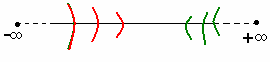 <x<+
x.
Операции между ними, а также умножение
их на ноль не определяются. Окрестностями
этих двух добавленных точек являются,
соответственно, все числа большие
какого-то числа (меньшие какого-то
числа). Таким образом, мы пишем рn+
если M
N|nN
pn>M.
Аналогично определяют -.
Def.
В расширенной системе вещественных
чисел теперь рассмотрим множество Е
всех частичных пределов последовательности
вещественных чисел {fn}.
Тогда f*=supE
и f*=infE
называются соответственно верхним
и нижним
пределом последовательности {fn}.
Обозначают это, соответственно, как
<x<+
x.
Операции между ними, а также умножение
их на ноль не определяются. Окрестностями
этих двух добавленных точек являются,
соответственно, все числа большие
какого-то числа (меньшие какого-то
числа). Таким образом, мы пишем рn+
если M
N|nN
pn>M.
Аналогично определяют -.
Def.
В расширенной системе вещественных
чисел теперь рассмотрим множество Е
всех частичных пределов последовательности
вещественных чисел {fn}.
Тогда f*=supE
и f*=infE
называются соответственно верхним
и нижним
пределом последовательности {fn}.
Обозначают это, соответственно, как
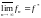 и
и
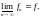 .
.
Def.
(Бесконечным) рядом
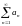 называют
последовательность {sn}частичных
сумм sn=
называют
последовательность {sn}частичных
сумм sn=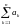 .
Бесконечным
произведением
.
Бесконечным
произведением
 называют
последовательность {sn}частичных
произведений sn=
называют
последовательность {sn}частичных
произведений sn=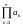 .
Итак, оба понятия являются производными
от понятия последовательности. Мы, если
не оговорено противное, предполагаем
все аnC.
.
Итак, оба понятия являются производными
от понятия последовательности. Мы, если
не оговорено противное, предполагаем
все аnC.
Опираясь на теорему о полноте вещественной и комплексной прямых, R и R2=C, докажите критерий Коши сходимости ряда:
Упражнение 28.
an
сходится >0
N|
mnN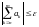 .
В частности,
.
В частности,
Упражнение 29.
an
сходится

Упражнение 30.
Ряд неотрицательных (вещественных) чисел сходится его частичные суммы образуют ограниченную последовательность.
Упражнение 31.
åan сходится, |cn|an при n>N (фиксированное число) åcn сходится.
åan расходится, сnan0åcn расходится.
Вот и пришло, наконец, время разобраться с геометрической прогрессией!
Упражнение 32.
При х1
ряд
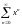 расходится,
при 0х<1 он сходится
и
=
расходится,
при 0х<1 он сходится
и
= .
.
Упражнение 33*.
Пусть неотрицательные члены ряда монотонно убывают: а1 а2 а3…0.
Тогда ряд
 сходится сходится
ряд
сходится сходится
ряд =а1+2а2+4а4+8а8+…
=а1+2а2+4а4+8а8+…
Примените предыдущие два упражнения для решения вопроса о сходимости важного ряда:
Упражнение 34.
Ряд å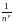 сходится при р>1 и расходится при р1.
сходится при р>1 и расходится при р1.
Расходимость
ряда å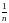 говорит нам, что условие
говорит нам, что условие
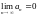 в
упр. 29 является необходимым, но не
достаточным для сходимости ряда åan.
в
упр. 29 является необходимым, но не
достаточным для сходимости ряда åan.
Def.
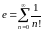 .
.
Упражнение 35. Проверьте корректность этого определения и докажите, что е<3.
Число е,
основание натуральных логарифмов и,
наряду с числом ,
важнейшая константа в математике, может
быть определена и по-другому, с помощью
другого предела. Доказательство этого
факта и важно и трудно одновременно,
поэтому дадим некоторые наводящие
соображения.
Обозначив
 и
и
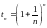 с
помощью бинома Ньютона докажите, что
с
помощью бинома Ньютона докажите, что
Упражнение
36. tnsn,
так что
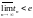 .
.
Теперь
рассмотрите
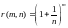 при
nm,
фиксируя (произвольное) m
и устремляя n к бесконечности,
снова, из бинома Ньютона выведите, что
при
nm,
фиксируя (произвольное) m
и устремляя n к бесконечности,
снова, из бинома Ньютона выведите, что
Упражнение
37. 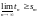 .
.
И теперь, собрав воедино оба результата, обоснуйте следующий вывод:
Упражнение 38.

Упражнение 39*.
Получите
оценку 0<e-sn<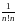 и используйте её для доказательства
того, что е – число иррациональное.
и используйте её для доказательства
того, что е – число иррациональное.
Ниже следуют два популярных признака сходимости (Коши и Даламбера), причём первый сильнее второго, но второй проще в употреблении.
Упражнение 40. (Коши)
Положим = .
Тогда при <1 ряд
åan
сходится, при >1
ряд åan
расходится, а при =1
существуют как сходящиеся, так и
расходящиеся ряды.
.
Тогда при <1 ряд
åan
сходится, при >1
ряд åan
расходится, а при =1
существуют как сходящиеся, так и
расходящиеся ряды.
Упражнение 41. (Даламбер)
Ряд åan
сходится, если
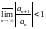 ,
расходится, если, начиная с какого-то N
,
расходится, если, начиная с какого-то N
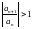 .
Существуют
как сходящиеся, так и расходящиеся ряды,
для которых
.
Существуют
как сходящиеся, так и расходящиеся ряды,
для которых
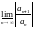 1
1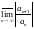 .
.
Упражнение 42.
Примените оба признака к следующим рядам и сделайте выводы:
1)
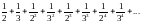
2)
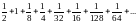
Упражнение 43*.
Для любой
последовательности положительных
чисел {сn} имеют
место неравенства:
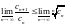 ;
;
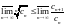 .
.
Def.
Пусть задана последовательность
комплексных чисел {сn}.
Ряд
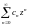 называется
степенным рядом, числа сn
– коэффициентами этого ряда.
называется
степенным рядом, числа сn
– коэффициентами этого ряда.
Применяя признак сходимости рядов Коши, докажите следующее утверждение:
Упражнение 44.
Положим =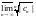 и R=
и R=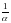 .
Если =0,
то R=+,
если a=+¥,
то R=0.
Тогда степенной
ряд
сходится, если |z|<R
и расходится, если |z|>R.
Число R называется
радиусом сходимости ряда
.
.
Если =0,
то R=+,
если a=+¥,
то R=0.
Тогда степенной
ряд
сходится, если |z|<R
и расходится, если |z|>R.
Число R называется
радиусом сходимости ряда
.
Упражнение 45.
Вычислите радиусы сходимости следующих рядов. Проанализируйте поведение этих рядов на окружности круга сходимости.
А)
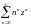 ; В)
; В)
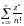 ; С)
; С)
 ; D)
; D)
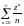 ;
; 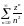 .
.
Пусть имеются
две последовательности, {an}
и {bn}.
Положим А-1=0, Аn= при
n0.
при
n0.
Упражнение 46. (формула сложения по частям)
Докажите,
что при 0pq
выполняется тождество:
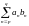 =
=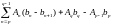
Используя этот результат и критерий Коши (не признак, а критерий!), выполните
Упражнение 47*.
Дано:
последовательность положительных чисел
b0
b1
b2…
монотонно убывает и стремится к нулю:
 ;
частичные суммы Аn
ряда an
образуют ограниченную последовательность
(т.е., ограничены в совокупности неким
число М).
Докажите, что тогда ряд åanbn
сходится.
;
частичные суммы Аn
ряда an
образуют ограниченную последовательность
(т.е., ограничены в совокупности неким
число М).
Докажите, что тогда ряд åanbn
сходится.
Примените этот результат для обоснования сходимости знакопеременного ряда:
Упражнение 48. (Leibniz)
с2m-10;
c2m0
(m=1,2,…);
|c1||c2||c3|…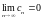 .
Тогда ряд åсn
сходится.
.
Тогда ряд åсn
сходится.
А теперь используйте предыдущий результат и формулу для геометрической прогрессии для следующего упражнения:
Упражнение 49.
Пусть радиус
сходимости ряда
равен
1 и с0с1с2…;
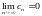 .
Тогда ряд
сходится
в каждой точке окружности |z|=1,
кроме, быть может, точки z=1.
(Вспомните про упражнение 45, D).
.
Тогда ряд
сходится
в каждой точке окружности |z|=1,
кроме, быть может, точки z=1.
(Вспомните про упражнение 45, D).
Def. Говорят, что ряд åan сходится абсолютно, если сходится ряд å|an|.
Упражнение 50.
Докажите, что абсолютно сходящийся ряд сходится.
Приведите пример неабсолютно сходящегося ряда.
Выведите отсюда усиление упр. №32: Пусть хС. Тогда ряд расходится при |х|>1, сходится, при |х|<1 и = .
Упражнение 51.
Сходящиеся ряды, так же как и последовательности, образуют ВП.
Будем умножать
ряды, как многочлены, т.е., положим сn=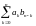 и
назовём ряд åсn
произведением рядов åan
и åbn
(произведение Коши).
и
назовём ряд åсn
произведением рядов åan
и åbn
(произведение Коши).
Пример.
Рассмотрим ряд А=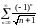 =1-(2)-1+(3)-1-(4)-1+…
=1-(2)-1+(3)-1-(4)-1+…
Упражнение 52.
Докажите,
что ряд А сходится и что А2=åсn,
где сn=(-1)n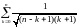 .
.
Упражнение 53*.
Докажите,
что |cn|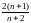 и, таким образом, ряд А2=åсn
расходится.
и, таким образом, ряд А2=åсn
расходится.
((hint:
notice
that
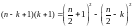 )
)
Упражнение 54** (теорема Мертенса).
Если хотя бы один из двух сходящихся рядов сходится абсолютно, то их произведение Коши сходится, причём сходится именно к произведению сумм этих рядов.
(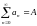 ;
;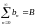 ;
сходится
абсолютно, сn=
;
сходится
абсолютно, сn=
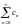 сходится
и
сходится
и
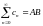 )
)
(hint:
let
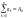 ,
,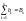 ,
,
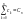 ,
n=Bn-B.
Show first, that Cn=AnB+a0n+a1n-1+…+an0
=AnB+n.
The goal is to prove, that n0.
To that end, break gn
into two separate sums, where N=N()
chose properly and fix. Then |gn
| |b0an+…+bNan-N|+|bN+1an-N-1+…+bna0|
|b0an+…+bNan-N|+
where =
,
n=Bn-B.
Show first, that Cn=AnB+a0n+a1n-1+…+an0
=AnB+n.
The goal is to prove, that n0.
To that end, break gn
into two separate sums, where N=N()
chose properly and fix. Then |gn
| |b0an+…+bNan-N|+|bN+1an-N-1+…+bna0|
|b0an+…+bNan-N|+
where =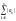 Infer from this inequality, that
Infer from this inequality, that
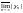 .)
.)
Пусть ряд
åсn
сходится. Тогда радиус сходимости
ряда
 равен
1 (почему?) и на интервале (-1,1) определена
функция f(x)=
.
Так вот, оказывается, что
равен
1 (почему?) и на интервале (-1,1) определена
функция f(x)=
.
Так вот, оказывается, что
Упражнение 55** (теорема Абеля).
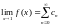
(hint:
as usual, let sn
be the partial sum c0+…+cn;
s-1=0
and s=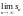 .
Show first, that
.
Show first, that
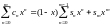 and
get from
here, that f(x)= (1-x)
and
get from
here, that f(x)= (1-x)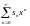 when |x|<1.
Notice,
that
(1-x)
=1
when |x|<1
and
use it to estimate |f(x)-s|
(1-x)
when |x|<1.
Notice,
that
(1-x)
=1
when |x|<1
and
use it to estimate |f(x)-s|
(1-x)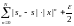 <
when x is close enough to 1.)
<
when x is close enough to 1.)
Упражнение 56*.
Всякий раз,
когда произведение двух сходящихся
рядов сходится, оно сходится именно к
произведению сумм этих рядов. (
;
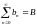 ;
;
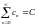 ,
где сn=
,
С=АВ)
,
где сn=
,
С=АВ)
(hint:
let f(x)=
 ,
g(x)=
,
g(x)=
 and h(x)=
.
Then f(x)g(x)=h(x)
holds true once 0x<1.
Now use Abel theorem.)
and h(x)=
.
Then f(x)g(x)=h(x)
holds true once 0x<1.
Now use Abel theorem.)
Def. Пусть k:NN – биекция, k(n)=kn. Положим а’n=ak(n). Тогда ряд åа’n называется перестановкой ряда åаn. Говорят, что ряд сходится безусловно, если все его перестановки сходятся к одной и той же сумме.
Пример.
Рассмотрим ряд
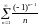 и его перестановку 1+1/3-1/2+1/5+1/7-1/4+…
Докажите, что оба ряда сходятся, но
к разным пределам.
и его перестановку 1+1/3-1/2+1/5+1/7-1/4+…
Докажите, что оба ряда сходятся, но
к разным пределам.
Упражнение 57.
Пусть åаn – неабсолютно сходящийся ряд. Положим рn=(|an|+an):2, qn=(|an|-an):2. Докажите, что оба ряда åрn и åqn расходятся.
Упражнение 58.
Продолжим в условиях предыдущего упражнения. Пусть Р1, Р2, Р3,…- неотрицательные члены этого ряда в том порядке, в котором они встречаются, а Q1, Q2, Q3,… - абсолютные величины отрицательных членов этого ряда в порядке их следования. Докажите, что оба ряда åРn и åQn расходятся.
Упражнение 59** (теорема Римана)
Пусть åаn
– неабсолютно сходящийся ряд и -+.
Тогда существует перестановка åа’n
с частными суммами s’n
такая, что
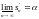 ;
;
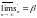 .
.
(Hint: chose two sequences converging to those limits, {n} and {n}, n<n, n ; n. Let m(1) be the first number such, that sum P1+P2+…+Pm(1) becomes greater than 1. Let k(1) be the first number such, that the algebraic sum P1+P2+…+Pm(1) – Q1-Q2-…-Qk(1) becomes less than 1. Go on with this process, find and prove that there are partial sums in this series which converge separately to both limits)
Упражнение 60.
Ряд комплексных чисел åаn сходится безусловно он сходится абсолютно.
Упражнение 61.
Если все перестановки ряда åаn сходятся, то они сходятся к одной и той же сумме.
Упражнение 62.
Последовательность {an} сходится последовательность {|an|} тоже сходится.
Верно ли обратное?
Упражнение 63.
Вычислите

Упражнение 64.
Докажите,
что последовательность {sn},
заданная рекуррентно: s1=2,
sn+1=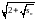 , сходится и
, сходится и
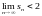 .
.
Упражнение 65.
Последовательность
{sn},
задана рекуррентно: s1=0,
 .
Найдите
её верхний и нижний пределы.
.
Найдите
её верхний и нижний пределы.
Упражнение 66.
Докажите,
что {an},
{bn}
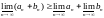 ;
;
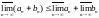 .
.
Упражнение 67.
Исследуйте на сходимость ряды åаn, в которых члены аn рядов заданы формулами:
А)
an=  ;
;
B)
an= 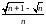 ;
;
C)
an= 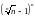 ;
;
D)
an= 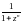 ;
z.
;
z.
Упражнение 68*.
Докажите,
что ряд åаn
сходится ряд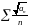 сходится (an0).
(hint:
remember
Cauchy-Bunyakovsky
inequality)
сходится (an0).
(hint:
remember
Cauchy-Bunyakovsky
inequality)
Упражнение 69*.
Докажите, что если последовательность {an} монотонна и ограничена, а ряд åbn сходится, то и ряд åаnbn сходится.
Упражнение 70.
Известно, что коэффициенты степенного ряда åаnzn – целые числа, среди которых бесконечно много отличных от нуля. Докажите, что радиус сходимости этого ряда не превышает единицы.
Упражнение 71.
Найдите
радиус сходимости каждого из следующих
рядов:
a) ån3zn; b)
 ; c)
; c)
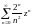 ; d)
; d)
 .
.
Упражнение 72.
Допустим,
что ряд åаn,
состоящий из положительных вещественных
чисел, расходится. Положим sn= .
Докажите, что
.
Докажите, что
А) ряды
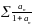 и
и
 расходятся, а ряд
расходятся, а ряд
 сходится.
сходится.
В) *Что вы
можете сказать о рядах
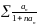 и
и
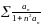 ?
?
Упражнение 73.
Теперь допустим, что ряд åаn, состоящий из положительных вещественных чисел, сходится;
Положим
rn=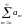 .
Докажите, что
.
Докажите, что
а) ряд
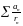 расходится, а
в)* ряд
расходится, а
в)* ряд сходится.
сходится.
Упражнение 74.
Докажите, что произведение Коши двух абсолютно сходящихся рядов сходится абсолютно.
Упражнение 75.
Пусть {an}
– последовательность, sn= и tn=
и tn= - среднее арифметическое первых n
её членов. Докажите, что сходимость anа
влечёт сходимость tnа,
однако существуют расходящиеся
последовательности, последовательности
средних арифметических которых сходятся.
Сходимость средних арифметических
расходящихся последовательностей
называется сходимостью по Чезаро.
В математике частенько употребляются
операции усреднения для «улучшения
качества» объектов.
- среднее арифметическое первых n
её членов. Докажите, что сходимость anа
влечёт сходимость tnа,
однако существуют расходящиеся
последовательности, последовательности
средних арифметических которых сходятся.
Сходимость средних арифметических
расходящихся последовательностей
называется сходимостью по Чезаро.
В математике частенько употребляются
операции усреднения для «улучшения
качества» объектов.
Augustin Louis Cauchy (21/08/1789 – 23/05/1857)
Первым осознал необходимость точных формулировок и строгих доказательств в анализе. У него также немало достижений в комплексном анализе. Именно он инициировал изучение групп перестановок. Его труды охватывают все разделы математики и математической физики и оказали огромное влияние на современников. Получил домашнее начальное образование от своего отца, закончил затем Политехническую Школу в Париже. Получив специальность инженера, уехал в Шербур, но в 1813 году вернулся в Париж и по настоянию Лагранжа и Лапласа оставил инженерное ремесло ради занятий математикой. Получив должность в Политехнической Школе, он вышел в отставку в 1830: после свержения Бурбонов он отказался давать клятву на верность новому правительству. В следующем году он занял Кафедру Математической Физики университета Турина (в то время столицы Сардинии). В 1833 свергнутый король Франции Карл Х пригласил Коши в качестве частного учителя для своего внука, герцога Бордо. В награду за службу, Карл пожаловал Коши титул барона. В1848, когда клятва на верность новому режиму была отменена, Коши вновь занял свой пост в Политехнической Школе. После переворота в 1851 году, клятва была вновь восстановлена, однако Коши был освобождён от обязанности приносить её. Его главными трудами являются «Курс анализа» 1821, «Инфинитезимальное исчисление» 1823, «Приложения инфинитезимального исчисления, Геометрия» 1826-1828, «Курс Механики», «Высшая Алгебра», «Математическая Физика».
Коши был необыкновенно продуктивен: он написал 789 статей относящихся к сходимости рядов, теории чисел, теории групп и подстановок, теории определителей, теории дифференциальных уравнений и функций. Именно он первым дал строгое доказательство формулы Тейлора и привёл её к современному виду. Большой вклад Коши внёс в механику и оптику, в теорию пластичности и упругости. Собрание его сочинений вышло в 27 томах.
Коши был убеждённым монархистом и католиком, и это создавало большие проблемы в его взаимоотношениях с коллегами. Нильс Хенрик Абель звал его «сумасшедшим католиком» Взгляды Коши были столь непопулярны среди математиков, что когда малоизвестный математик, а не Коши был избран на должность заведующего кафедрой, Коши, да и многие другие, решили, что причиной тому стали политические убеждения Коши.
Коши, как Карл Гаусс, Исаак Ньютон, Вольфганг Гёте и некоторые другие, (в отличие от многих примеров выдающихся деятелей науки и искусства) познал прижизненную славу, пользовался непререкаемым авторитетом. Репутация его, однако, омрачена приписываемой ему ролью в судьбах двух гениальнейших математиков (речь идёт об Абеле и, в особенности, об Эваристе Галуа).
Jean Le Rond d'Alembert (17/11/ 1717 – 29/10/1783)
Даламбер был незаконнорожденным, и его мать подбросила младенца на ступеньки церкви St Jean Le Rond. Ребёнок был быстро найден и отнесён в приют для сирот. Под фамилией Даламбер Жан записался в колледж. После его окончания в 1735 году, Даламбер решил заняться юриспруденцией, но его настоящим увлечением оставалась математика, которой он посвящал всё своё свободное время. В 1738 году ему было присуждено звание адвоката, но к этому времени Даламбер уже успел разочароваться в своём выборе, и решил заняться медициной. Вскоре, однако, он пришёл к выводу, что и эта профессия не для него («ещё хуже, чем теология»!). В 1740 году Даламбер представил работу о механике жидкостей, которая вызвала похвальный отзыв Клеро. В мае 1741 Даламбер был принят в Парижскую Академию Наук. Он, однако, обладал отвратительным характером и способностью ссориться со всеми окружающими. Свой знаменитый принцип в механике, носящий его имя, он обнародовал в «Трактате о Динамике» в 1743. Даламбер считал механику такой же частью математики, как Алгебру и Геометрию. Он полагал, что вся она зиждется на основных метафизических принципах, как на аксиомах, из которых все наблюдаемые физические явления могут быть выведены строго логически, как теоремы. В отличие от Клеро, который занимался в то же самое время теми же проблемами, он недооценивал роль эксперимента и нередко из-за этого приходил к выводам, противоречащим наблюдаемым эффектам. В конце концов, он перессорился со всеми академиками, и в первую очередь с Клеро, благодаря которому он в своё время в Академию и попал.
В 1744 Даламбер опубликовал «Трактат о равновесии и движении жидкостей». Эта работа содержала подход альтернативный опубликованному Даниэлем Бернулли. Даламбер считал свой метод лучшим, но Бернулли не разделял эти взгляды. В 1747 году был приглашён к редактированию, вместе с Дидро «Энциклопедию». В 1751 вышел первым том с предисловием Даламбера, оцененным обществом, как работа гения. Им написаны большинство математических статей в этом издании, состоящим из 28 томов.
Даламбер первым начал изучать дифференциальные уравнения с частными производными и их приложения к физике. Его работа «Размышления о главной причине ветров» представленная Прусской Академии наук на конкурс была удостоена приза, хотя и содержала в себе ложные физические предположения (о том, что ветры вызываются, главным образом, влиянием приливов на атмосферу, а не перепадами температур).
Эйлер оценил мощь методов Даламбера и вскоре значительно усовершенствовал их. Два математика вступили в интенсивную переписку. Вскоре, однако, их отношения испортились, потому что Даламбер посчитал, что Эйлер использует его идеи, не упоминая его при этом.
В Парижской Академии Наук Даламбер не мог публиковать свои работы, так как перессорился со всеми своими коллегами и в течение 50-х годов он посылал их в Берлинскую Академию. Однако, после того, как испортились его отношения с Эйлером, последний тоже не жаждал их публиковать. В итоге, Даламбер перестал публиковаться и там, собрал свои статьи вместе и опубликовал их отдельно в восьми томах, выходивших с 1761 по 1780. Король Пруссии Фредерик II уговаривал Даламбера принять пост Президента Академии, но Эйлер возражал. В своём письме Лагранжу Эйлер писал: «Даламбер старался мелкими придирками поставить под сомнение моё решение проблемы вибрации струны единственно по причине того, что не он решил её... Он считает, что может обмануть невежд своим красноречием. Он хотел опубликовать в нашем журнале не доказательство, а лишь утверждение о том, что моё решение неверно. Из этого вы можете понять, какая брань разразится, если он станет нашим Президентом».
Эйлер, однако, опасался напрасно, ибо, во время своего визита в 1764 к Фредерику II, Даламбер вновь отверг предложение стать Президентом и пытался убедить короля сделать Президентом Эйлера. Также отверг он и предложение Екатерины II приехать в Россию в качестве учителя для её сына Павла.
В конце жизни Даламбер больше писал на литературно-философские темы. В 1754 он был избран членом, а в1772 непременным секретарём Французской Академии и много времени посвящал редактированию некрологов.
Начиная с 1765, после целого букета заболеваний, Даламбер жаловался, что не может больше сосредоточиться на математике. В своём письме Лагранжу в 1777 он писал:
«Что раздражает меня более всего, так это то, что Геометрией, которая интересует меня более всего, я как раз и не могу заниматься. Всё что я делаю в литературе, хотя и очень хорошо принимаемое публикой, для меня есть только способ заполнить время из-за отсутствия чего-либо лучшего».
Как признанный атеист, Даламбер был похоронен в общей, безымянной могиле.
