Однородные дифференциальные уравнения первого порядка

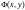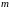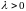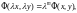Опр. Функция называется однородной функцией степени относительно переменных и , если умножение каждого из ее аргументов на одно и то же произвольное число равносильно умножению ее на , т.е. (9) где 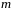- вещественное число.

Например, 1) функция 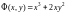является однородной функцией третьей степени относительно и , ибо

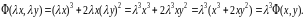
2) Функции 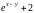однородными не являются, т.к. для них условие (9) не выполняется ни при каких .

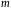3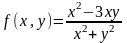 ) Проверим, является ли однородной функция

Функция однородная, нулевой степени однородности.

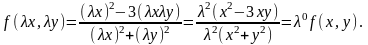
Опр. Дифференциальное уравнение 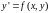(10)

называется однородным, если его правая часть 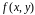есть однородная функция нулевой степени относительно своих аргументов, т.е. фактически она есть функция дроби y/x.

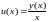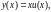Тогда обозначим , т.е. сделаем подстановку где 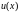- новая неизвестная функция.

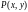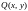Если и - однородные функции одной и той же степени, которые непрерывны в некоторой области и не обращаются одновременно в нуль ни в одной точке этой области, то дифференциальное уравнение

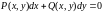
также является однородным и с помощью подстановки 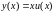приводится к уравнению с разделяющимися переменными.

Пример . Решить уравнение при 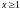. 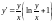(12)

Функция 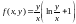определена в области 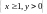, т.к. 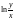имеет смысл лишь при 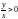. Данное уравнение является однородным

Введем подстановку 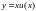, где - новая неизвестная функция. При этом 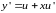.Осуществляем подстановку в уравнение (12)

:

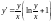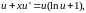
откуда следует уравнение с разделяющимися переменными

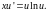
Решаем его в области :

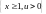Интегрируем (слева - подстановка 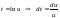) : 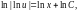где C >0. Отсюда

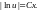
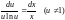
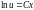, где C>0 или C<0,

т.е.

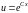
При разделении переменных считалось, что 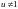. Решение 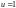получается из общего решения при .

Возвращаясь к старой переменной, получим общее решение уравнения (12) в области : где - любое число.

Пример . Для 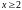найти решение уравнения 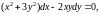(13)

удовлетворяющее начальному условию .

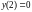У нас 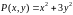, а 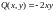. Каждая из этих функций является однородной второй степени и, кроме того, они непрерывны и не обращаются одновременно в ноль в любой области , не содержащей начала координат системы .

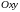Введем подстановку 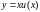, где - новая неизвестная функция 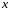. Уравнение (13) при этом имеет вид

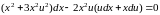или

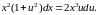
Сократим обе части уравнения на отличный от нуля множитель 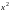и разделим переменные:

,

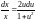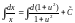
Выполняем интегрирование:

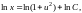где 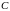- произвольное положительное число.

,

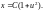
Возвращаясь к старой переменной, получим общий интеграл уравнения (13) в виде 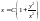или

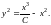
Возьмем здесь 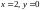, тогда

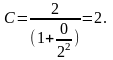
Значение подставим в общий интеграл и получим частный интеграл в виде

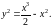
Линейные уравнения первого порядка

Опр. Дифференциальное уравнение первого порядка называется линейным, если оно может быть записано в виде 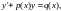(14)

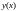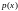где - искомая функция аргумента , а и 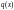- заданные непрерывные функции на промежутке .

Если 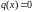всюду в 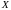, то уравнение (14) называют линейным однородным уравнением или линейным уравнением без правой части. В противном случае его называют линейным неоднородным уравнением или линейным уравнением с правой частью.