
- •Дифференциальные уравнения
- •Дифференциальные уравнения первого порядка
- •Общее, частное и особое решения.
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения первого порядка
- •Возвращаясь к старой переменной, получим общее решение уравнения (12) в области : где - любое число.
- •Линейные уравнения первого порядка
- •Метод вариации произвольной постоянной (метод Лагранжа).
- •Метод и.Бернулли.
- •Дифференциальные уравнения высших порядков
- •Дифференциальные уравнения, допускающие понижение порядка
- •Учитывая, что ,
- •Искомое частное решение имеет вид
- •Линейные дифференциальные уравнения высших порядков
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Рассмотрим линейное
неоднородное уравнение
-го
порядка
 , (42)
, (42)
где
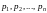 - вещественные числа, а функция
- вещественные числа, а функция
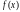 непрерывна в некотором промежутке
непрерывна в некотором промежутке
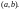
Общее решение этого уравнения может быть представлено в виде суммы общего решения соответствующего однородного уравнения и произвольного частного решения уравнения (42).
Если правая часть
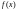 имеет специальный
вид, то
частное решение уравнения (42) можно
найти с помощью метода
неопределенных коэффициентов. Он
состоит в подстановке частного решения,
составленного по определенной формуле,
в левую часть уравнения (42) и приравнивании
коэффициентов при одинаковых степенях
имеет специальный
вид, то
частное решение уравнения (42) можно
найти с помощью метода
неопределенных коэффициентов. Он
состоит в подстановке частного решения,
составленного по определенной формуле,
в левую часть уравнения (42) и приравнивании
коэффициентов при одинаковых степенях
 в левой и правой частях
полученного равенства.
в левой и правой частях
полученного равенства.
1) Пусть
правая часть уравнения (42) имеет вид
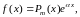 где
где
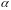 - вещественное
число, а
- вещественное
число, а
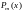 - многочлен степени
- многочлен степени
 .
.
Тогда частное решение надо
искать в виде
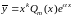 ,
,
где
 - многочлен степени
- многочлен степени
 с неопределенными коэффициентами, а
с неопределенными коэффициентами, а
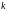 - кратность числа
- кратность числа
 как корня характеристического уравнения
однородного уравнения, соответствующего
уравнению (42) (если
как корня характеристического уравнения
однородного уравнения, соответствующего
уравнению (42) (если
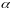 не является корнем
указанного характеристического
уравнения, то
считается равным
нулю).
не является корнем
указанного характеристического
уравнения, то
считается равным
нулю).
2) Если правая
часть уравнения (42) имеет вид
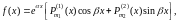
где
и
 - любые вещественные
числа, а
- любые вещественные
числа, а
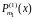 и
и
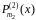 -
многочлены от
степени m1
и m2,
-
многочлены от
степени m1
и m2,
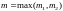 ,
то частное решение следует искать в
виде
,
то частное решение следует искать в
виде
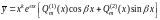 ,
,
где
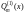 и
и
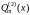 - многочлены
степени
с неопределенными коэффициентами, а
- многочлены
степени
с неопределенными коэффициентами, а
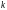 - кратность
комплексного числа
- кратность
комплексного числа
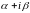 как корня характеристического уравнения
однородного уравнения, соответствующего
уравнению (42) (если
как корня характеристического уравнения
однородного уравнения, соответствующего
уравнению (42) (если
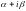 не является корнем указанного
характеристического уравнения, то
считается равным нулю).
не является корнем указанного
характеристического уравнения, то
считается равным нулю).
Пример. Решить
уравнение
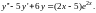
Составляем характеристическое
уравнение для соответствующего
однородного уравнения
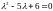
и находим его корни
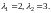 Один из корней совпадает с числом
Один из корней совпадает с числом
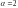 ,
значит,
,
значит,
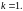 Степень многочлена
в правой части данного
уравнения m=1,
и, следовательно, частное решение следует
искать в виде
Степень многочлена
в правой части данного
уравнения m=1,
и, следовательно, частное решение следует
искать в виде
 ,
,
где
 и
и
 -неопределенные
коэффициенты. Вычислим
-неопределенные
коэффициенты. Вычислим
 и
и
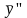 :
:
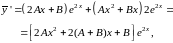
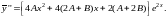
Подставляя
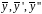 в исходное уравнение
и сокращая на
в исходное уравнение
и сокращая на
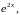 получим
получим
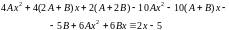
или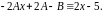
Приравнивая коэффициенты при одинаковых степенях , получим систему двух уравнений
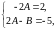 откуда
откуда
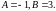
Искомое частное решение
имеет вид
 а общим решением заданного уравнения
будет
а общим решением заданного уравнения
будет
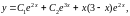 где
и
где
и
 -
произвольные постоянные.
-
произвольные постоянные.
Пример. Решить
уравнение
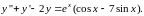
Составляем характеристическое
уравнение для соответствующего
однородного уравнения
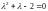
и находим его корни
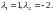 По правой части данного уравнения
находим, что
По правой части данного уравнения
находим, что
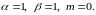 Т.к. комплексное число
Т.к. комплексное число
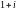 не является корнем характеристического
уравнения, то
не является корнем характеристического
уравнения, то
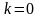 и частное решение ищем в виде
и частное решение ищем в виде

где
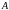 и
и
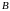 - неопределенные
коэффициенты. Вычислим вначале
- неопределенные
коэффициенты. Вычислим вначале
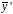 и
и
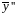 :
:
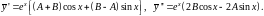
Подставив
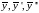 в уравнение и сократив на
в уравнение и сократив на
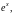 получим
получим
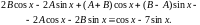
или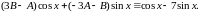
Приравнивая коэффициенты
при
 и
и
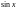 ,
получим систему двух уравнений
,
получим систему двух уравнений
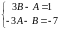 ,
откуда
,
откуда

Искомое частное решение
имеет вид
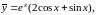 а общим решением неоднородного уравнения
будет
а общим решением неоднородного уравнения
будет
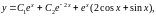 где
и
- произвольные постоянные.
где
и
- произвольные постоянные.
