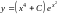- •Дифференциальные уравнения
- •Дифференциальные уравнения первого порядка
- •Общее, частное и особое решения.
- •Уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения первого порядка
- •Возвращаясь к старой переменной, получим общее решение уравнения (12) в области : где - любое число.
- •Линейные уравнения первого порядка
- •Метод вариации произвольной постоянной (метод Лагранжа).
- •Метод и.Бернулли.
- •Дифференциальные уравнения высших порядков
- •Дифференциальные уравнения, допускающие понижение порядка
- •Учитывая, что ,
- •Искомое частное решение имеет вид
- •Линейные дифференциальные уравнения высших порядков
- •Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Метод вариации произвольной постоянной (метод Лагранжа).
1)
Рассмотрим вначале однородное уравнение
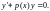 (15)
(15)
Легко видеть, что уравнение (15) является уравнением с разделяющимися переменными. Поэтому
И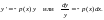 нтегрируя,
получим
нтегрируя,
получим
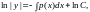 где
- произвольная положительная постоянная.
Значит,
где
- произвольная положительная постоянная.
Значит,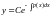 , где C
>0
или C<0.
, где C
>0
или C<0.
Утерянное при разделении переменных решение y=0 получается отсюда при C=0.
2)
Перейдем теперь к решению неоднородного
уравнения
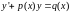 .
.
По методу Лагранжа будем искать его решение в том же виде, что и решение однородного уравнения, заменяя в нем произвольную
постоянную
некоторой, пока неизвестной, непрерывно
дифференцируемой на
 функцией
функцией
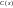 ,
т.е.
,
т.е.
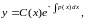 (16)
(16)
где
функцию
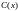 нужно выбрать так, чтобы эта функция
была решением уравнения (14) (варьируя
произвольную постоянную).
нужно выбрать так, чтобы эта функция
была решением уравнения (14) (варьируя
произвольную постоянную).
Метод и.Бернулли.
1) В согласии с этим методом будем искать решение уравнения (14)
в виде
произведения двух непрерывно
дифференцируемых на промежутке
 функций
функций
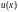 и
и
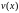 ,
одна из которых может быть выбрана по
нашему желанию, а другая определяется
с помощью самого уравнения:
,
одна из которых может быть выбрана по
нашему желанию, а другая определяется
с помощью самого уравнения: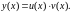 (17)
(17)
Подставив
(17) в (14), получим (опуская аргумент
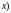
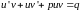 или
или
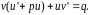
2)
Выберем функцию
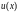 так, чтобы коэффициент при
так, чтобы коэффициент при
 (т.е. выражение, стоящее в круглых скобках)
равнялся нулю
(т.е. выражение, стоящее в круглых скобках)
равнялся нулю
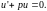
Данное уравнение сходно с уравнением (15) и его общее решение имеет вид
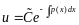 В
частности, при
В
частности, при
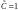
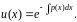
3) Подставим найденную функцию u(x) в уравнение (18)
и
получим уравнение для определения
функции
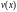
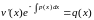 Тогда
Тогда
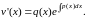
Поэтому
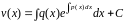 ,
где
,
где
 - произвольная постоянная.
- произвольная постоянная.
4)
Наконец, подставим значения
 и
и
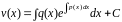 в (17).
в (17).
Пример
.
Решить уравнение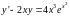 (19)
(19)
для
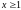 двумя методами: Лагранжа и Бернулли.
двумя методами: Лагранжа и Бернулли.
1.
В согласии с методом
Лагранжа
рассмотрим сначала однородное уравнение
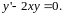
Разделяем
переменные: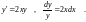
Выполняя
интегрирование, получим общее решение
уравнения (19)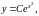 (20)
где
- произвольная постоянная.
(20)
где
- произвольная постоянная.
По
методу Лагранжа будем искать решение
неоднородного уравнения (19) в виде (20),
но вместо произвольной постоянной
возьмем некоторую непрерывно
дифференцируемую функцию
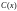 :
: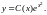 (21)
(21)
Подставим
(21) в уравнение (19):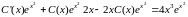 ,
,
откуда
следует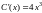 ,
тогда
,
тогда
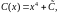
где
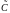 - произвольная постоянная. Подставив
это выражение в (21), получим общее решение
уравнения (19) на плоскости
в виде
- произвольная постоянная. Подставив
это выражение в (21), получим общее решение
уравнения (19) на плоскости
в виде
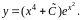
2.
Следуя методу
И.Бернулли,
будем искать решение уравнения
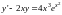 (19)
(19)
в виде
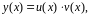 (22)
(22)
где
и
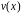 - непрерывно дифференцируемые функции.
Подставив (22) в (19), получим
- непрерывно дифференцируемые функции.
Подставив (22) в (19), получим
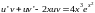 Или
Или
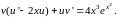 (23)
(23)
Выберем
функцию
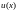 так, чтобы коэффициент при
так, чтобы коэффициент при
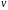 равнялся тождественно нулю, т.е.
равнялся тождественно нулю, т.е.
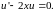
Найдем общее решение этого уравнения:
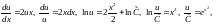
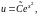 где
где
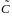 - произвольная постоянная. Положив
- произвольная постоянная. Положив
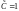 ,
найдем частное решение
,
найдем частное решение
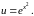 (24)
(24)
Подставим
его в уравнение (23):
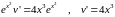 ,
,
откуда
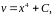 (25)
где
(25)
где
 - произвольная постоянная. Подставляя
(24) и (25) в (22), получим то же самое решение,
что и по методу Лагранжа:
- произвольная постоянная. Подставляя
(24) и (25) в (22), получим то же самое решение,
что и по методу Лагранжа: