6.Напряженность поля для различных конфигураций его источника.

Теорема Гаусса часто позволяет найти напряженность поля гораздо более простыми средствами, чем с использованием формулы (5) для напряженности поля точечного заряда и принципа суперпозиции полей.

Введем определения:

Объемная плотность заряда определяется по аналогии с обычной плотностью следующим образом:

где q – заряд, заключенный внутри малого объема V.

Поверхностная плотность заряда:

где q – заряд, находящийся на элементе поверхности S.

Линейная плотность заряда:

где q – заряд, находящийся на отрезке цилиндрического тела, имеющем длину l

С использованием теоремы Гаусса получим значения напряженностей для ряда часто используемых случаев распределения зарядов.

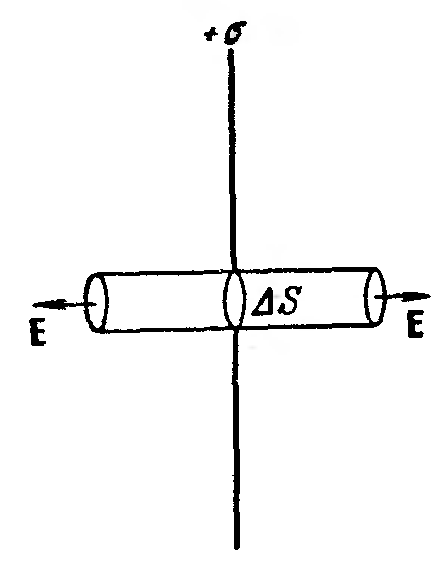
1. Поле бесконечной однородно заряженной плоскости. Плоскость заряжена с постоянной поверхностной плотностью ; для определенности будем считать заряд положительным. Из соображений симметрии: Е в любой точке поля перпендикулярна к плоскости. В самом деле, поскольку плоскость бесконечна и заряжена однородно (т. е. с постоянной плотностью), нет никаких оснований к тому, чтобы сила, действующая на пробный заряд,

Рис. 12

отклонялась в какую-либо сторону от нормали к плоскости.

Очевидно, что в симметричных относительно плоскости точках Е одинакова по величине и противоположна по направлению.

Введем в рассмотрение цилиндрическую поверхность с образующими, перпендикулярными к плоскости и основаниями величины S, расположенными относительно плоскости симметрично (рис. 12). Применим к этой поверхности теорему Гаусса. Поток через боковую часть поверхности будет отсутствовать, поскольку Е_n в каждой ее точке равна нулю. Для оснований Е_n совпадает с E. Следовательно, суммарный поток через поверхность будет равен 2E S. Внутри поверхности заключен заряд S. Согласно теореме Гаусса должно выполняться условие

откуда

(8.5)

Полученный нами результат не зависит от длины цилиндра. На любых расстояниях от плоскости напряженность поля одинакова по величине.

Рис. 13.

Рис. 14.

Картина линий напряженности выглядит так, как показано на рис. 13. Для отрицательно заряженной плоскости результат будет таким же, лишь направление вектора Е и линий напряженности изменится на обратное.

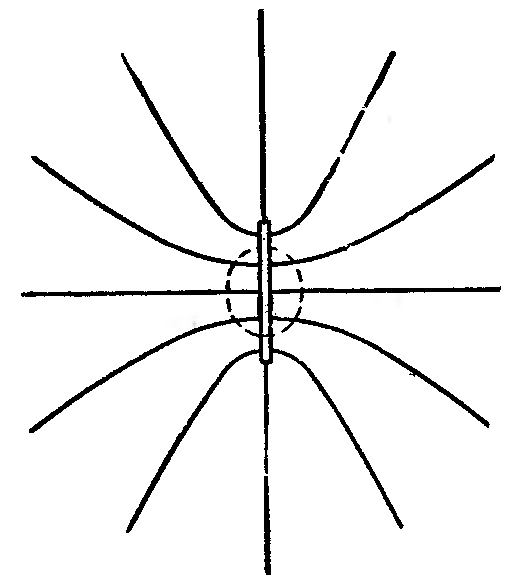
Если плоскость конечных размеров (заряженная тонкая пластинка), полученный выше результат будет справедливым лишь для точек, расстояние которых от края пластинки значительно превышает расстояние от самой пластинки (на рис. 14 область этих точек обведена пунктирной кривой). По мере удаления от плоскости или приближения к ее краям поле будет все больше отличаться от поля бесконечной заряженной плоскости. На больших расстояниях, значительно превышающих размеры пластинки, создаваемое ею поле можно рассматривать как поле точечного заряда.

2. Поле двух разноименно заряженных плоскостей.

Поле двух параллельных бесконечных плоскостей, заряженных разноименно с одинаковой поверхностной плотностью , можно найти как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями (рис. 15) складываемые поля имеют одинаковое направление, так что результирующая напряженность равна

(8.6)

Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю.

Таким образом, поле сосредоточено между плоскостями. Напряженность поля во всех точках этой области одинакова по величине и по направлению. Поле, обладающее такими

Рис. 15.

Рис. 16.

свойствами, называется однородным. Линии напряженности однородного поля представляют собой совокупность параллельных равноотстоящих прямых.

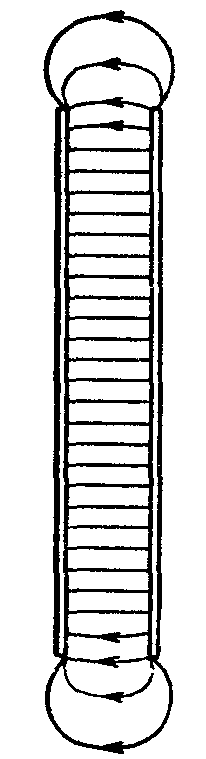
Полученный результат приближенно справедлив и в случае плоскостей конечных размеров, если расстояние между плоскостями значительно меньше их линейных размеров (плоский конденсатор). В этом случае заметные отклонения поля от однородности и величины напряженности / ₀ наблюдаются только вблизи краев пластин (рис. 16).

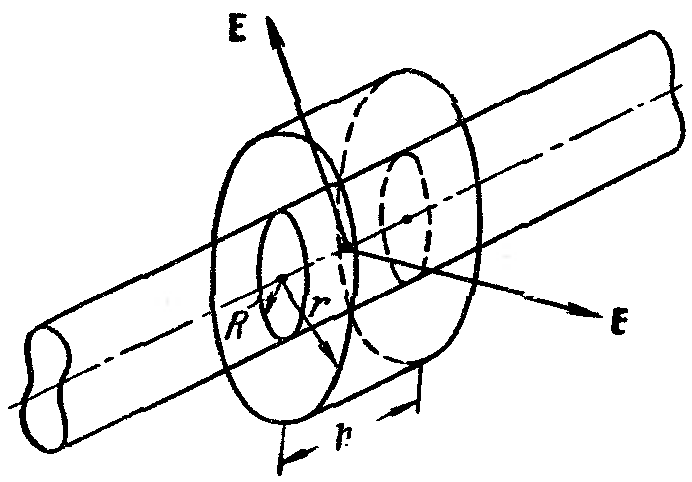
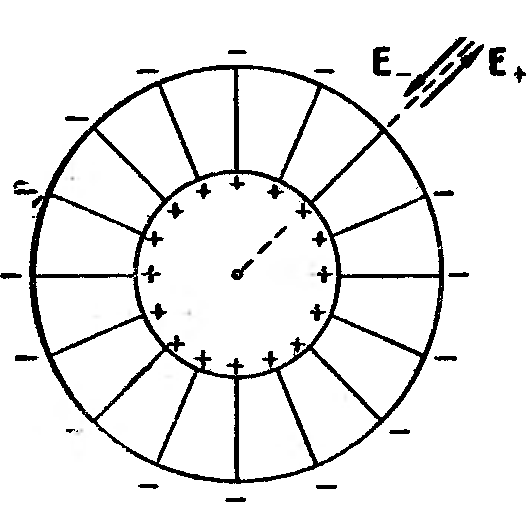
3. Поле бесконечного заряженного цилиндра. Имеем бесконечную цилиндрическую поверхность радиуса R, заряженную с постоянной поверхностной плотностью . Из соображений симметрии следует, что напряженность поля в любой точке должна быть направлена вдоль радиальной прямой, перпендикулярной к оси цилиндра, а величина напряженности может зависеть лишь от расстояния r от оси цилиндра.

Рис. 17.

Используем коаксиальную с заряженной поверхностью замкнутую цилиндрическую поверхность радиуса r и высоты h (рис. 17). Для оснований этого цилиндра Е_n = 0, для боковой поверхности E_n = E(r) (заряд считаем положительным). Поток линий Е через эту замкнутую поверхность будет равен E(r)2rh. Если r>R, внутри поверхности имеется заряд q = h, где  – линейная плотность заряда. Применяя теорему Гаусса, получаем

откуда

()

Если r < R, рассматриваемая замкнутая поверхность не содержит внутри зарядов, вследствие чего Е(r) = 0.

Таким образом, внутри заряженной цилиндрической поверхности бесконечной длины поле отсутствует. Напряженность поля вне поверхности определяется линейной плотностью заряда  и расстоянием r от оси цилиндра. Поле отрицательно заряженного цилиндра отличается от поля цилиндра, заряженного положительно, направлением вектора Е.

Из формулы (8.8) следует, что, уменьшая радиус цилиндра R (при неизменной линейной плотности заряда ), вблизи поверхности цилиндра можно получить очень сильное поле, т. е.

Рис. 18.

поле с очень большой напряженностью Е.

Учтя, что  = 2 r, для напряженности в непосредственной близости от поверхности (r = R) в соответствии с (8.8) получаем

С помощью принципа суперпозиции легко найти поле двух коаксиальных цилиндрических поверхностей, заряженных с одинаковой по величине, но отличающейся знаком линейной плотностью  (рис. 18). Внутри меньшего и вне большего цилиндров поле отсутствует. В зазоре между цилиндрами величина напряженности поля определяется формулой (8.8). Это справедливо и для цилиндрических поверхностей конечной длины, если зазор между поверхностями значительно меньше их длины (цилиндрический конденсатор, коаксиальный кабель). Заметные отступления от поля поверхностей бесконечной длины будут наблюдаться вблизи краев цилиндров.

4. Поле заряженной сферической поверхности. Поле сферической поверхности радиуса R, заряженной с постоянной поверхностной плотностью , будет, очевидно, характеризоваться центральной симметрией.

Это означает, что направление вектора Е в любой точке проходит через центр сферы, а величина напряженности является функцией расстояния r от центра сферы.

Вообразим сферическую поверхность радиуса r. Для всех точек этой поверхности Е_n = Е(r). Если r>R, внутрь поверхности попадает весь заряд q, создающий рассматриваемое поле. Следовательно,

откуда

()

Сферическая поверхность радиуса r, меньшего, чем R, не будет содержать зарядов, вследствие чего для r < R получается Е(r) = 0.

Таким образом, внутри сферической- поверхности, заряженной с постоянной поверхностной плотностью , поле отсутствует. Вне этой поверхности поле имеет такой же вид, как поле точечного заряда той же величины, помещенного в центре сферы.

Заменив в (8.10) q через 4r² и положив r = R, получим для напряженности поля вблизи заряженной сферической поверхности

(8.11)

[ср. с формулой (8.9)].

Поле двух концентрических сферических поверхностей (сферический конденсатор), несущих одинаковые по величине и противоположные по знаку заряды +q и –q, сосредоточено в зазоре между поверхностями, причем величина напряженности поля в этом зазоре определяется формулой (8.10).

5. Поле объемно заряженной сферы. Рассмотрим сферу радиуса R, заряженную с постоянной объемной плотностью . Поле такой сферы, очевидно, обладает центральной симметрией. Легко видеть, что для поля вне сферы получается тот же результат [в том числе и формула (8.10)], что и в случае поверхностно заряженной сферы. Однако для точек внутри сферы результат будет иным. Сферическая поверхность радиуса r (r < R) заключает в себе заряд, равный .

Теорема Гаусса для такой поверхности запишется следующим образом:

Так как получаем

(8.12)

Таким образом, внутри сферы напряженность поля растет линейно с расстоянием r от центра сферы. Вне сферы напряженность убывает по такому же закону, как и у поля точечного заряда.