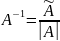15.Метод Крамера.

x=A^-1B= = =

∆ ∆ ∆

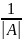
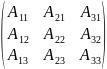
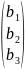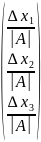
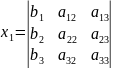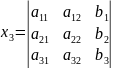
10.Парабола.

П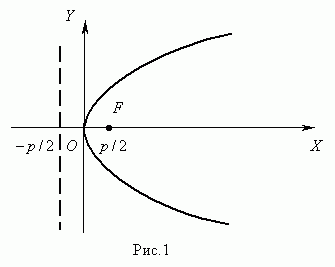 араболой называется геометрическое место точек плоскости,

равноудалённых  от заданной точки  F (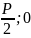 ), называемой 

фокусом параболы, и данной прямой х= - , не проходящей

через эту точку и называемой директрисой параболы.

Уравнение параболы : y ² = 2 p x .

 

Здесь ось ОХ  является осью симметрии параболы.

 

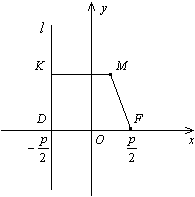
Пусть расстояние между фокусом F  и директрисой lпараболы равно p . Тогда в

выбранной системе координат парабола имеет уравнение y²=2px

Доказательство.     В выбранной системе координат фокусом параболы служит

точка F(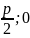 )  , а директриса имеет уравнение x=  .

Пусть M(x;y)   -- текущая точка параболы. Тогда находим

Расстоянием от точки M до директрисы l служит длина перпендикуляра MK,

опущенного на директрису из точки M. MK= x+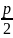 .Тогда по определению параболы 

MK=FM , то есть

→ →

y²=2px

11.Уравнение плоскости.

Общее уравнение плоскости: Ax+By+Cz+D=0

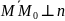
(x )

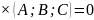
A(x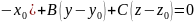

Ax+By+Cz=A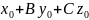

Ax+By+Cz+D=0

1.Если D=0,то плоскость имеет ур-е Ax+By+Cz=0 и проходит через начало координат.

2.Если А=0,то By+Cz+D=0→плоскость параллельна оси Ох.

3.Если А=0 и D=0,то By+Cz=0→плоскость проходит через Ох.

4.Если А=0 и В=0,то Cz+D=0→плоскость параллельна XOy.

5.Если А=0,В=0,D=0,то плоскость совпадает с XOy.

Уравнение плоскости в отрезках на осях:

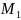(a;0;0) (0;b;0)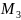 (0;0;c)

Ax+By+Cz+D=0

Aa+D=0 Bb+D=0 Cc+D=0

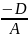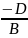a= b= c=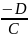

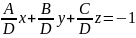
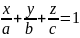
14.Свойства определителей.

1.При перестановке местами 2х параллельных строк или столбцов определитель

меняет знак.

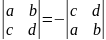ad-cb= - (cb- ad)

2.Определитель, который содержит 2 одинаковых строки или столбца, =0

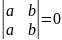ab-ab=0

3.Если определитель содержит 0ую строку или столбец, то он=0.

4.Если в определителе каждый элемент строки или столбца умножить на одно и

то же число, то получится определитель, равный исходному. умноженному на это

число.

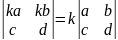
kad-kbc=k(ad-bc)

k(ad-bc)=k(ad-bc)

5.Если в определителе строка или столбец представлен в виде суммы, то этот

определитель равен сумме 2х определителей. В 1ом берется 1е слагаемое, а во

2ом – 2е.

=

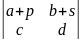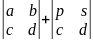
(a+p)d-(b+s)c=ad-bc+pd-cs

ad+pd-bc-cs=ad-bc+pd-cs

6.Если в определителе к строке или столбцу прибавить др. строку или столбец,

умноженный на число, то определитель не изменится.

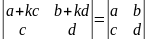
ad+kcd-bc-kcd=ad-bc

ad-bc=ad-bc

7.Т.Лапласа:Определитель квадратной матрицы равен сумме произведений

элементов строки или столбца на их алгебраическое дополнение.

8.Сумма произведений элементов какой-либо строки или столбца на алгебраи

ческое дополнение другой строки или столбца =0

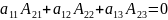
9.Определитель произведения 2х матриц равен произведению определителей

этих матриц.

16.Операции над матрицами.

1.Умножение матрицы на число.

Чтобы умножить матрицу на число k, нужно каждый элемент матрицы умножить на число k.

2.Сложение матриц.

Складываются только матрицы одной размерности. Суммой матриц А=( ) и В=( ) наз-ся

матрица С=(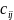 ),элементы которой равны суммам соответствующих элементов матриц Аи В,

т.е. 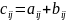при любых i и j.

Свойства:

1.А+В=В+А

2.А+(В+С)=(А+В)+С

3.А(k+l)=Ak+Al

4.(A+B)k=Ak+Bk, где А,В,С – матрицы, k,l – числа.

3.Умножение матриц.

Произведение матрицы А на матрицу В определено только в том случае, когда число столбцов

матрицы А равно числу строк матрицы В.В результате умножения получаем матрицу АВ, у

которой столько же строк, сколько их в матрице А, и столько же столбцов, сколько их в матрице В.

AB≠BA

4.Транспонирование матрицы.

Если в матрице поменять строки и столбцы, получается транспонированная матрица.

5.Элементарными преобразованиями для матриц яв-ся следующие: перестановка строк,

умножение элементов строки или столбца на число, прибавление к элементам строки или

столбца элементов др. строки или столбца. После выполнения таких преобразований матрицы

наз-ся эквивалентными.

17.Обратная матрица.

Обратная матрица - такая матрица, при умножении на которую исходная матрица даёт в результате

единичную матрицу E. Обратную матрицу можно найти только у квадратной матрицы, тоесть у матрицы,

у которой число строк равняется числу столбцов.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля,

и вырожденной, или особенной, если D = 0.

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы матрица А была

невырожденной.

Доказательство: Пусть матрица А имеет обратную. Тогда справедливы следующие равенства:

А^-1×А=А×А^-1=Е

А^-1×А=А×А^-1=Е

А^-1×А=А×А^-1=1→А≠0 А^-1≠0→А невырожденная

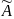- присоединенная матрица следующего вида 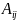- алгебраическое дополнение к

Для нахождения обратной матрицы используется следующая формула: