Ускорение точек плоской фигуры.

Теорема 4 (об ускорении точек плоской фигуры). Ускорение любой точки плоской фигуры равно векторной сумме ускорения полюса и ускорения за счет вращения фигуры вокруг полюса (оси, проходящей через полюс перпендикулярно плоскости фигуры).

.

Продифференцируем выражение (22) по времени, получим доказательство теоремы (рис. 31):

. (26)

Изменение вращательной вокруг полюса (оси, проходящей через полюс перпендикулярно плоскости фигуры) скорости _BA по времени характеризуется ускорением _BA, имеющим две составляющих: вращательное ускорение и осестремительное ускорение (Р).

Рис. 31.

Из выражений (20) и (21) следует, что:

, (рис. 31);

, (рис. 31).

Причем вектор осестремительное ускорение направлен к полюсу (точке A).

Значит, ускорение за счет вращения фигуры S вокруг полюса _BA определяется следующим образом (рис. 31):

, . (27)

Мгновенный центр ускорений плоской фигуры.

МЦУ плоской фигуры называется точка (неразрывно связанная с плоской фигурой), ускорение которой в данный момент времени равна нулю:

1. Доказательство существования мцу.

Рис. 32.

Пусть известен вектор ускорения _A некоторой точки A плоской фигуры S, угловая скорость  и угловое ускорение  вращения фигуры S вокруг этой точки (рис. 32).

Повернем вектор ускорения _A на угол в сторону углового ускорения  вращения фигуры S и проведем в этом направлении луч из точки A. На проведенном луче отложим (рис. 32) отрезок, равный: .

Из теоремы 4 определим ускорение точки Q: . Так как, согласно (27), , .

Таким образом, доказано существование МЦУ – точки Q, ускорение которой в данный момент времени равно нулю.

Единственность этой точки Q доказывается методом от противного.

2. Определение ускорений точек плоской фигуры с помощью мцу.

Рис. 33.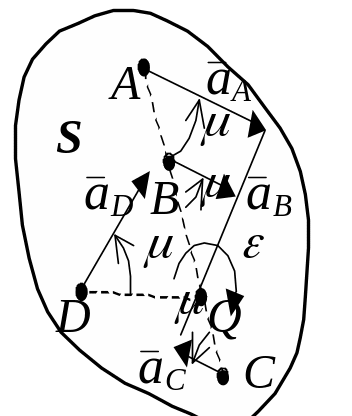

Если при определении ускорений точек плоской фигуры полюсом выбрать МЦУ этой фигуры (рис. 33), то, как следует из теоремы 4, ускорение любой точки плоской фигуры равно ускорению за счет вращения фигуры вокруг полюса. А оно в свою очередь равно сумме вращательного ускорения и осестремительного ускорения вокруг оси, перпендикулярной плоскости фигуры и проходящей через МЦУ (точку Q):

Величина ускорения точки плоской фигуры пропорциональна расстоянию от точки до МЦУ и определяется выражением:

. (28)

Вектор ускорения точки плоской фигуры _A лежит в плоскости фигуры и составляет с прямой линией, соединяющей эту точку с МЦУ, угол .

Итак, отношение ускорения любой точки плоской фигуры к расстоянию от неё до МЦУ есть величина постоянная (рис. 33) и равна из (28):

. (29)

3. Способы определения положения мцу.

3a. Пусть известен вектор ускорения _A некоторой точки A плоской фигуры S, угловая скорость  и угловое ускорение  вращения фигуры S вокруг этой точки.

В этом случае положение МЦУ определяется так, как это сделано в пункте 1 (рис. 32).

Рис. 34.

3b. Пусть известны вектора ускорения _A и _D двух точек A и D плоской фигуры S (рис. 34).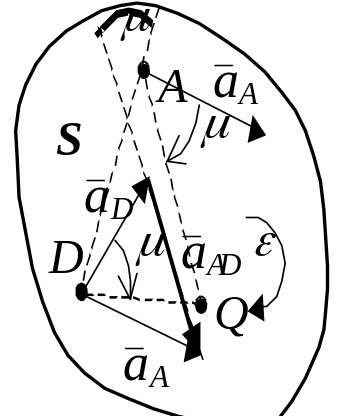

В этом случае для определения положения МЦУ прежде надо определить угол . Для этого вектор ускорения _A перенесем в точку D и построим вектор _AD (рис. 34). Угол между этим ускорением и прямой AD равен  (27). Затем проведём из точек A и D лучи, направленные под углом  к векторам ускорений этих точек в сторону направления углового ускорения . Точка пересечения этих лучей и является МЦУ плоской фигуры S (рис. 34).

3c. Пусть известны ускорения _A и _B (или _A и _C) двух точек A и B (или A и C) плоской фигуры S. Вектора этих ускорений параллельны между собой (рис. 33).

В этом случае для определения положения МЦУ надо соединить сами точки и концы векторов ускорений этих точек (рис. 33). Точка пересечения проведенных линий и является МЦУ плоской фигуры S (рис. 33).

Рис. 35.

Угол между векторами ускорений этих точек и прямой, соединяющей эти точки, будет равен . Если при построении =/2, это означает (27), что в данный момент времени =0, то есть, движение фигуры мгновенно поступательное. Если при построении =0 (рис. 35), это означает (27), что в данный момент времени =0. В этом случае для построения МЦУ надо сначала вектора ускорений повернуть в одну сторону вокруг точек на любой одинаковый угол , а затем соединить их концы (рис. 35).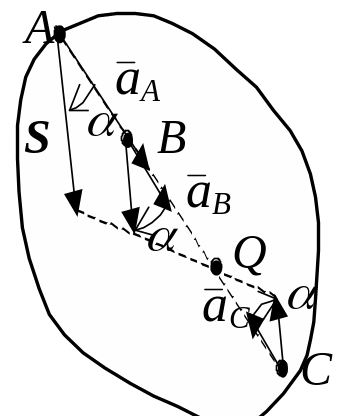

3d. Пусть известны вектора ускорений _A и _B двух точек A и B плоской фигуры S. И вектора ускорений этих точек направлены в одну сторону, параллельны между собой и равны.

В этом случае МЦУ (точка Q) плоской фигуры S находится в бесконечно удаленной точке. Тогда из (29) следует, что ==0. То есть, и угловая скорость, и угловое ускорение плоской фигуры S в этот момент времени равны нулю. Из уравнений (27) и (26) следует, что в этом случае вектора ускорений всех точек плоской фигуры S равны между собой:

.

3e. В некоторых случаях положение МЦУ удается указать из общих соображений.

Рис. 36.

Примером может являться равномерное качение диска по неподвижной поверхности. Так как скорость оси диска постоянна, значит, её ускорение равно нулю. Следовательно, МЦУ совпадает с осью. Кроме того, если диск катится без проскальзывания, то постоянна и его угловая скорость, значит, =0. Следовательно, =0. Картина распределения ускорений для этого случая приведена на рисунке 36.