Проекции вектора скорости движущейся точки.

Определим скорость точки, когда её движение задано координатным способом. Подставив выражение (3) в формулу (1), получим:

В последнем выражении производные от ортов по времени равны нулю, так как эти векторы постоянные. Не изменяется ни величина, ни направление этих векторов. Точка над буквой (координатой) означает первую производную по времени от этой величины.

Вектор скорости точки в системе координат Oxyz можно представить в виде:

.

Сравнивая последние выражения, получаем, что:

, , . (4)

Проекции вектора скорости движущейся точки равны первым производным по времени от соответствующих координат точки.

Проекции вектора ускорения движущейся точки.

Определим ускорение точки, когда её движение задано координатным способом. Подставив выражение (4) в формулу (2), получим:

В последнем выражении производные от ортов по времени равны нулю, так как эти векторы постоянные. Не изменяется ни величина, ни направление этих векторов. Две точки над буквой (координатой) означает вторую производную по времени от этой величины.

Вектор ускорения точки в системе координат Oxyz можно представить в виде:

.

Сравнивая последние выражения, получаем, что:

, , . (5)

Проекции вектора ускорения движущейся точки равны вторым производным по времени от соответствующих координат.

Естественный способ задания движения точки.

Рис. 10.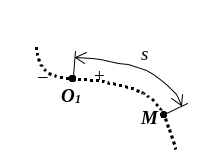

При естественном способе задания движения точки задаются:

1. траектория движения точки (рис. 10);

2. начало отсчета – точка O₁ на траектории;

3. направление отсчета ();

4. длина дуги траектории s= MO₁, определяющей положение точки M на траектории.

Если известно, как изменяется длина дуги траектории s во времени, то говорится, что движение точки M задано естественным способом:

.

Алгебраическая величина скорости движущейся точки.

Рис. 11.

Зададим движение точки и векторным и естественным способом (рис. 11). Пусть в момент времени t положение точки M определяется радиус-вектором или дугой траектории длины s. Пусть в момент времени t₁=t+t положение точки M₁ определяется радиус-вектором или дугой траектории длины s₁=s+s.

Используя (1), определим вектор скорости точки: , так как , то есть, производная радиус-вектора по длине дуги траектории равна орту касательной – вектору, направленному по касательной, модуль которого равен единице.

В результате получаем, что:

, где . (6)

Алгебраическая величина скорости точки равна первой производной по времени от длины дуги её траектории.

Если >0, то вектор скорости точки направлен в сторону положительного отсчета длины дуги траектории и – наоборот.

Связь между естественным и координатным способами задания.

Пусть движение точки M задано координатным способом:

x = x(t), y = y(t), z = z(t).

Исключая время t из этих уравнений, определяем уравнения, описывающие линию траектории точки M:

F₁(x, y, z)=0, F₂(x, y, z)=0.

Используя формулы (4), находим величину скорости точки M:

Подставляя последнее в (6), получаем:

Проинтегрировав полученное равенство по времени, устанавливаем закон изменения длины дуги траектории, выраженный через координаты движущейся точки:

.

Естественная система координат.

Рис. 12.

В любой точке пространственной линии можно ввести оси, определяющие естественную систему координат (рис. 12).

Пусть M и M₁ – две близь лежащие точки линии. и ₁ – орты, проведенные в этих точках к линии. Перенесем орт ₁ в точку M. Через два пересекающихся орта проведем плоскость. Предельное положение этой плоскости при стягивании точки M₁ в M называется соприкасающейся плоскостью к линии в точке M.

Орт , лежащий в соприкасающейся плоскости и направленный перпендикулярно орту в сторону вогнутости линии, называется ортом главной нормали к линии в точке M.

Орт , составляющий с ортами и правый базис, называется ортом бинормали к линии в точке M.

Плоскость, в которой лежат орты и , называется нормальной плоскостью к линии в точке M.

Плоскость, в которой лежат орты и , называется спрямляемой плоскостью к линии в точке M.