Применение метода Гаусса для вычисления определителей
Дана
матрица
(i,
j
= 1,2,..., n)
.
Необходимо
вычислить определитель (детерминант)
матрицы det
A
=
.
Вынесем за знак определителя ведущий элемент 1-й строки
det
A
=
, где
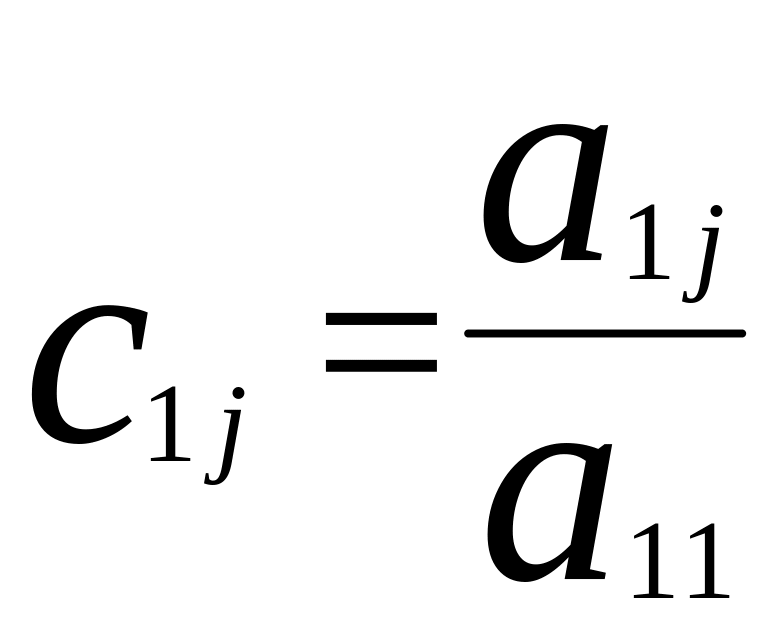( j
= 2,3,...,n
).
Вычитая первую строку , последовательно умноженную на коэффициенты
-
a21 ,
2й ,
a31 ,
3й ,
.
соответственно из
.
строк
.
.
.
.
an1 ,
nй
получим:
det
A
=
, где
.
После разложения определителя по элементам 1-го столбца имеем :
det
A
=
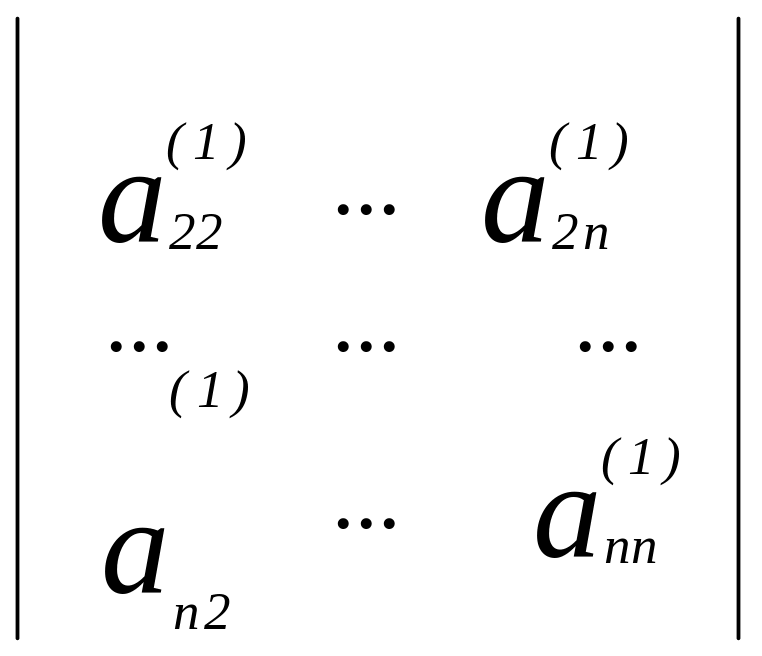- определитель (n-1)-го
порядка .
Аналогичные преобразования, приводящие к понижению порядка определителя, выполняются n раз .
В результате :
det
A=
Таким образом, при решении методом Гаусса СЛУ , можно параллельно вычислить и det A .
Замечание. Если требуется найти только det A , то вычисления производятся по схеме отвечающей прямому ходу метода Гаусса , с той лишь разницей , что отсутствуют действия над столбцом свободных членов .
Пример. Вычисление определителя матрицы (табл. 2.4).
det
A
=
Применение метода Гаусса для обращения матриц
Дана
матрица
.
Необходимо найти А -1
Если А - невырожденная (т.е. det 0 ) , то А-1 существует.
По определению: обратной называется матрица, удовлетворяющая условию AA-1 = E,
где E - единичная матрица.
E
=
.
Введем обозначение элементов искомой матрицы
А-1
=
.
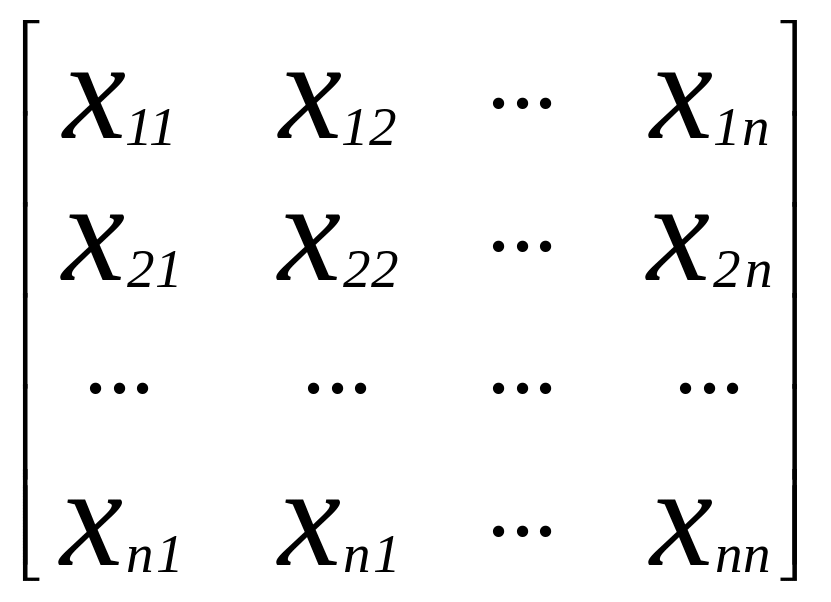Перемножим
A
на A-1
:
*
*
и т. д.
Общее количество:
уравнений – n 2 (или n систем с n неизвестными в каждой);
неизвестных – n 2.
Полученные системы , имеющие одну и ту же матрицу коэффициентов А , но различные векторы свободных членов, одновременно можно решить методом Гаусса .
Вычислительная схема:
Таблица 2.5
-
A
E
a11 a12 ...a1n
1 0 ... 0
a21 a22 ...a2n
0 1 ... 0
....................
an1 an2 ...ann
0 0 ... 1
.
.
.
.
.
.
x11 x21 ...xn1
x12 x12 ...xn2
.
.
.
x1n x2n ...xnn
Результатом является обратная матрица А-1 в транспонированном виде (табл. 2.5).
Пример. Обращение матрицы с помощью метода Гаусса (табл. 2.6).
Таблица 2.6
-
А
Е
2
1
2
1
-1
3
1
1
1
-3/2
11
5
3
3
-11/2
5
2
2
4
-5/2
1
0
0
0
-1/2
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
-1/2
-2
-1/2
-1
-1/2
-8
-5/2
-1
-1/2
-3
3/2
-1
-1/2
-1
-1/2
-1
1
0
0
2
0
1
0
0
0
0
1
0
-6
-2
-1
-1
2
-1/6
1
0
1/6
-4
-1
-2/3
1
0
1/6
0
1
0
7/3
-1
-1/3
1/7
1/3
-1/7
-1/3
1/7
1
-3/7
х1
х2
х3
х4
-2/7
2/7
5/7
-1/7
9/7
-39/14
2/7
-5/14
-1/7
9/14
-1/7
-1/14
-1/7
1/7
-1/7
3/7
Большинство распространенных методов решения СЛУ являются вариантами метода Гаусса, отличающиеся незначительными нюансами.