Метод Гаусса с выбором главного элемента

Расширенная прямоугольная матрица коэффициентов СЛУ:

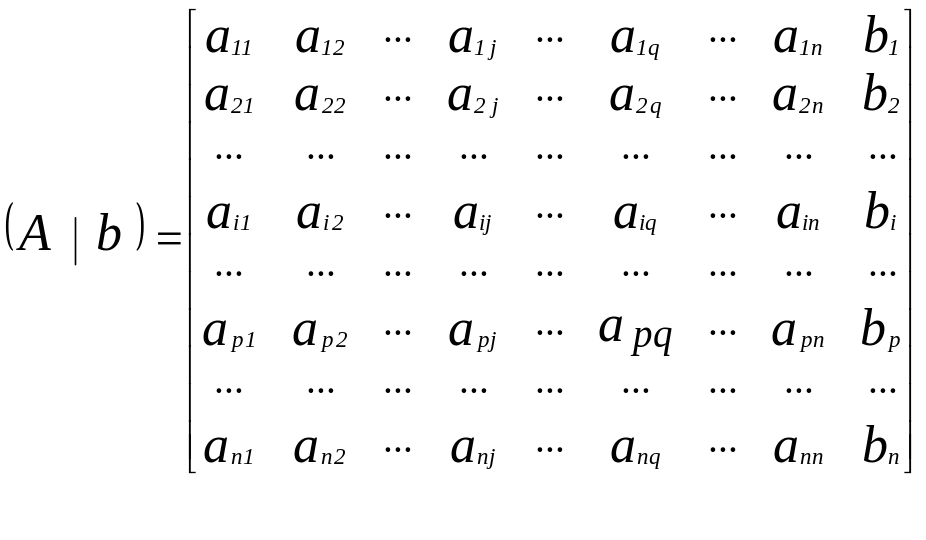
• главная строка

Прямой ход. 1. Выбор главного элемента.

Критерий выбора : a_pq = max  a_ij , ( без учёта b_i ) .

2. Вычисление множителей m_i = - .

3. Исключение неизвестной, соответствующей главному элементу

строка_i + [главная строка]  m_i .

Новая матрица A⁽¹⁾ имеет порядок (n-1)

.

.

.

В результате формируется последовательность матриц : А, А⁽¹⁾, А⁽²⁾, ..., А^(n-1),

где А^(n-1) - матрица- строка .

Обратный ход.

1. Объединение главных строк в систему.

2. Вычисление x_i .

Условие применения метода: det A  0 .

Достоинство метода менее чувствителен к ошибкам округления.

Замечания: 1. На точность метода положительно влияет критерий выбора главного элемента

( т.к. a_pq  - max , то  m_i  - min  _рез-min).

2. Простой метод Гаусса является частным случаем данного.

Пример . Решение СЛУ методом Гаусса с выбором главного элемента (табл. 2.7)

Таблица 2.7

mi		аij			bi
-1 -5/11 -3/11 -3/11	2 1 2 1	3 1 1 1	11 5 3 3	5 2 2 4	2 1 -3 -3
3/29 -7/29 -1	1/11 16/11 5/11	-4/11 2/11 2/11	- - -	-3/11 7/11 29/11	1/11 -39/11 -39/11
-4/39 -1	4/29 39/29	-10/29 4/29	- -	- -	-8/29 -78/29
	-	-14/39	-	-	0
	x1	x2	x3	x4
	-2	0	1	-1

Последовательность вычисления x_i  x₂ , x₁ , x₄ , x₃ .

Метод Гаусса–Жордана

Этап 1

1. Нормирование 1-го уравнения.

2. Исключение неизвестной х_{1 .}

Отличие. Выражение для x_k подставляется во все уравнения, кроме k-го ( с ведущим элементом ).

Этап 2

1. Нормирование 2-го уравнения.

2. Исключение неизвестной х₂.

Этап 3

1. Нормирование 3-го уравнения .

2. Исключение неизвестной х₃.

Достоинство метода  отсутствие обратного хода упрощает программирование .

Недостаток  количество действий больше , чем в простом методе Гаусса .

Пример . Решение СЛУ методом Гаусса – Жордана (табл. 2.8) .

Таблица 2.8

		aij		bi
2 1 2 1	3 1 1 1	11 5 3 3	5 2 2 4	2 1 -3 -3
1	3/2 -1/2 -2 -1/2	11/2 -1/2 -8 -5/2	5/2 -1/2 -3 3/2	1 0 -5 -4
1	1	4 1 6 -2	1 1 -1 2	1 0 -5 -4
1	1	1	1/3 5/6 1/6 7/3	-7/3 -5/6 5/6 -7/3
1	1	1	1	-2 0 1 -1	x1 x2 x3 x4