Высшая Математика КР2 5 Вариант АСОИ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет заочного и дистанционного обучения

Специальность: Автоматизированные системы обработки информации

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ № 2

Вариант № 5

Маленького Евгения Николаевича

Группа: 000622

Зачетная книжка: 000622-25

Электронный адрес: [e-mail]

Задача 45

Доказать совместность данной системы линейных уравнений и решить ее тремя методами: 1) по формулам Крамера; 2) методом Гаусса; 3) средствами матричного исчисления (с помощью обратной матрицы).

.

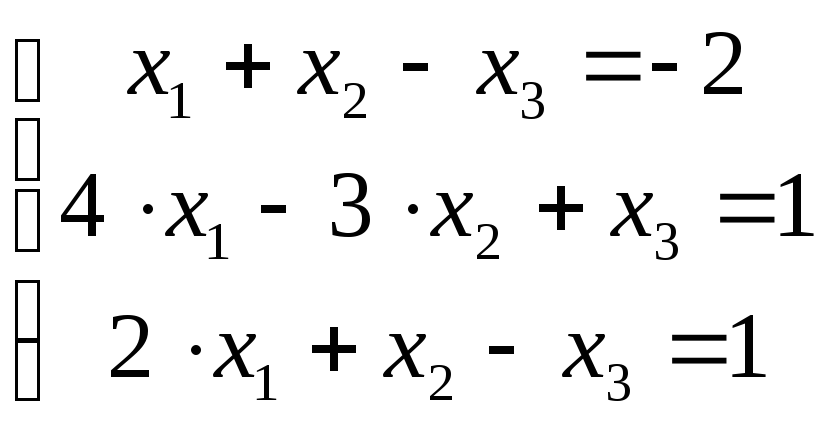Критерий Кронекера-Капелли: Для того чтобы линейная система была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы. Если же эти ранги не равны, то система несовместна.

Для того чтобы исследовать систему на совместность, применив критерий Кронекера-Капелли, составим расширенную матрицу для определения ее ранга:

;

Найдем ранг r этой матрицы с помощью элементарных преобразований, приведя ее к треугольному или трапециевидному виду. Для этого ко второй строке прибавим первую, умноженную на -4, а к третей прибавим первую, умноженную на -2. Далее к третей, умноженную на -7, прибавим вторую строку:

~ ~ ;

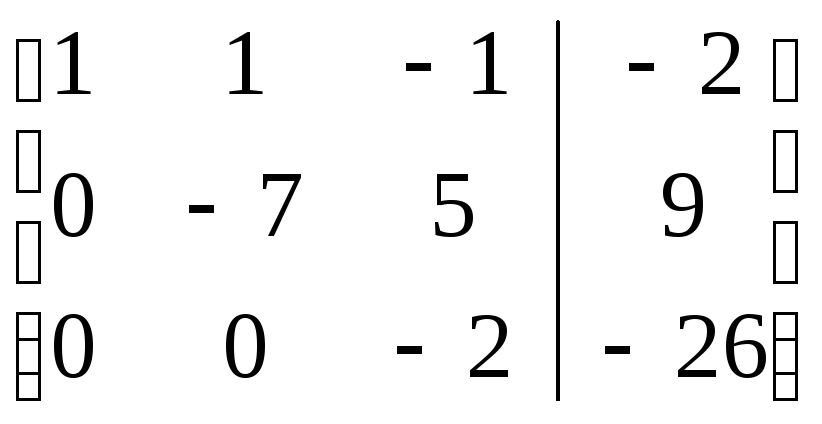Отсюда видно, что ранг расширенной матрицы равен рангу основной матрицы системы и равен количеству неизвестных n:

система совместна и имеет единственное решение.

1) Решить систему линейных уравнений с помощью формул Крамера.

Для этого найдем определитель основной матрицы системы:

;

Так как ∆≠0, то система определена, совместна и имеет единственное решение. Далее найдем определители, которые составим из главного определителя системы ∆, путем поочередной замены каждого из столбцов на столбец правой части системы:

;

;

;

Далее по формулам находим корни:

; ; .

2) Решить систему линейных уравнений методом Гаусса.

При решении системы линейных уравнений методом Гаусса действия производятся над расширенной матрицей, аналогично как мы сделали при исследовании системы на совместность:

~ ~ ;

решение системы сводится к решению эквивалентной системе линейных уравнений:

; Отсюда найдем x₃ и далее, подставляя в уравнения по восходящей, найдем x₂ и x₁:

3) Решить систему линейных уравнений матричным методом (с помощью обратной матрицы).

Решение системы линейных уравнений матричным методом находится по формуле: , где – матрица-столбец неизвестных, – обратная матрица, основной матрицы системы, – матрица-столбец правой части системы уравнений. Введем матрицы:

; ; ;

Найдем обратную матрицу по формуле:

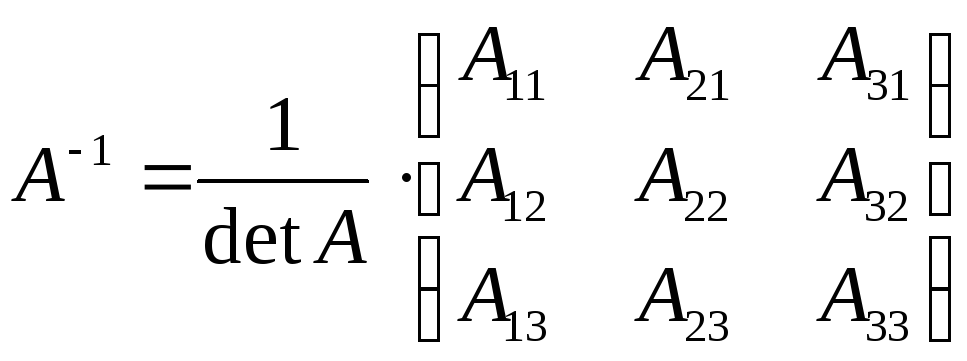, где – алгебраическое дополнение, M_ij – минор, получается путем удаления i–ой строки и j–ого столбца, det A – детерминант матрицы A, мы нашли его в пункте 1 (∆=-2), т.к. он не равен нулю, значит, обратная матрица существует:

;

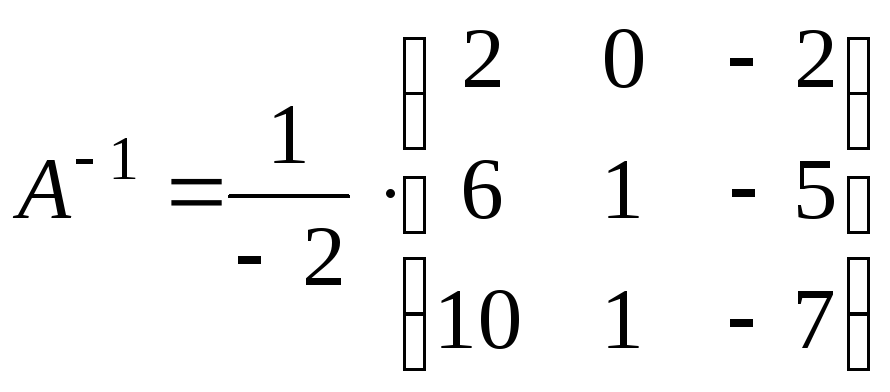Проверим правильность нахождения обратной матрицы по формуле:

, где E – единичная матрица, матрица у которой элементы на главной диагонали равны единице, а остальные – нулю:

– верно;

Задача 55

Найти общее решение системы линейных уравнений.

.

Исследуем систему линейных уравнений, применив критерий Кронекера-Капелли. Составим расширенную матрицу системы:

;

Применим элементарные преобразования:

~ ~ ;

– система линейных уравнений несовместна и решений не имеет. Также последняя строка эквивалентной матрицы, полученной путем элементарных преобразований, соответствует:

– что не верно.

Задача 65

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

.

Собственными значениями линейного преобразования, заданного в некотором базисе матрицей, являются корни характеристического уравнения матрицы. Составим характеристическое уравнение и найдем его корни:

;

;

;

– найденные корни являются собственными значениями матрицы A.

Каждому собственному значению матрицы соответствует собственный вектор.

Так при система примет вид:

;

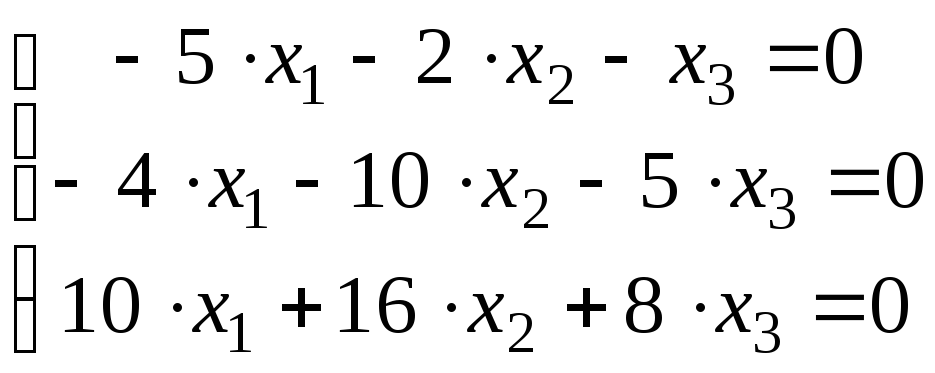
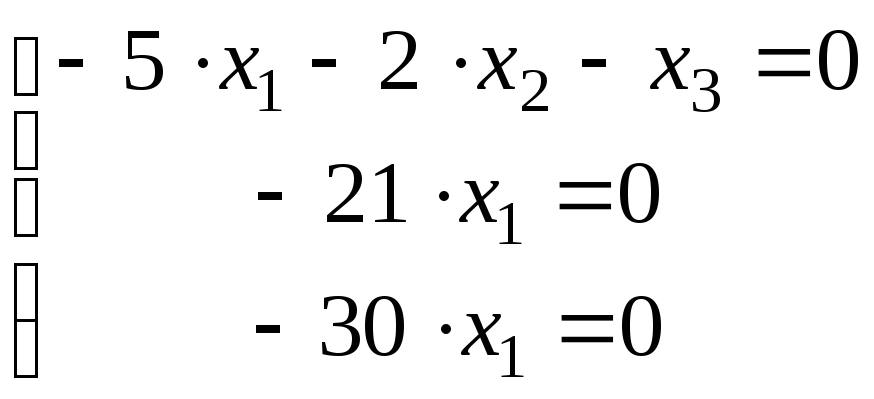
Следовательно, собственный вектор, соответствующий собственному значению , имеет вид: - где x₃ – произвольное действительное число, не равное нулю. Положив его, в частности, равным единицы, получим собственный вектор в виде ;

Аналогично при система примет вид:

;

Значит, собственному значению соответствует собственный вектор

или ;

При система имеет вид:

;

Значит, собственному значению соответствует собственный вектор

или .

Задача 75

Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка и построить ее в декартовой системе координат.

.

Составим матрицу данной квадратичной формы ;

Составим характеристическое уравнение матрицы A и найдем ее собственные значения и собственные векторы:

;

Значит, собственные векторы будут иметь вид:

для x₁ = –x₂ ;

для x₁ = x₂ ;

Нормируем собственные векторы:

; ;

Матрица перехода к новому базису будет иметь вид ;

Введем замену переменных и подставим эти выражения в исходное уравнение кривой:

; ; тогда:

;

Преобразуя полученное выражение, получим:

;

;

;

Введем еще одну замену и подставим в полученное выражение:

; ;

;

;

;

Полученное уравнение является каноническим уравнением эллипса, с центром в начале, смещенной, системы координат O''X''Y'', с полуосями и .