Высшая математика часть 1. Контрольная работа №1. Вариант 4

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Факультет заочного, вечернего и дистанционного обучения

Специальность: программное обеспечение

информационных технологий

КОНТРОЛЬНАЯ РАБОТА

ПО ВЫСШЕЙ МАТЕМАТИКЕ № 1

Вариант № 4

1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

Задание 4.

Даны четыре вектора (а1, а2, а3), (b1, b2, b3), (c1, c2, c3) и (d1, d2, d3) в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора d‾ в этом базисе.

(1,3,5), (0,2,0), (5,7,9), (0,4,16).

Базисом в пространстве являются любые три некомпланарных вектора. Условием некомпланарности трёх векторов является равенство их смешанного произведения нулю.

, = = 1*2*9+3*0*5+0*7*5 – (5*2*5+7*0*1+0*3*9) = 18 – 50 = −32 ≠ 0

Значит векторы , , некомпланарны и образуют базис.

Для того, чтобы найти разложение , составим систему уравнений в координатном виде:

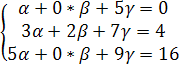
Найдём Δα, Δβ, Δγ. Определитель Δ= −32

Δα = 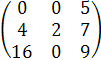= 0*2*9+0*7*16+4*0*5 – (2*5*16+0*7*0+4*0*9) = −160

Δβ = = 1*4*9+0*7*5+3*16*5 – (5*4*5+1*7*16+3*0*9) = 36+240−100−112 = 64

Δγ = = 1*2*16+0*4*5+3*0*0 – (5*2*0+0*4*1+3*0*16) = 32

Таким образом α = = = = 5

β = = = −2

γ = = = −1

Значит: = 5− 2−

Ответ: = 5− 2−

Задание 14.

Даны координаты вершин пирамиды A₁A₂A₃A₄.

Найти:

1) длину ребра А₁А₂;

2) угол между ребрами А₁А₂ и A₁A₄;

3) угол между ребром A₁A₄ и гранью A₁A₂A₃;

4) площадь грани A₁A₂A₃;

5) объём пирамиды;

6) уравнения прямой А₁А₂;

7) уравнение плоскости A₁A₂A₃;

8) уравнения высоты, опущенной из вершины A₄ на грань A₁A₂A₃. Сделать чертёж.

A₁ (2,4,3), A₂ (7,6,3), A₃ (4,9,3), A₄ (3,6,7).

Решение

1) Найти длину ребра А₁А₂

Находим координаты вектора:

= (7 – 2; 6 – 4; 3 – 3) = (5;2;0)

И соответствующая длина ребра равна:

= =

2)Найти угол между ребрами А₁А₂ и A₁A₄

Угол φ между рёбрами и вычисляем по формуле:

cos φ =

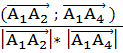
(3−2 ; 6−4 ; 7−3) = (1 ; 2 ; 4)

= =

Таким образом cos φ = = => φ = arcos

3) Найти угол между ребром A₁A₄ и гранью A₁A₂A₃

Найдём вектор ┴ () , (4−2 ; 9−4 ; 3−3) = (2 ; 5 ; 0)

= * = = − + = 21

таким образом ∟( ;^ ()) = cos ( − θ) = sin θ = = = => θ = arcsin

4) Найти площадь грани A₁A₂A₃

Площадь грани находим, используя геометрический смысл векторного произведения:

= = = = 10,5

5) Найти объём пирамиды

Объём пирамиды численно равен одной шестой модуля смешанного произведения векторов: , ,

V = = = (5*5*4+2*0*1+2*2*0 – (1*5*0+2*0*5+2*2*4)) = (100 – 16) =14

6) Найти уравнения прямой А₁А₂

Запишем уравнение прямой в каноническом виде:

= =

значит прямая расположена параллельно плоскости x0y.

Запишем уравнение прямой как линию пересечения двух плоскостей

7) Найти уравнение плоскости A₁A₂A₃

Для составления уравнения плоскости воспользуемся формулой составления по трём точкам:

= 0

– + ( = 0

(2*0 – 5*0) – (y – 4) (5*0 – 2*0) + (z – 3) (5*5 – 2*2) = 0

(z – 2) * 21 = 0 => z – 3 = 0

8) Найти уравнения высоты, опущенной из вершины A₄ на грань A₁A₂A₃. Сделать чертёж

Искомое уравнение высоты получим из канонических уравнений прямой:

=

где () принадлежит искомой прямой

m, n, p – координаты вектора , параллельного искомой прямой

В качестве точки возьмём точку (3;6;7) , а в качестве вектора возьмём нормальный вектор плоскости A₁A₂A₃ , то есть (0;0;1)

Таким образом имеем: = =

Схематический чертёж:

Задание 24.

Вычислить координаты центра окружности, описанной около треугольника с вершинами A(-1,1), B(2,-1), C(4,0).

Известно, что центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника.

Поэтому для нахождения центра окружности достаточно найти точку пересечения двух любых серединных перпендикуляров.

Найдём уравнения прямых АВ и АС; если А (–1;1) , В (2; –1) , С (4;0)

АВ: = => 2x + 3y – 1 = 0

(2;3)

АC: = => x + 5y – 4 = 0

(1;5)

Найдём координаты точек К, М, которые являются серединами сторон АВ и АС соответственно

K => K

M => M

Теперь составим два уравнения прямых серединных перпендикуляров, по точке и направляющему вектору, который совпадает с вектором нормали для соответствующих сторон треугольника

KO: = (2;3) , K

= => 3x – 2y – = 0 (1)

MO: = (1;5) , M

= => 5x – y – 7= 0 (2)

таким образом O = KO MO

решим систему уравнений (1) и (2):

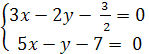
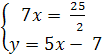
=> O ( ; ) – центр описанной окружности около ΔABC

Задание 34.

Построить на плоскости область решений системы линейных неравенств.

Для построения области решений выполним алгоритм для каждого неравенства:

1. Строим соответствующую прямую

2. Проверяем удовлетворяет ли точка (0;0) нашему неравенству => выбираем нужную область решения для данного неравенства

Таким образом данной системе неравенств удовлетворяют все точки внутри ΔАВС и на его границе.

Найдём координаты точек А, В, С.

А:

=> A (7;5)

B:

=> B (12;11)

C:

=> C (16;9)

Задание 44.

Составить уравнение линии, каждая точка которой находится вдвое ближе к точке A(1,0), чем к точке B(-2,0).

Обозначим произвольную точку искомой линии С (х;у). Тогда по условию:

2 =

так как A (1;0) , B (–2;0) , то

= =

= =

Значит:

2 =

4(­ ­− 2x + 1 + ) = ­ ­+ 4x + 4 +

3 − 12x + 3 = 0

− 4x + = 0

+ = − это уравнение окружности с центром в точке (2;0) и радиусом R = 2.