
ВМ. Контрольная 1, вариант 2
.docКонтрольная работа №1
Вариант 2
Даны четыре вектора
![]() в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы
![]() ,
,
![]() ,
,
![]() образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
![]() в этом базисе.
в этом базисе.
Решение
Составим определитель матрицы из
координат векторов
![]() ,
,
![]() ,
,
![]()
и вычислим его:
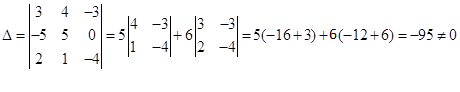
Так как Δ≠0, то векторы
![]() ,
,
![]() ,
,
![]() линейно независимы и образуют базис.
линейно независимы и образуют базис.
Получим систему уравнений
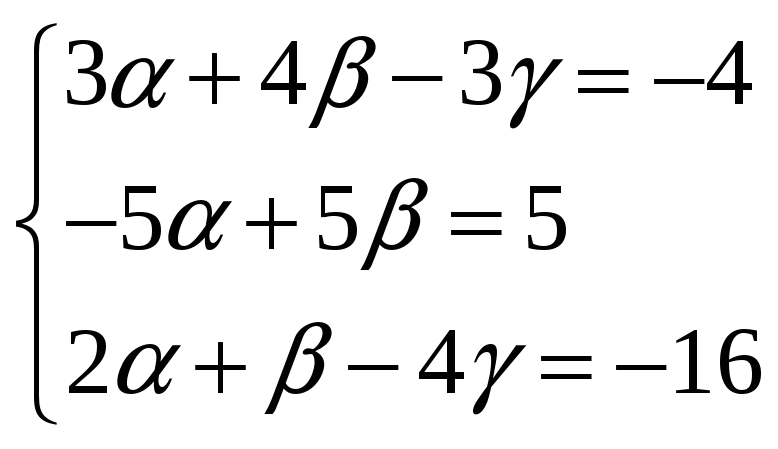
Решим систему методом Гаусса:

Полученная матрица эквивалента системе
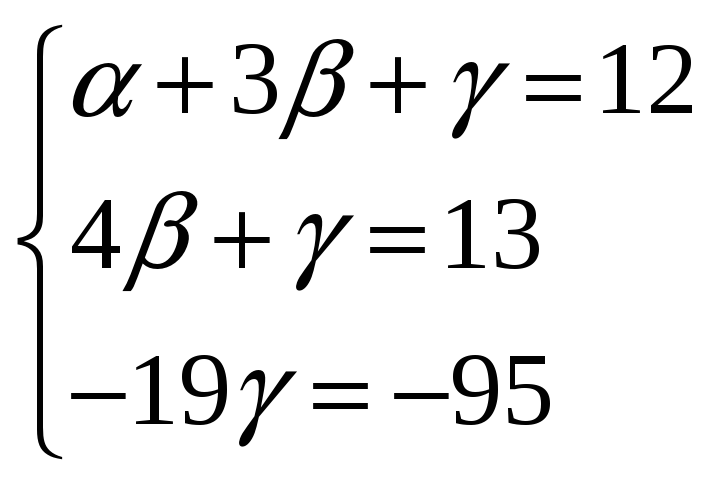
γ=![]()
β=![]()
α=![]()
Таким образом,
![]()
Ответ:
![]()
№12
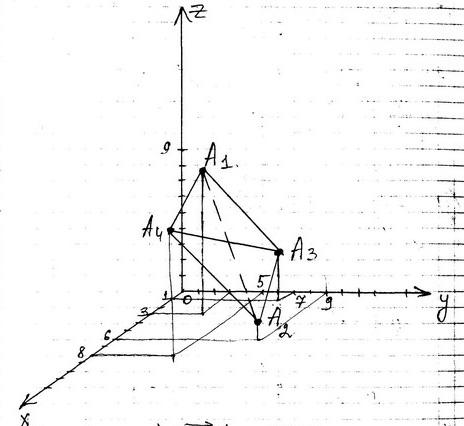
Даны координаты вершин пирамиды А1А2А3А4. Найти 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4; 3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды; 6) уравнения прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнения высоты, опущенной из вершины А4 на грань А1А2А3; Сделать чертеж.
А1 (3,3,9) А2 (6,9,1) А3 (1,7,3) А4 (8,5,8)
Решение
1) Найдем длину ребра А1А2 по формуле
![]()
![]()
2) Косинус угла между ребрами А1А2 и А1А4:
 ,
,
![]() =(x2–x1;
y2–y1;
z2–z1)=(6-3;9-3;1-9)=(3;6;-8),
=(x2–x1;
y2–y1;
z2–z1)=(6-3;9-3;1-9)=(3;6;-8),
![]() =(x4–x1;
y4–y1;
z4–z1)=
(8-3;5-3;8-9)=(5;2;-1)
=(x4–x1;
y4–y1;
z4–z1)=
(8-3;5-3;8-9)=(5;2;-1)
![]()
![]()
3) ) Синус угла между прямой А1А4 и плоскостью А1А2А3:
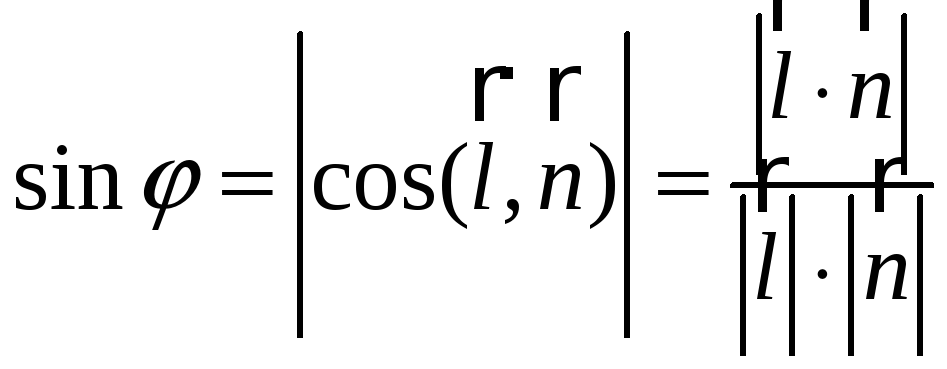 ,
где
,
где
![]() –
направляющий вектор прямой,
–
направляющий вектор прямой,
![]() –
нормальный вектор к плоскости.
–
нормальный вектор к плоскости.
![]() (5;2;-1)
(5;2;-1)
![]()
![]() =(x3–x1;
y3–y1;
z3–z1)=(1-3;7-3;3-9)=(-2;4;-6),
=(x3–x1;
y3–y1;
z3–z1)=(1-3;7-3;3-9)=(-2;4;-6),
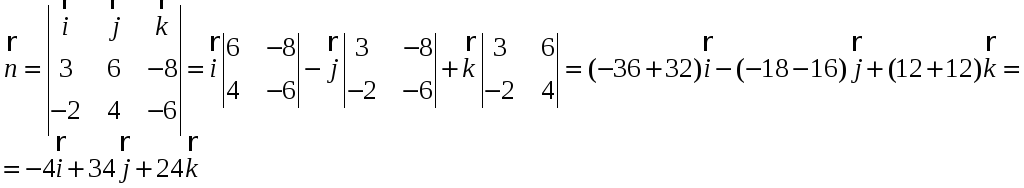
![]() =(-4;34;24)
=(-4;34;24)
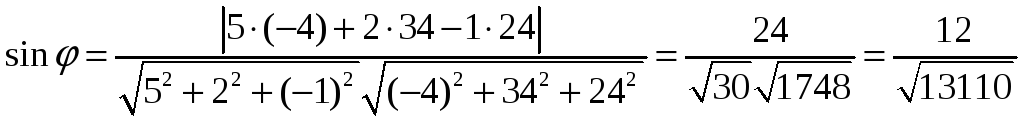
![]()
4) Найдем площадь грани А1А2А3
S=![]()
S=![]() ед2
ед2
5) Объем пирамиды найдем по формуле
V=![]()
V= ед3
ед3
6) Каноническое уравнение прямой А1А2
![]()
![]()
![]()
7) Найдем уравнение плоскости А1А2А3
![]() ,
,
где
![]() (А,В,С)–нормальный
вектор к плоскости А1А2А3,
(А,В,С)–нормальный
вектор к плоскости А1А2А3,
А1(x1,y1,z1)– координаты точки, через которую проходит плоскость.
Получим
-4(x-3)+34(y-3)+24(z-9)=0
2x-17y-12z+153=0 –общее уравнение плоскости А1А2А3
8) Найдем уравнение высоты, опущенной из точки А4, на грань А1А2А3 по формуле
![]() ,
,
так как нормальный вектор
![]() (А,В,С)
к плоскости А1А2А3
является направляющим вектором высоты.
Получим
(А,В,С)
к плоскости А1А2А3
является направляющим вектором высоты.
Получим
![]()
![]() –
каноническое уравнение прямой.
–
каноническое уравнение прямой.
Сделаем чертеж:
Ответ: 1)А1А2=![]()
![]()
![]()
4) S=![]() ед2
ед2
5) V=4ед3
6)
![]()
7) 2х-17y-12z+153=0
8)
![]()
№22
Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(3,0), чем от оси ординат.
Решение
Пусть М(x,y)– произвольная точка искомой кривой. Сделаем чертеж:
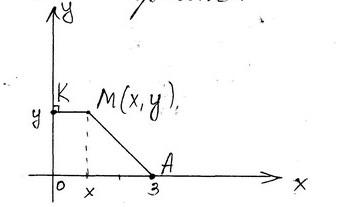
Тогда
АМ=![]()
МК=![]()
По условию АМ=2МК
Тогда составим уравнение:
![]()
Откуда
![]()
![]()
![]()
Приведем уравнение линии к каноническому виду
![]()
![]()
![]() –каноническое
уравнение гиперболы с центром в точке
(-1;0) и полуосями a=2, b=
–каноническое
уравнение гиперболы с центром в точке
(-1;0) и полуосями a=2, b=![]()
Ответ:
![]()
№32
Доказать совместность данной системы линейных уравнений и решить ее двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

Решение
Составим расширенную матрицу
![]() системы уравнений и преобразуем ее к
треугольному виду
системы уравнений и преобразуем ее к
треугольному виду
 =>
=>
![]() =3
=3
Так как rang A=rang![]() =3
и n=3 (число неизвестных),
то система уравнений совместна и имеет
единственное решение.
=3
и n=3 (число неизвестных),
то система уравнений совместна и имеет
единственное решение.
-
Решим систему методом Гаусса. Полученная матрица эквивалентна следующей системе уравнений:
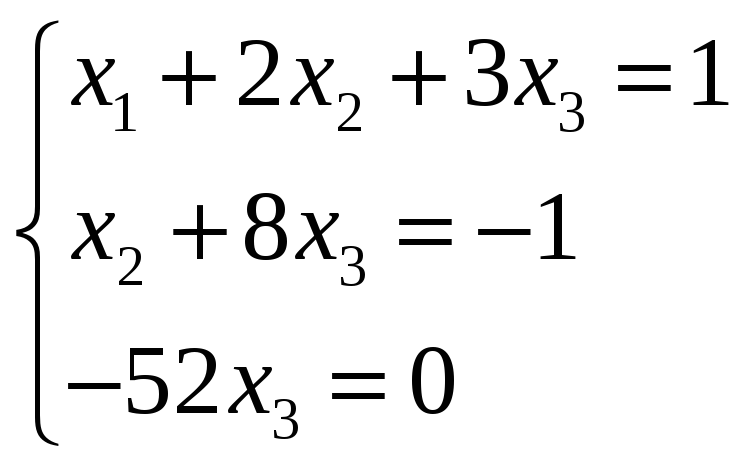 , откуда
, откуда
x3=0
x2=![]()
x1=![]()
-
Решим систему уравнений средствами матричного исчисления. Данная система эквивалентна матричному уравнению AX=B , откуда Х=
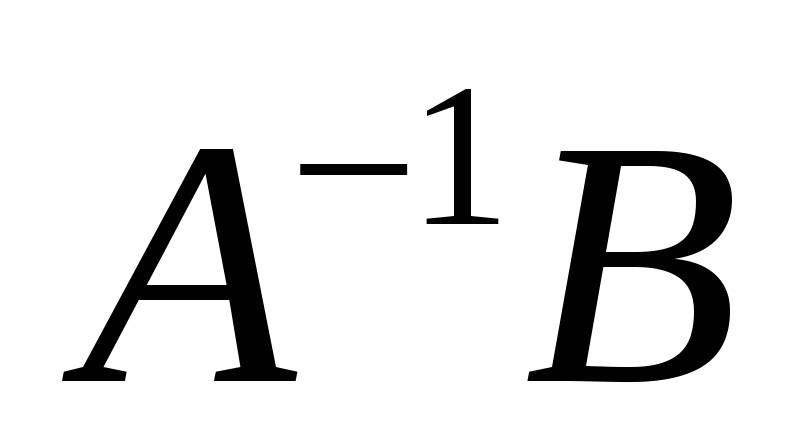 ,
,
где А=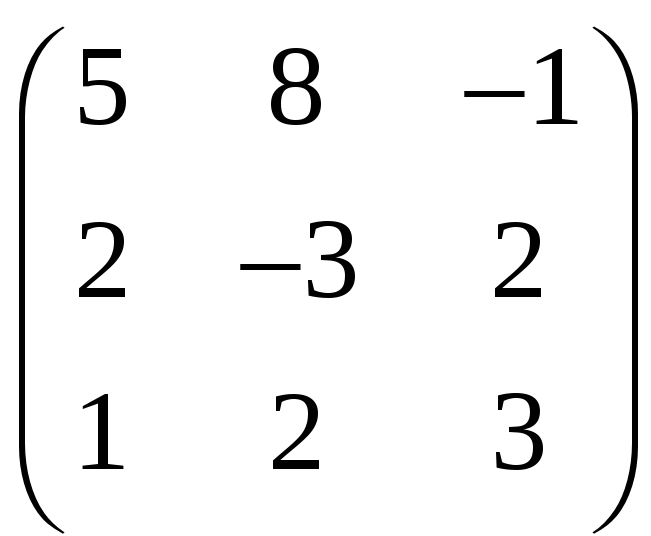 ,
Х=
,
Х=![]() ,
В=
,
В=![]()
А-1– матрица, обратная матрице к А
 ,
где Аij – алгебраические
дополнения к элементам матрицы А.
,
где Аij – алгебраические
дополнения к элементам матрицы А.
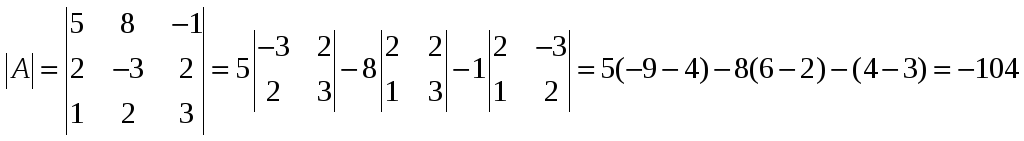
А11=![]()
А12=![]()
А13=![]()
А21=![]()
А22=![]()
А23=![]()
А31=![]()
А32=![]()
А33=![]()
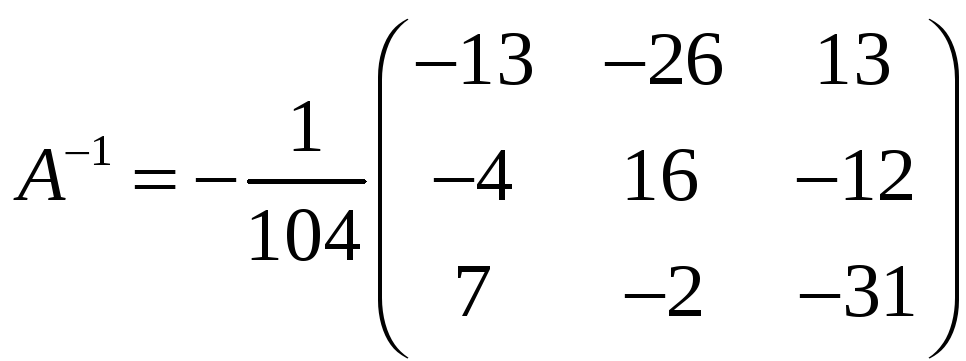
Х=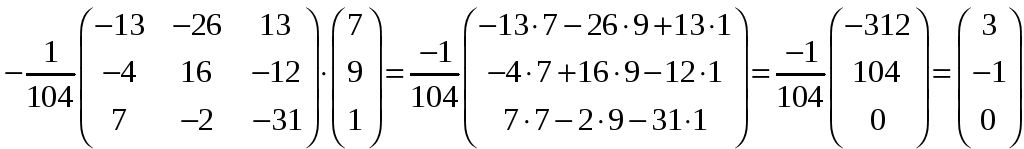 ,
,
откуда х1=3, х2=-1, х3=0
Ответ: х1=3, х2=-1, х3=0
№42
Найти размерность и базис пространства решений однородной системы линейных уравнений
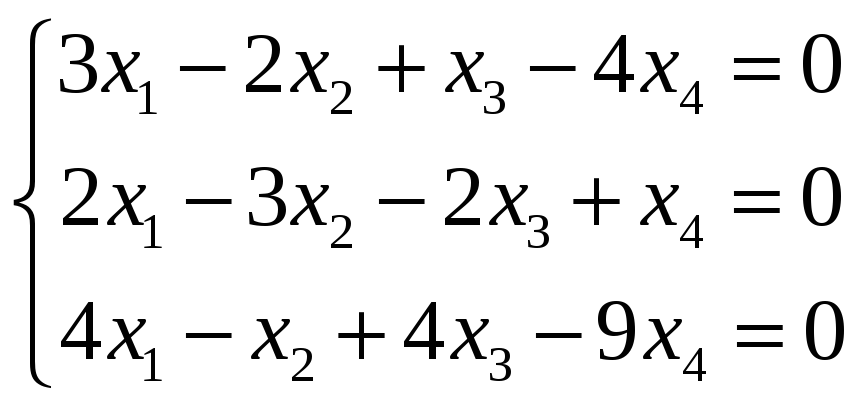
Решение
Найдем ранг матрицы системы уравнений при помощи элементарных преобразований:
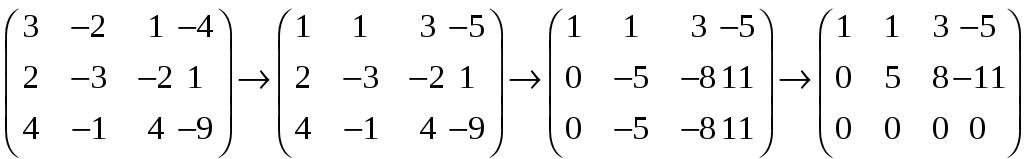 =>
rA=2
=>
rA=2
Значит, система имеет ненулевые решения, размерность пространства которых равна n-r=4-2=2, где n - число неизвестных.
Полученная матрица эквивалента следующей системе
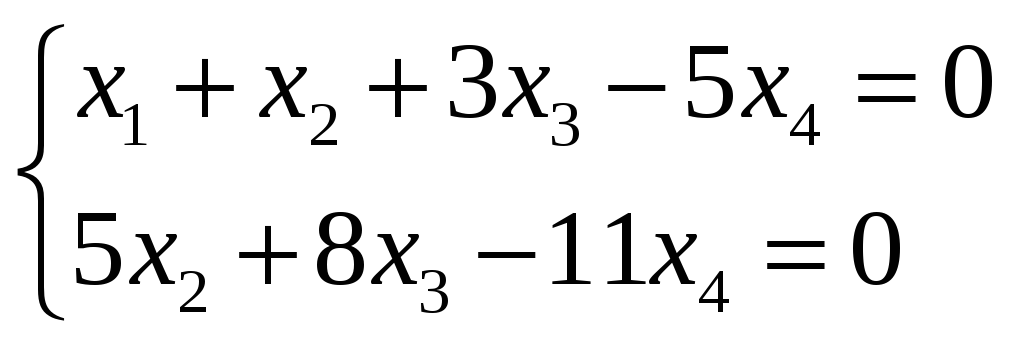 ,
,
откуда


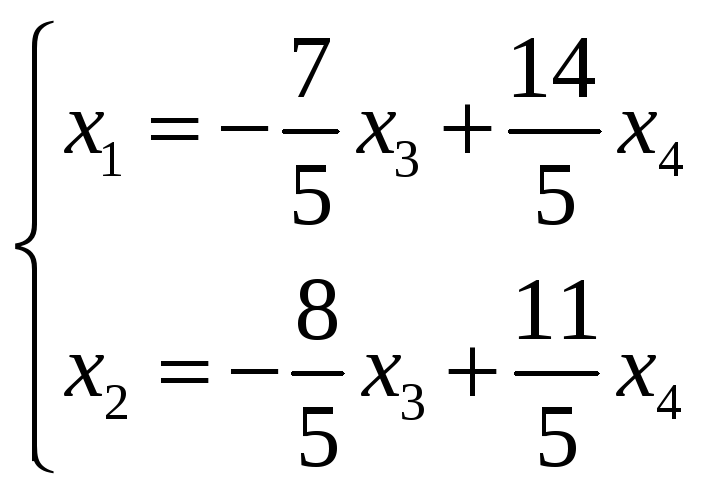 -
общее решение системы.
-
общее решение системы.
Представим его в матричном виде
X= ,
где х3 и х4
,
где х3 и х4![]() .
.
Вектор-столбцы
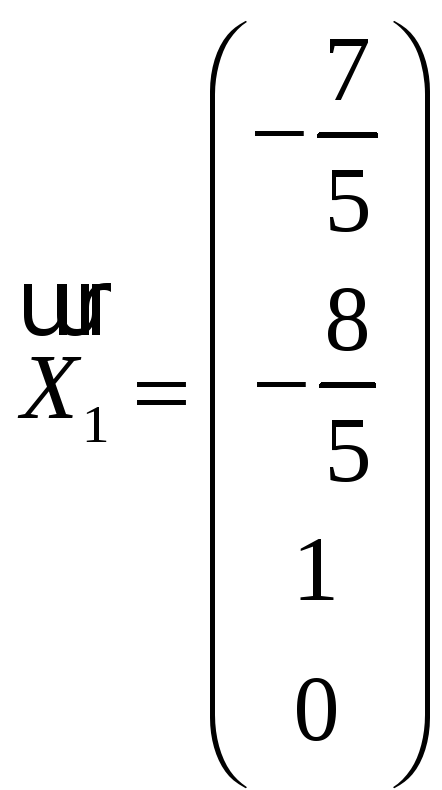 и
и
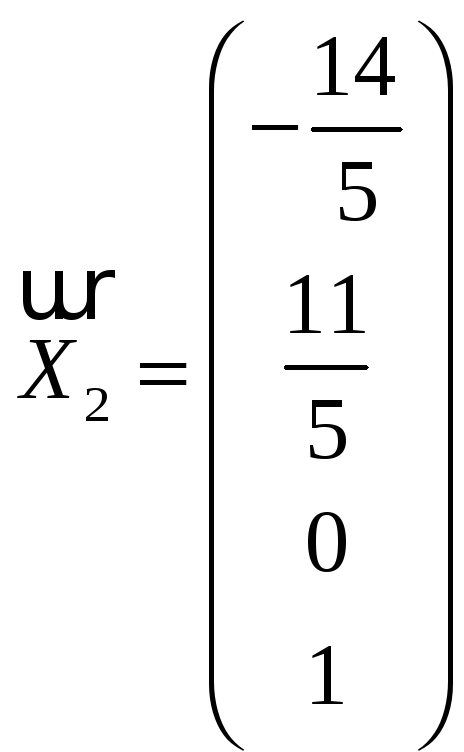 образуют
базис пространства решений системы.
образуют
базис пространства решений системы.
Обозначим х3=С1 , х4=С2, где С1 иС2 –произвольные постоянные. Тогда решение системы в векторном виде примет вид
![]()
Ответ: n-r=2 – размерность пространства решений,
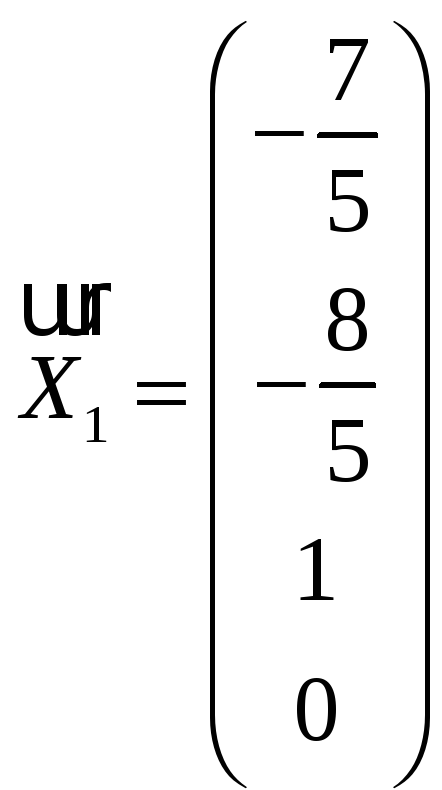 ,
,
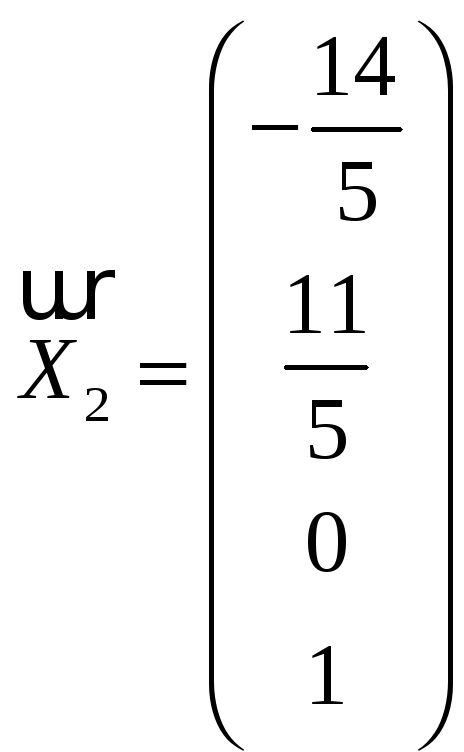 –
базис пространства решений.
–
базис пространства решений.
№52
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.
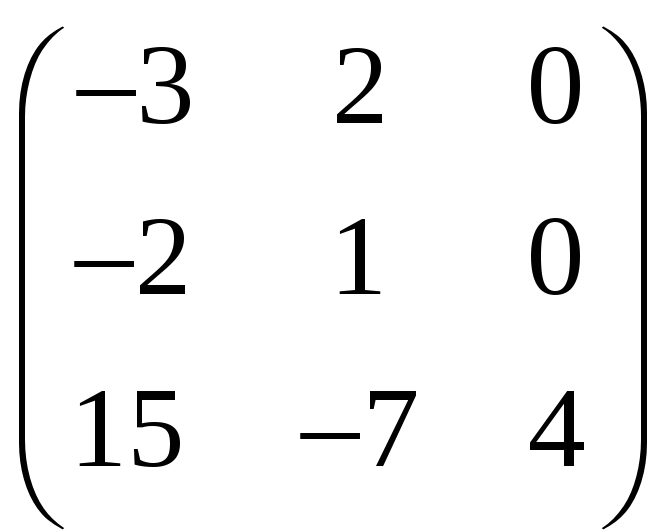
Решение
Составим характеристическое уравнение
матрицы
![]() :
:
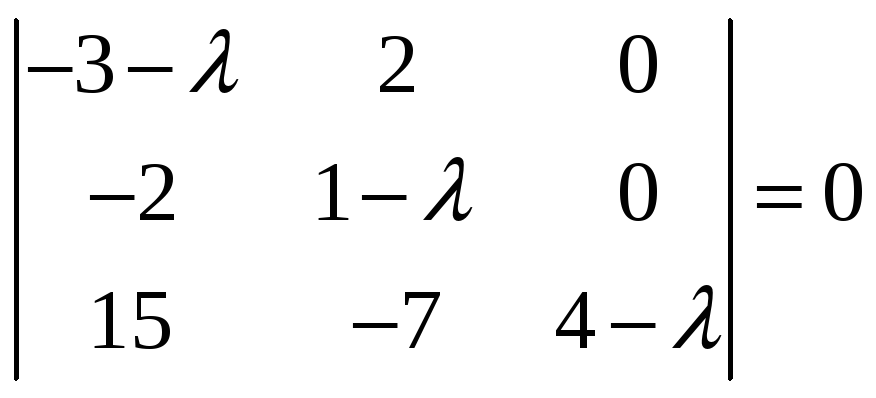
![]()
![]()
![]()
λ1=4, λ2=λ3=-1 – собственные значения матрицы А
Найдем собственные векторы, соответствующие данным собственным значениям, из системы
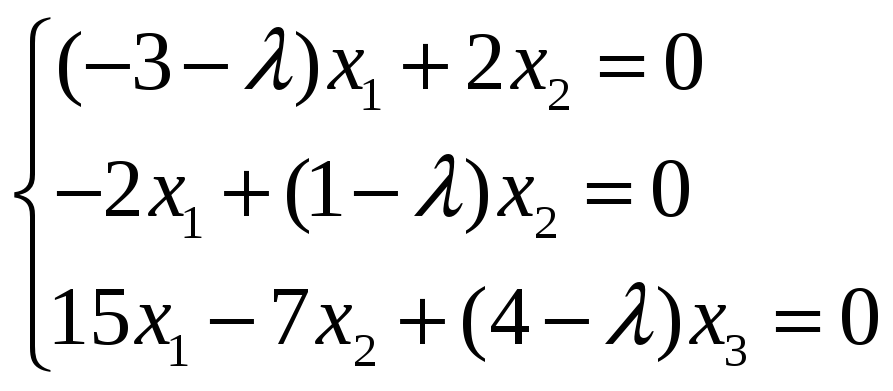
При λ1=4 получим
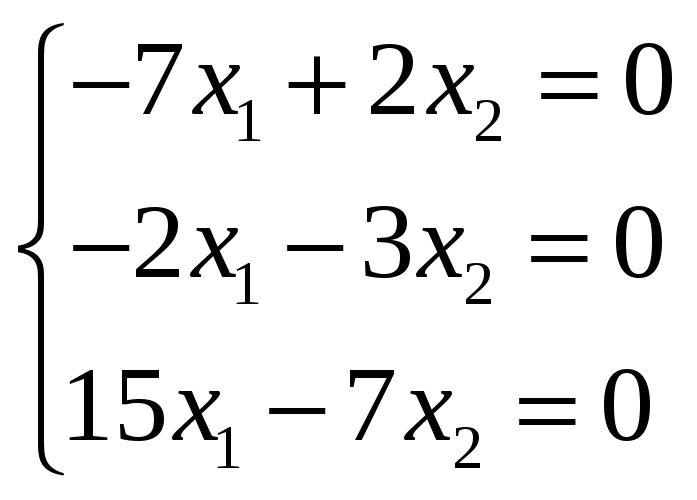 =>
x1=0,
x2=0
=>
x1=0,
x2=0
при х3=1, получим собственный вектор
![]() =(0;0;1)Т
=(0;0;1)Т
При λ1=λ2=-1 получим
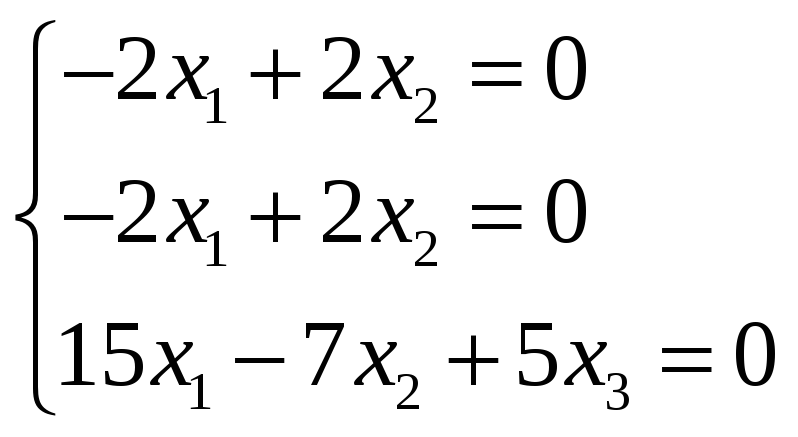
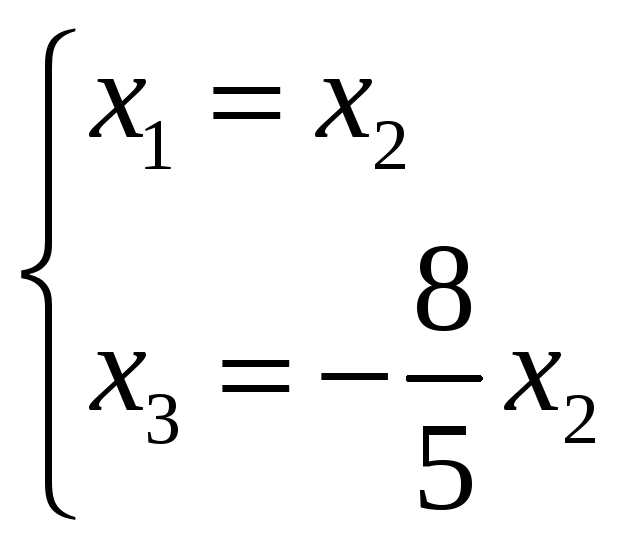
при х2=5, получим собственные
векторы
![]() =
=![]() =(5;5;-8)Т
=(5;5;-8)Т
Ответ: λ1=4, λ2=λ3=-1 – собственные значения,
![]() =(0;0;1)Т
=(0;0;1)Т![]() =
=![]() =(5;5;-8)Т(
с точностью до постоянного множителя)
– собственные векторы.
=(5;5;-8)Т(
с точностью до постоянного множителя)
– собственные векторы.
№62
Привести к каноническому виду уравнение линии второго порядка, используя теорию квадратичных форм.
![]()
Решение
Матрица данной квадратичной формы имеет вид:
А=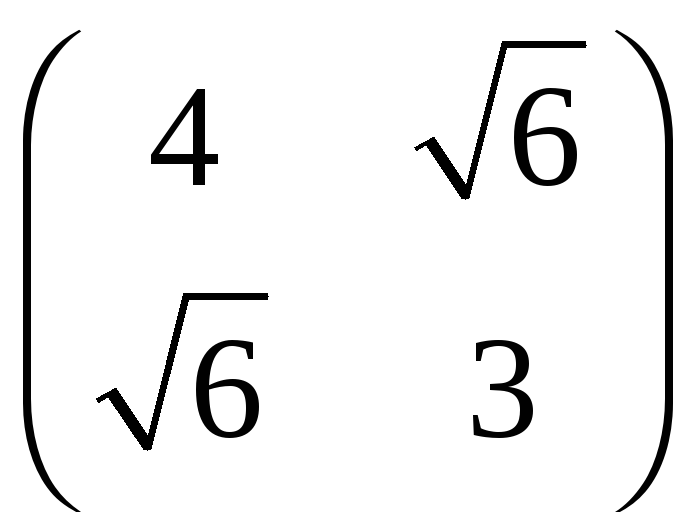
Решим характеристическое уравнение:
![]()

(4-λ) (3-λ)-6=0
![]()
λ1=1, λ2=6 – собственные значения матрицы А.
Найдем собственные векторы из системы

При λ1=1 получим
 =>
x2=
=>
x2=![]() x1
x1
При x1= 2
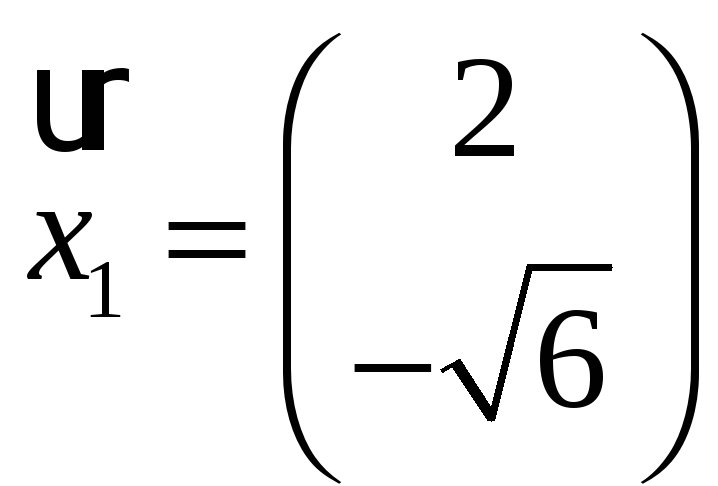
При λ2=6 получим
 =>
x1=
=>
x1=![]() x2
x2
При x2= 2 получим
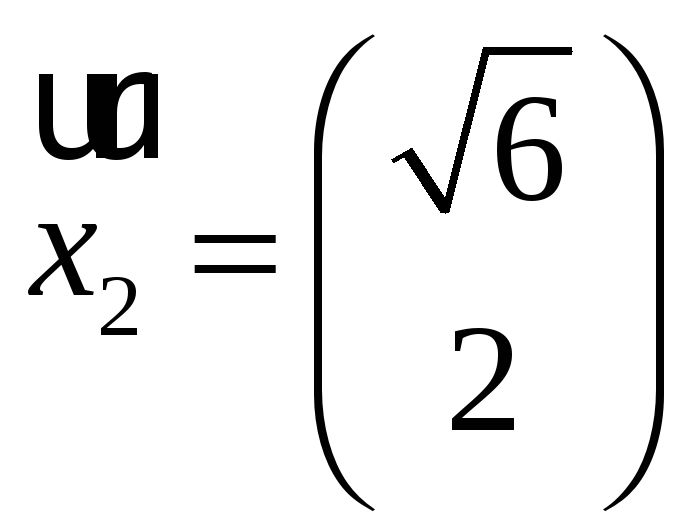
Нормируем собственные векторы:
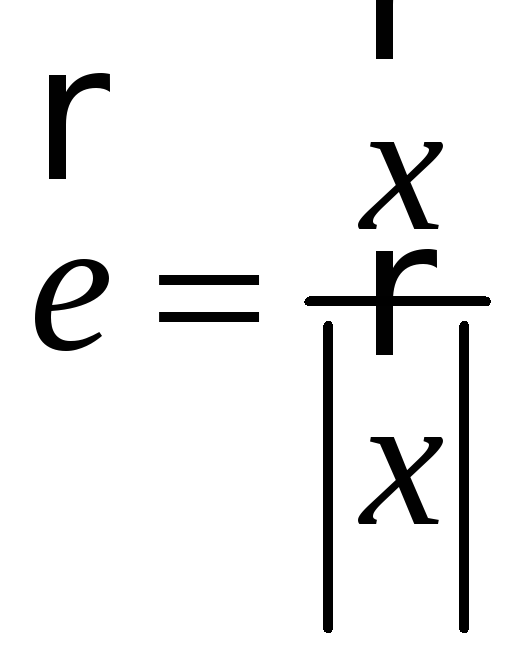
![]()
![]()
Составим матрицу перехода от старого базиса к новому:
T=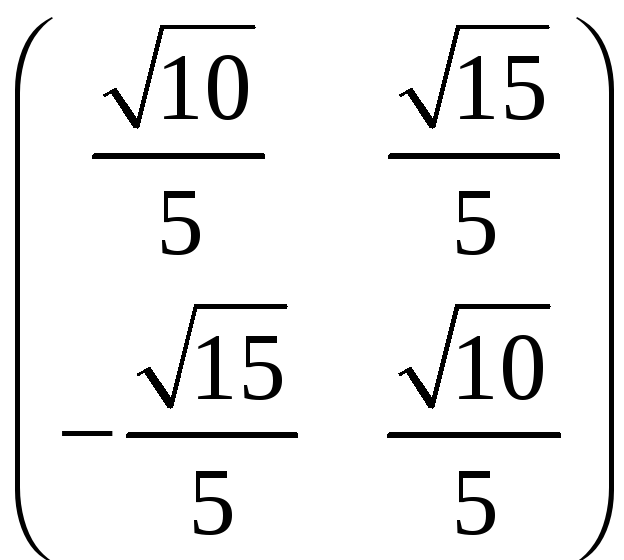
Выполняя преобразование
 ,
получим
,
получим
x=![]()
y=![]()
Подставив данные формулы в исходное уравнение кривой, получим:
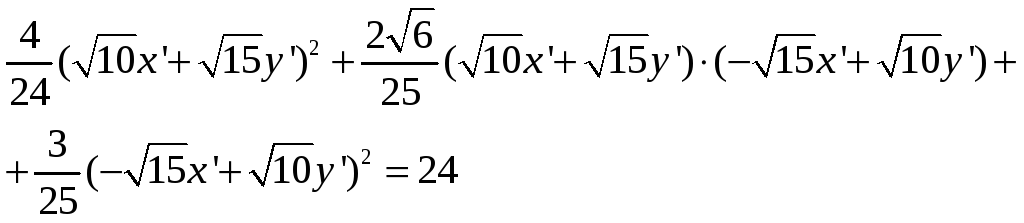
Получим
![]()
Приведем уравнение к каноническому виду
![]() –
каноническое уравнение эллипса с
полуосями а=
–
каноническое уравнение эллипса с
полуосями а=![]() ,
b=2.
,
b=2.
Ответ:
![]()
