Котрольная 8, вариант 5

385.) Вычислить криволинейный интеграл вдоль треугольника с вершинами А(-2, 0), В (2, 0), D (0, 2), обходя его против хода часовой стрелки.

Решение:

Уравнение кривой на промежутке AB

1) , на этом отрезке при этом .

Вычислим интеграл

Уравнение кривой на промежутке BD

2) , при этом x меняется от 2 до 0.

Вычислим интеграл

Уравнение кривой на промежутке DA

3) , при этом x меняется от 0 до -2

Вычислим интеграл

Так как контур интегрирования состоит из трех отрезков АВ, ВD, DА, то

395.) Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Данное тело и его проекцию на плоскость хОу изобразить на чертежах.

z = 0, z = 2 – x,

Решение

Надо вычислить интеграл

Сделаем чертеж

Тело ограничено плоскостями

Отсюда

Область D в плоскости xOy есть область, ограниченная сверху кривой , снизу кривой и с боку прямой

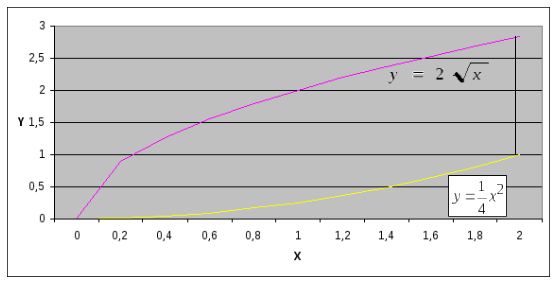
Здесь х изменяется от 0 до 2,

у изменяется от нижней кривой до верхней . Поэтому, расставив пределы интегрирования, получим

405.) Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах. Параметр а положителен.

Решение:

Запишем уравнение кривой в полярных координатах :

Так как , ,откуда следует, что

.

Так как

Продолжим

415.) Найти массу тела, ограниченного координатными плоскостями и плоскостью х + у + z = 1, если плотность в каждой точке численно равна произведению координат этой точки.

Решение:

Для данной фигуры , , , а плотность исходя из условия

Найдем массу фигуры с учетам данной плотности:

425.) Вычислить поток векторного поля F через плоскость треугольника , вырезанного из плоскости (р) координатными плоскостями, в том направлении нормали к плоскости, которая образует с осью Оz острый угол.

F = (2x - z) i + (y - x) j + (x + 2z) k; (p) :x - y + z – 2 = 0

Решение:

Поток единичных нормалей к поверхности, заданной уравнением

, определяется уравнением

В данном случае и, следовательно,

, учитывая, то нормали должны образовывать острый угол с осью OZ, т.е.

, выбираем в этой формуле знак плюс.

Имеем

, находим скалярное произведение

Поток определяется поверхностным интегралом

Переходим от поверхностного интеграла к двойному, проецируя на плоскость XOY:

Определим предварительно границы

Ее проекцию D на плоскость XOY находим исключая z из условий

Отсюда

435.) Проверить, будет ли потенциальным и соленоидальным поле F . В случае потенциальности поля найти его потенциал U (x, y, z).

F = ( 2x - 3yz) i + (2y - 3xz) j + (2z - 3xy) k

Решение:

Найдем по формуле

Поле является потенциальным так как равен 0 во всех точках области V.

Найдем потенциал поля:

Для вычисления потенциала по формуле в качестве точки возьмем начало координат. Тогда получаем

Проверим соленоидальность поля, вычислив

.

Значит, поле не является соленоидальным.