кр 2,вариант 9

Контрольная работа № 2

по дисциплине

«Высшая математика»

вариант 9

Задание 79

Построить график функции у = 3cos(x + 1) преобразованием графика функции y = cos x.

Решение

Строим график функции y = cos x, затем строим график функции y = cos x растяжением y = cos x в раз от оси Оу. График y = cos(x + 1) = cos (x +2) получается параллельным переносом графика y = cos x в отрицательном направлении оси Ох на 2. Растяжением в 3 раза вдоль оси Оу графика y = y = cos(x + 1) получаем график функции у = 3 cos(x + 1).

Изобразим соответствующие графики:

y = 3cos (x + 1)

y = cos (x + 1)

y = cos x

y = cos x

Задание 89

Дана функция r = на отрезке 0 £ φ £ 2π. Требуется: 1) построить график функции в полярной системе координат по точкам, давая j значения через промежуток p/8, начиная от j = 0; 2) найти уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, и по уравнению определить, какая это будет линия.

Решение

1) Полярному углу φ будем придавать значения от угла φ = 0 до φ = 2π через промежуток π/8 и вычислять соответствующие значения полярного радиуса r. Результаты запишем в таблицу:

φ	r =
0	< 0
π/8	< 0
π /4	< 0
3π/8	25,572
π/2	6
5π/8	3,399
3π/4	2,485
7π/8	2,107
π	2
9π/8	2,107
5π/4	2,485
11π/8	3,399
3π/2	6
13π/8	25,572
7π/4	< 0
15π/8	< 0
2π	< 0

При φ → ; r → ¥; при φ Î и φ Î точек линии нет, так как не может быть r < 0. Для вычерчивания линии проведем радиусы-векторы, соответствующие углам φ, взятым с интервалом π/8. На каждом из этих радиусов-векторов откладываем отрезки, равные значению r при соответствующем значении φ из таблицы. Соединим эти точки плавной линией и получим изображение кривой.

Сделаем чертеж:

2) Найдем уравнение этой кривой в декартовых координатах. Для этого подставим в исходное уравнение r = , cos φ = .

Получим: = .

Преобразуем это соотношение: = ;

– 2x = 6; = 6 + 2x.

Возведем обе части равенства в квадрат:

х² + у² = (6 + 2x)²; х² + у² = 36 + 24x + 4x²;

3х² – у² + 24x + 36 = 0

3(х² + 8x + 16 – 16) – у² + 36 = 0

3(х + 4)² – 48 – у² + 36 = 0

3(х + 4)² – у² = 12

– = 1.

Полученное уравнение есть уравнение ветви гиперболы с полуосями а = 2, b = 2 с центром в точке А(–4; 0).

Задание 99

Найти указанные пределы, не пользуясь правилом Лопиталя.

a) ; б) ;

в) ; г) .

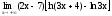Решение

a) .

Подстановка предельного значения аргумента приводит к неопределенности . Разделим числитель и знаменатель на старшую степень аргумента, т.е. на x³. Получим

,

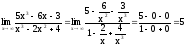так как при , , и – бесконечно малые функции.

б) .

Непосредственная подстановка аргумента х = 5 приводит к неопределенности вида . Избавимся от иррациональности в числителе, домножив числитель и знаменатель на , а знаменатель разложим на множители по формуле:

ax² + bx + c = a(x – x₁)(x – x₂), где х₁, x₂ – корни уравнения ax² + bx + c = 0

2х² – 7х – 15 = 0;

D = 49 + 120 = 169;

x₁ = (7 – 13) / 4 = –, x₂ = (7 + 13) / 4 =5.

3х² + 4х + 1 = 2(x – 5)(x + ) = (x – 5)(2x + 3).

()() = 2х + 1 – х – 6 = х – 5.

Тогда:

=

в) .

Подстановка предельного значения аргумента х = 0 приводит к неопределенности вида 0 · ¥. Применяем сначала формулу тригонометрии: ctg 5x = , а затем воспользуемся первым замечательным пределом .

=

г) .

При х → +¥ имеем неопределенность вида ¥ · (¥ – ¥), которую преобразуем, используя свойство логарифмической функции:

(2х – 7) · [ln(3x + 4) – ln 3x ] = (2х – 7) · ln = ln= ln.

Тогда,

== [имеем неопределенность вида 1^¥, раскроем ее с помощью 2-го замечательного предела ] =

= =

= = .

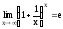Задание 109

Заданы функция у = f(x) = и два значения аргумента х₁ = 6 и х₂ = 2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы при приближении к точке разрыва слева и справа; 3) сделать схематический чертеж.

Решение

1) Так f(x) является элементарной функцией, то она непрерывна во всех точках, в которых определена. Следовательно, в точке х₁ = 6 функция непрерывна, а в точке х₂ = 2 она не является непрерывной (деление на ноль неопределенно). Значит, х₂ = 2 – точка разрыва функции.

2) Вычислим односторонние пределы в точке х₂ = 2:

Один из пределов оказался бесконечным, поэтому х₂ = 2 – точка разрыва 2-го рода.

3) Учитывая, что , строим схематический график функции.

y = 1

x = 2

Задание 119

Задана функция y = 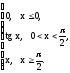различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать чертеж.

Решение

Функция y =0 непрерывна на (–¥; 0], функция y = tg x непрерывна на (0; ), а y =x – непрерывна на [; +¥), значит f(x) непрерывна на интервалах (–¥; 0)(0; ) (; +¥).

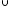Исследуем поведение функции в точках х₁ = 0 и х₂ = . Находим правые и левые пределы функции в этих точках.

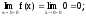
; f(0) = 0.

Так как f(0) = 0, то f(x) в точке x₁ = 0 непрерывна.

; f() = , т.е. х₂ = 2 – точка разрыва 2‑го рода, так как = +

Сделаем чертеж:

x = π/2