Высшая математика 9 вариант

ВАРИАНТ 9

Контрольная работа № 1.

Основы векторной алгебры и аналитической геометрии

Задачи 1–10

Даны четыре вектора , , и , в некотором базисе. Показать, что векторы образуют базис и найти координаты вектора в этом базисе.

Решение

3) Найдем смешанное произведение векторов

–32 0.

Значит, векторы некомпланарны и образуют базис.

Составим систему уравнений в координатном виде , где координаты вектора в базисе , и найдем .

Определитель найден выше: .

, ;

Имеем: , ; .

Значит, .

Задачи 11–20

Даны координаты вершин пирамиды . Найти: 1) длину ребра ; 2) угол между рёбрами и ; 3) угол между ребром и гранью ; 4) площадь грани ; 5) объём пирамиды; 6) уравнение прямой ; 7) уравнение плоскости ; 8) уравнение высоты, опущенной из вершины на грань ; 9) сделать чертёж.

Решение

1) Длина ребра численно равна расстоянию между точками и , которое в декартовой системе координат вычисляется по формуле

,

где координаты точки , координаты точки .

Таким образом, вычисляем:

.

2) Угол  между ребрами и вычисляется по формуле из скалярного произведения векторов и .

Найдем координаты векторов и .

= .

=.

Тогда = =.

.

3) Угол  между ребром и плоскостью – это угол между вектором и его ортогональной проекцией на грань .

Вектор перпендикулярен грани , что вытекает из определения векторного произведения векторов и

Вектор перпендикулярен грани , что вытекает из определения векторного произведения векторов и

== .

Тогда == = .

4) Площадь грани находим, используя геометрический смысл векторного произведения:

Тогда = .

= .

5) Объем пирамиды численно равен одной шестой модуля смешанного произведения векторов , , , которое находится по формуле .

== –53.

Значит, =.

6) Для составления уравнений прямой воспользуемся формулой: , где координаты точки , координаты точки .

Получим: = = – канонические уравнения прямой .

7) Для составления уравнения плоскости воспользуемся формулой , где координаты точки , координаты точки , координаты точки .

=.

=0 – уравнение плоскости.

8) Искомое уравнение высоты получим из канонических уравнений прямой , где точка, лежащая на искомой прямой; координаты вектора , параллельного искомой прямой. При этом в качестве точки возьмем точку , а в качестве вектора возьмем нормальный вектор плоскости , т.е. = (–4, –11, –3).

Имеем .

9) Сделаем чертёж:

Задача 29. Составить уравнение линии, каждая точка которой отстоит от точки А(4;0) вдвое дальше, чем от прямой .

Решение

Обозначим произвольную точку искомой кривой как . Тогда по условию получаем, что , где Р – основание перпендикуляра из точки М к прямой .

Находим: ; .

Значит, . Возводя обе части этого соотношения в квадрат, получаем , ,

Это каноническое уравнение гиперболы с центром в точке (0, 0), действительная полуось , мнимая полуось .

Задачи 31–40

Доказать совместность данной системы линейных уравнений и решить её тремя методами: 1) по формулам Крамера; 2) средствами матричного исчисления (с помощью обратной матрицы).

Задача 39: 

Решение

Докажем совместность системы.

Найдем ранг основной и расширенной матрицы системы

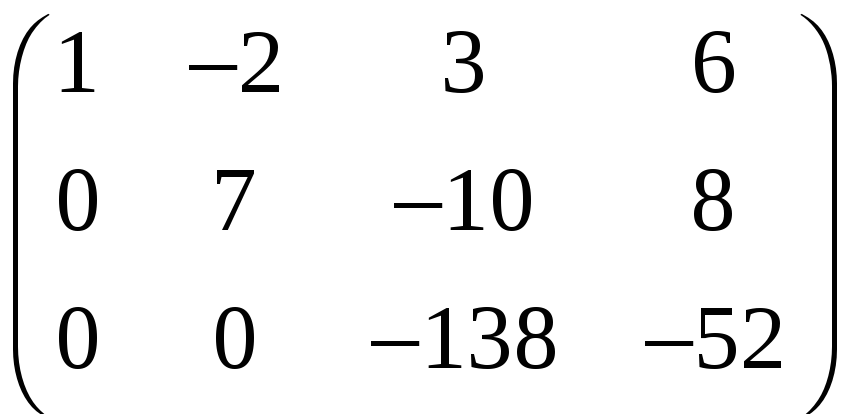
Ранг основной матрицы равен рангу расширенной матрицы и равен количеству неизвестных , следовательно, система совместна и определена.

Найдем решение системы с помощью формул Крамера. Воспользуемся формулами Крамера:

, , , где – определитель, составленный из коэффициентов при неизвестных.

== –15–12+24–27–8–20= –58;

= –464; = –232; = –116

Найдем , , .

Получим (8, 4, 2) – решение системы.

2. Решим систему матричным способом. Запишем систему в матричной форме ,

где , , .

Решение системы в матричной форме имеет вид , где – матрица, обратная матрице . Найдем матрицу по формуле

= , где = –58 , – алгебраическое дополнение к элементу.

=	=	=
=	=	=
=	=	=

Обратная матрица имеет вид: =.

Найдем решение системы.

== =.

(8, 4, 2) – решение системы.

Ответ: (8, 4, 2).

Задачи 41–51

Найти базис и размерность решений однородной системы линейных уравнений.

Задача 49:

Решение

Матрица, из коэффициентов системы

Получили трапециевидную матрицу, следовательно, система совместна и не определена.

Видно, что ранг матрицы равен 2. Следовательно, 2 неизвестные являются главными, а 2 - свободными. Значит, фундаментальная система решений системы содержит 4–2= 2 линейно независимое решение. Выберем в качестве главных неизвестных .

Система, соответствующая преобразованной матрице, имеет вид

.

Или иначе:

.

Фундаментальная совокупность решений, является базисом линейного пространства решений исходной системы. Следуя общему правилу, полагаем ; затем – . В результате приходим к двум частным решениям, которые и составляют фундаментальный набор.

; .

Размерность искомого пространства равна 2.

Все решения данной системы выражаются через фундаментальный набор:

, где произвольные числа.

Ответ: .

Задачи 51–60

Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей.

Задача 59: 

Решение.

Составляем характеристическое уравнение матрицы А и находим его корни:

.

= 0, .

Так как все корни оказались действительными числами, то они являются собственными значениями матрицы А.

При система имеет вид:

Значит, собственному значению соответствует собственный вектор

.

Здесь х₃ – произвольное действительное число, не равное нулю. Положив его, в частности, равным единице, получим собственный вектор в виде

Аналогично при система имеет вид:

Значит, собственному значению соответствует собственный вектор

.

Здесь х₂ – произвольное действительное число, не равное нулю. Соответствующий собственный вектор имеет вид .

Таким образом, матрица А имеет три собственных значения

, а нормированные собственные векторы имеют вид

, .

Задачи 61–70

Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка.

Задача 69: .

Решение.

Составим матрицу данной квадратичной формы и найдём её собственные значения: .

Корнями характеристического уравнения являются числа и .

При система имеет вид:

Значит, собственному значению соответствует собственный вектор

.

Положив его, в частности, равным единице, получим собственный вектор в виде

Аналогично при система имеет вид:

Значит, собственному значению соответствует собственный вектор

.

Соответствующий собственный вектор имеет вид .

Нормируя собственные векторы, получим

и .

Матрица перехода Т к новому базису имеет вид .

Вводим замену переменных

Подставим эти выражения в исходное уравнение кривой: